目录
方法一:多项式特征(Polynomial Features)
方法二:交互特征(Interaction Features)
方法三:基函数扩展(Basis Function Expansion)
高斯径向基核函数(Gaussian Radial Basis Function, RBF)
支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用)
在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
线性SVM依赖数据表达的距离测度,所以需要对数据先做normalization,LR不受其影响
一、深度学习面试宝典
深度学习八股https://github.com/nxpeng9235/MachineLearningFAQ
1、逻辑回归(LR)
"对数几率回归"
知识点提炼
- 分类,经典的二分类算法!
- 逻辑回归就是这样的一个过程:面对一个回归或者分类问题,建立代价函数,然后通过优化方法迭代求解出最优的模型参数,然后测试验证我们这个求解的模型的好坏。
- Logistic 回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别)
- 回归模型中,y 是一个定性变量,比如 y = 0 或 1,logistic 方法主要应用于研究某些事件发生的概率。
- 逻辑回归的本质:极大似然估计
- 逻辑回归的激活函数:Sigmoid
- 逻辑回归的代价函数:交叉熵
逻辑回归的优缺点
优点:
1)速度快,适合二分类问题
2)简单易于理解,直接看到各个特征的权重
3)能容易地更新模型吸收新的数据
缺点:
对数据和场景的适应能力有局限性,不如决策树算法适应性那么强
逻辑回归中最核心的概念是 Sigmoid 函数,Sigmoid函数可以看成逻辑回归的激活函数。
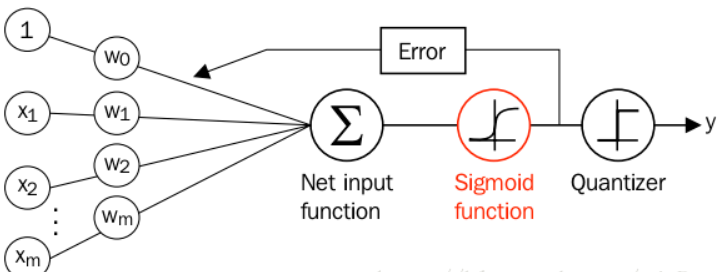
Sigmoid
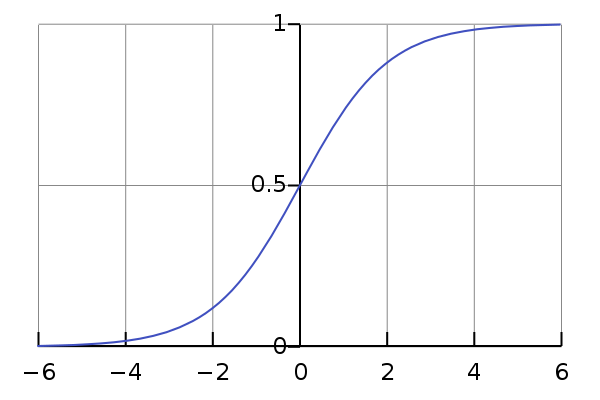
- Sigmoid函数的输出范围是 0 到 1。这是因为无论输入 x 的值多大或多小,函数的分母
总是大于 1,因此值总是介于 0 和 1之间。
- Sigmoid函数的导数非常重要,因为在训练神经网络时需要计算梯度。Sigmoid函数的导数是:
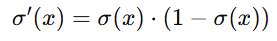
-
优缺点
- 优点:Sigmoid函数将输入值压缩到 000 和 111 之间,非常适合用于二分类问题的输出层。
- 缺点:当输入值非常大或非常小时,函数的梯度会趋近于零,导致梯度消失问题。这使得深层神经网络的训练变得困难。
为什么 LR 要使用 sigmoid 函数
1. 将输出值限制在 [0, 1] 区间
逻辑回归的目标是进行二分类,即将输入分类到两个类别之一。Sigmoid 函数可以将任意实数输入转换为 [0, 1] 之间的概率值,这非常适合表示一个事件发生的概率。例如,输出 0.8 表示分类器认为某个输入属于类别 1 的概率是 80%。
2. 解释为概率
Sigmoid 函数的输出可以自然地解释为某个事件发生的概率,这使得逻辑回归模型的输出更加直观和易于理解。对于二分类问题,输出值接近 1 表示高概率属于正类,接近 0 表示高概率属于负类。
3. 导数的计算和梯度下降
Sigmoid 函数的导数有一个简洁的形式:
这种形式使得在计算梯度时非常方便,特别是使用梯度下降法来优化逻辑回归模型的参数时。导数的形式简化了计算过程,提高了训练效率。
4. 非线性变换
逻辑回归使用 Sigmoid 函数将线性模型的输出(即线性回归的结果)转换为非线性结果。这意味着逻辑回归能够处理一些线性不可分的数据,使得模型能够捕捉到更复杂的数据关系。
5. 理论基础
逻辑回归基于对数几率(log-odds)的概念。对于某个输入 xxx,逻辑回归模型计算线性组合 ![]() ,然后应用 Sigmoid 函数将其转换为概率:
,然后应用 Sigmoid 函数将其转换为概率:
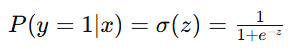
这种基于对数几率的模型有坚实的统计学基础,使得逻辑回归模型在概率解释上有很强的理论支持。
6. 损失函数的凸性
逻辑回归通常使用交叉熵损失函数(log loss),这种损失函数在使用 Sigmoid 激活函数时具有良好的凸性。这意味着在优化过程中容易找到全局最优解,训练过程更稳定。
总结来说,逻辑回归使用 Sigmoid 函数是因为它可以将输出值限制在 [0, 1] 区间,方便解释为概率,简化导数计算,提供非线性变换,并且有坚实的理论基础和优化优势。
交叉熵损失函数
即对数损失函数。能够有效避免梯度消失.

二分类问题中的交叉熵损失
对于二分类问题,目标是预测一个样本属于正类(类1)的概率 ![]() ,给定实际标签 y(0 或 1)。交叉熵损失函数的公式如下:
,给定实际标签 y(0 或 1)。交叉熵损失函数的公式如下:
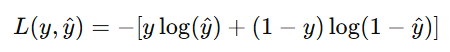
直观理解:
- 当实际标签 y为 1 时,损失函数主要关注
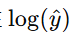 。如果预测的概率
。如果预测的概率 越接近 1,损失越小;如果预测的概率
越接近 0,损失越大。
- 当实际标签 y 为 0 时,损失函数主要关注
。如果预测的概率
越接近 1,损失越小;如果预测的概率
越接近 0,损失越大。
多分类问题中的交叉熵损失
对于多分类问题(假设有 C 个类别),交叉熵损失的公式如下:
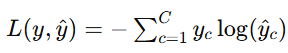
损失函数反向传播推导
摘自 线性回归和逻辑回归的比较_逻辑回归和线性回归相同点-CSDN博客
损失函数的由来:
已知估计函数为:
![]()
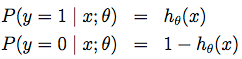
![]()
由最大似然估计原理,我们可以通过m个训练样本值,来估计出值,使得似然函数值(所有样本的似然函数之积)最大
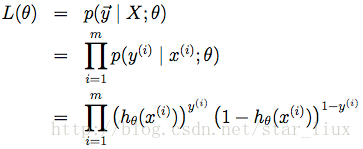

为什么 LR 用交叉熵损失而不是平方损失?
1. 概率解释和性质
- 概率输出:逻辑回归的目标是预测概率值,表示某个事件发生的可能性。交叉熵损失函数直接衡量预测的概率分布和实际的分布之间的差异,这与逻辑回归的目标一致。平方损失函数通常用于回归问题,预测连续值,而不是概率。
2. 凸性和优化
- 凸性:交叉熵损失函数对于逻辑回归是一个凸函数,这意味着它只有一个全局最优解,使用梯度下降等优化算法可以有效地找到最优解。而平方损失在逻辑回归中可能不是凸函数,可能会有多个局部最优解,使得优化过程不稳定。
3. 梯度的性质
- 梯度的梯度消失问题:在逻辑回归中使用 Sigmoid 函数时,交叉熵损失函数的梯度与输入相关性更好。平方损失函数的梯度在 Sigmoid 函数输出接近 0 或 1 时会变得非常小,这会导致梯度消失问题,使得训练过程非常缓慢或无法收敛。
4. 损失函数的合适性
- 针对分类问题的设计:交叉熵损失函数专门设计用于分类问题。它会对错误分类的预测进行更大的惩罚,特别是在预测概率与实际标签差距较大时,这有助于提高分类模型的性能。而平方损失函数对误差的处理是对称的,不区分分类错误的严重程度,因此不适合分类任务。
示例说明
假设我们有一个二分类问题,真实标签 y=1y = 1y=1,模型预测的概率 y^\hat{y}y^ 分别为 0.9 和 0.1 时,使用交叉熵损失和平方损失的对比:
交叉熵损失:
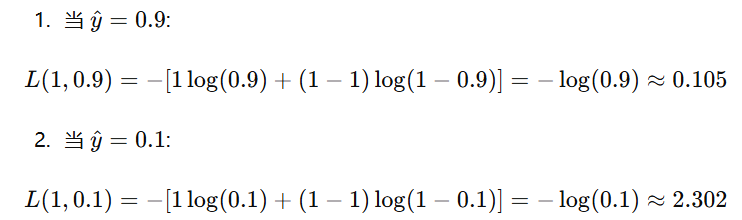
平方损失:
逻辑回归使用交叉熵损失而不是平方损失,主要是因为交叉熵损失更适合概率输出的解释,更容易优化(凸性),可以避免梯度消失问题,并且对错误分类有更大的惩罚,从而提高分类模型的性能。
LR 能否解决非线性分类问题?
逻辑回归(Logistic Regression, LR)本质上是一个线性分类器,因此在处理复杂的非线性分类问题时,其能力是有限的。不过,通过一些扩展和技巧,可以增强逻辑回归的非线性分类能力。
1. 基本逻辑回归的局限性
基本的逻辑回归模型是线性的,它通过寻找一个线性决策边界来区分两个类别。如果数据集中的分类边界是非线性的,基本的逻辑回归模型可能无法很好地拟合数据,导致分类性能较差。
2. 增强逻辑回归非线性分类能力的方法
方法一:多项式特征(Polynomial Features)
通过增加输入特征的多项式项,可以将原始特征空间映射到更高维的空间,使得模型可以拟合非线性的决策边界。例如,对于二维输入特征 x1 和 x2,可以扩展成以下多项式特征:
![]()
使用这些多项式特征进行逻辑回归,可以捕捉到数据中的非线性关系。
方法二:交互特征(Interaction Features)
交互特征是指两个或多个特征的组合,例如![]() 。这些特征可以帮助模型捕捉不同特征之间的交互作用,从而更好地处理非线性分类问题。
。这些特征可以帮助模型捕捉不同特征之间的交互作用,从而更好地处理非线性分类问题。
方法三:基函数扩展(Basis Function Expansion)
基函数扩展通过使用一些非线性函数(如高斯基函数、多项式基函数等)将原始特征映射到新的特征空间。例如,高斯基函数:![]()
方法四:核方法(Kernel Trick)
核方法是支持向量机(SVM)中常用的一种技巧,但也可以应用于逻辑回归。核方法通过隐式地将输入特征映射到高维空间,而无需显式地计算这些高维特征。常见的核函数有线性核、径向基函数(RBF)核和多项式核。
虽然基本的逻辑回归模型是线性分类器,但通过扩展特征空间的方法,如多项式特征、交互特征、基函数扩展和核方法,可以增强逻辑回归处理非线性分类问题的能力。这些方法在实际应用中非常有效,使得逻辑回归不仅能处理线性分类问题,还能处理一定程度的非线性分类问题
2、线性回归
基本原理
线性回归的基本假设是,自变量和因变量之间存在线性关系,即因变量的期望值可以用自变量的线性组合来表示。这个关系通常用一个线性方程来表示:![]()
线性回归的目标是找到最佳的参数估计值,使得模型的预测值与真实值之间的误差最小化。通常使用最小二乘法来估计参数,即通过最小化观测值与模型预测值之间的残差平方和来确定参数。
在线性回归模型中,输出一般是连续的, 对于每一个输入的x,都有一个对应的输出y。因此模型的定义域和值域都可以是无穷。
举例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 数据
X = np.array([750, 800, 850, 900, 950]).reshape(-1, 1)
y = np.array([150, 180, 200, 220, 240])
# 创建线性回归模型并拟合数据
model = LinearRegression()
model.fit(X, y)
# 预测值
y_pred = model.predict(X)
# 绘图
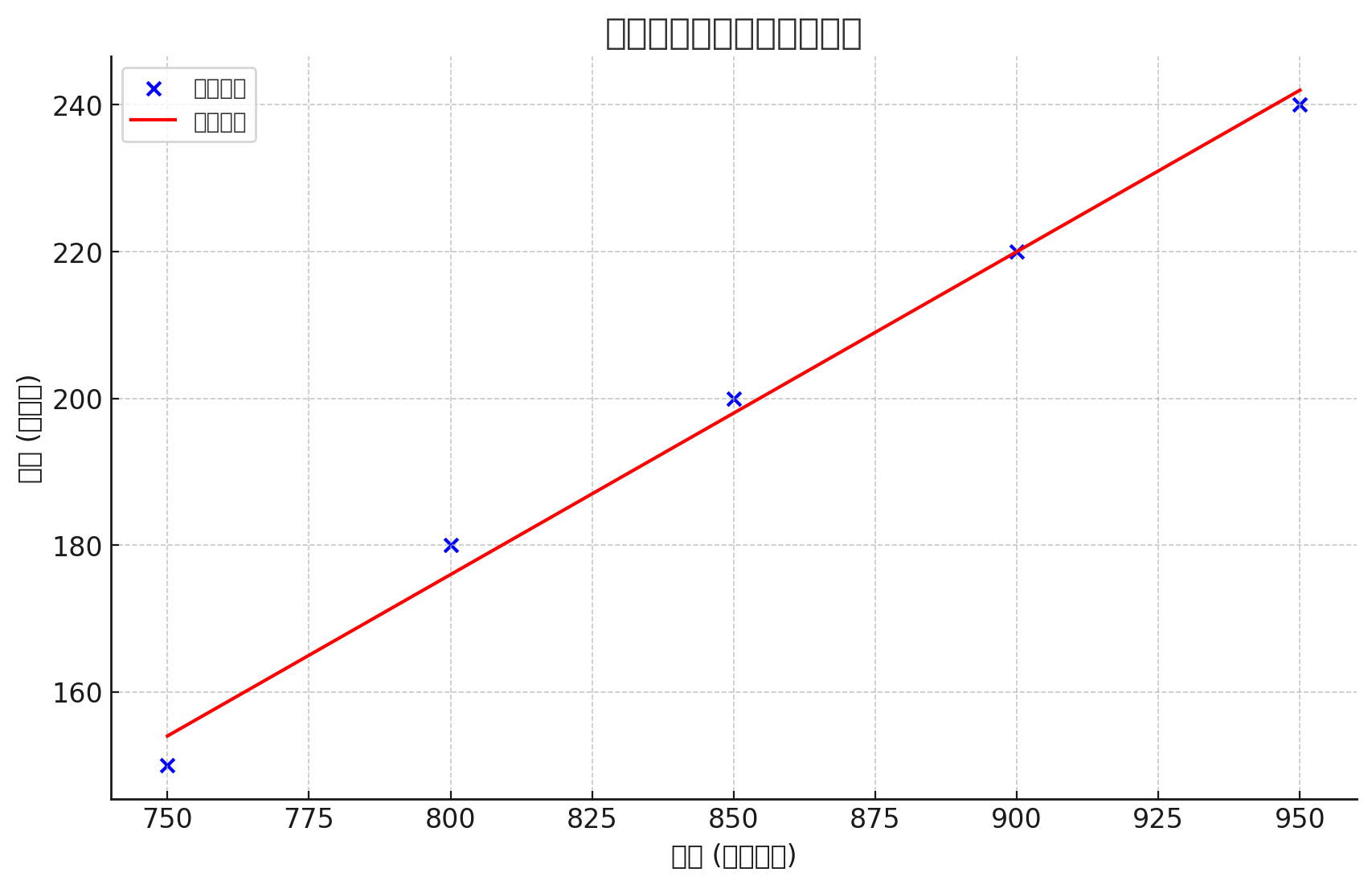
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X, y_pred, color='red', label='回归直线')
plt.xlabel('面积 (平方英尺)')
plt.ylabel('价格 (万美元)')
plt.title('房屋面积与价格的线性回归')
plt.legend()
plt.show()
与逻辑回归(LR)的区别
1. 目标变量的类型
- 线性回归:用于预测连续型变量。也就是说,目标变量 yyy 是一个连续值,比如房价、温度等。
- 逻辑回归:用于分类问题,特别是二分类问题。目标变量 yyy 是一个离散值,通常是0或1,表示两种类别。
2. 模型方程
-
线性回归:模型方程是线性的,即
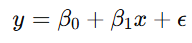
其中 y 是预测的连续值。
-
逻辑回归:模型方程是非线性的,通过逻辑函数(logistic function)将线性方程转化为概率,即
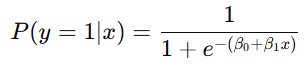
这里,输出是一个概率值,表示样本属于类别1的概率。
3. 损失函数
-
线性回归:最小化均方误差(MSE),即
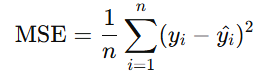
-
逻辑回归:最大化似然函数,通常转化为最小化对数损失(log loss),即
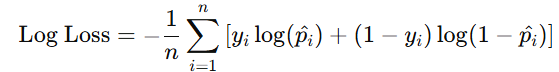
其中,
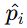 是样本属于类别1的预测概率。
是样本属于类别1的预测概率。
4. 预测输出
- 线性回归:直接预测一个连续值。
- 逻辑回归:预测的是类别的概率值,通过设定一个阈值(通常是0.5)将概率值转化为分类标签。
3、支持向量机(SVM)
基本原理
1. 线性可分性
SVM的目标是找到一个最优超平面将数据分开,尽可能使不同类别的样本点分离。对于二维数据,这个超平面就是一条直线,而对于三维数据,则是一个平面。对于更高维的数据,则是一个超平面。
2. 最大化间隔
SVM通过最大化超平面与各类别样本点之间的最小间隔来找到最优超平面。这个间隔被称为“边界”或“间隔”。最大化间隔可以提高分类器的泛化能力,减少过拟合的风险。
3. 支持向量
在找到的最优超平面上,只有一小部分数据点对确定超平面起关键作用,这些数据点称为“支持向量”。支持向量是离超平面最近的样本点,它们直接影响间隔的大小。
4. 非线性可分性
对于非线性可分的数据,SVM使用核函数(kernel function)将原始数据映射到高维空间,在高维空间中找到一个线性可分的超平面。常用的核函数有线性核、多项式核、高斯径向基核(RBF)等。
5. 损失函数和正则化
SVM通过优化以下目标函数来找到最优超平面:
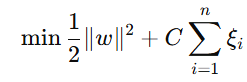
其中,是权重向量的范数,用于最大化间隔;C 是正则化参数,用于控制间隔最大化与误分类惩罚之间的平衡;
是松弛变量,允许部分样本点在间隔内,但要付出惩罚。
SVM分类器的数学表示
对于一个输入向量 xxx,SVM分类器的决策函数为:
![]()
其中,w 是权重向量,b 是偏置项,sign 函数用来确定 x 所属的类别。
当训练数据线性可分时,通过硬间隔最大化(hard margin maximization)学习一个线性的分类器,即线性可分支持向量机,又成为硬间隔支持向量机;
当训练数据近似线性可分时,通过软间隔最大化(soft margin maximization)也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
当训练数据不可分时,通过核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机。
核方法的原理
-
数据映射到高维空间: 核方法通过一个非线性映射函数
 将原始数据从低维空间映射到高维空间:
将原始数据从低维空间映射到高维空间: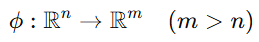
在高维空间中,数据可能变得线性可分。
-
核函数的定义: 核函数
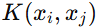 定义为在高维空间中映射后的内积:
定义为在高维空间中映射后的内积: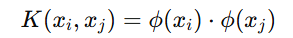
直接计算
 的映射和内积可能非常复杂且计算量大。核函数的引入避免了显式计算高维映射,直接在低维空间计算内积。
的映射和内积可能非常复杂且计算量大。核函数的引入避免了显式计算高维映射,直接在低维空间计算内积。 -
常用的核函数:
-
线性核:
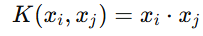
适用于线性可分的数据。
-
多项式核:
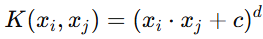
其中 c 是一个常数,d 是多项式的度数。
-
高斯径向基函数(RBF)核:
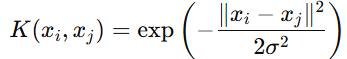
其中 σ 是核函数的带宽参数。RBF核是最常用的核函数之一,适用于大多数非线性情况。
-
Sigmoid核:
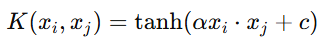
其中 α 和 c 是常数
- 拉普拉斯(Laplac)核函数
-
Sigmoid核函数相关:
这里的符号和参数定义如下:
表示输入向量 x 和 y 的核函数值。
是双曲正切函数,定义为
。
- α 是一个可调的参数,通常称为“增益”参数。
- 〈x,y〉表示 x 和 y 的内积。
- c 是一个偏移量参数。
拉普拉斯核函数
数学表达式为:
其中:
- K(x, y) 是核函数值,表示输入向量 x 和 y 之间的相似度。
是 x 和 y 之间的 L1 距离(曼哈顿距离),即各坐标差的绝对值之和。
- σ 是一个可调参数,控制核函数的“宽度”,σ 越大,函数的衰减速度越慢。
详细解释
距离度量:
- 拉普拉斯核函数使用 L1 距离(曼哈顿距离)来度量 x 和 y 之间的差异。
- L1 距离的公式为:
,其中 xi 和 yi 是向量 x 和 y 的第 i 个分量。
指数衰减:
- 核函数值通过指数衰减函数来计算:
。
- 当 x 和 y 之间的距离增大时,核函数值会快速减小。这个特性使得拉普拉斯核函数能够很好地捕捉局部相似性。
参数 σ:
- σ 控制核函数的宽度,σ 越大,核函数值的衰减速度越慢,表示更宽泛的相似度范围。
- 反之,σ 越小,核函数值的衰减速度越快,表示更狭窄的相似度范围。
核方法在SVM中的应用
在SVM中,使用核方法的目标是最大化间隔,同时最小化误分类。优化问题可以表示为:
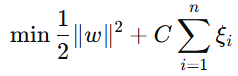
目标函数的两个部分
-
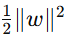 :这个部分是我们原来的目标,用来最大化间隔。这部分确保了我们的分类器具有良好的泛化能力。在支持向量机中,我们希望找到一个能最大化两个类别之间间隔的超平面。间隔定义为超平面到最近数据点的距离。在数学上,间隔可以表示为
:这个部分是我们原来的目标,用来最大化间隔。这部分确保了我们的分类器具有良好的泛化能力。在支持向量机中,我们希望找到一个能最大化两个类别之间间隔的超平面。间隔定义为超平面到最近数据点的距离。在数学上,间隔可以表示为 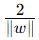 。通过最小化
。通过最小化 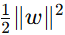 ,我们实际上是在最大化间隔
,我们实际上是在最大化间隔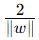 。因为
。因为 越小,间隔越大。这样可以使分类器具有更好的泛化能力。
上述方程即给出了SVM最优化问题的约束条件。
支持向量上的样本点:
-
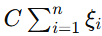 :这部分是惩罚项,用来控制松弛变量的总和。松弛变量
:这部分是惩罚项,用来控制松弛变量的总和。松弛变量 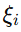 表示第 i 个样本违反间隔的程度。C 是一个正则化参数,用来平衡间隔最大化和误分类样本之间的关系。
表示第 i 个样本违反间隔的程度。C 是一个正则化参数,用来平衡间隔最大化和误分类样本之间的关系。- 如果 C 很大,模型会更加关注减少误分类,但可能会过拟合训练数据。
- 如果 C 很小,模型会更关注最大化间隔,但可能会欠拟合。
其中,约束条件是:
![]()
引入对偶问题
为了解决这个优化问题,我们引入拉格朗日乘子![]() 并构建拉格朗日函数:
并构建拉格朗日函数: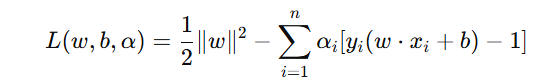
对 w 和 b 求偏导数并令其为零:
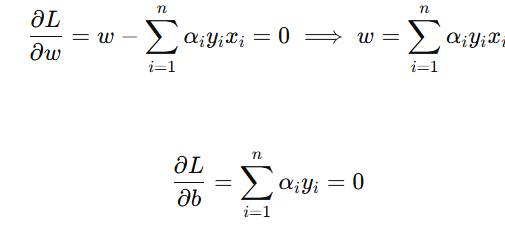
得到对偶问题: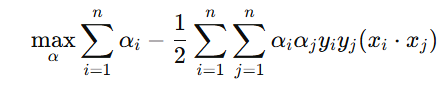
约束条件: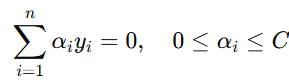
对于非线性可分的数据,我们引入核函数 K(xi,xj)来计算高维空间中的内积,对偶问题变为:
通过序列最小优化(SMO)算法能得到α,再根据α,我们就可以求解出w和b,进而求得我们最初的目的:找到超平面,即"决策平面"。首先,权重向量 w 可以表示为
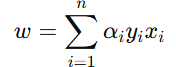
偏置 b 可以通过支持向量求得。对于任何一个支持向量 xk: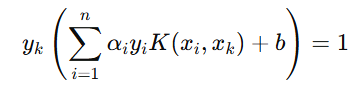
我们可以通过求解这个方程来得到 b。通常通过取所有支持向量的平均值来计算 b: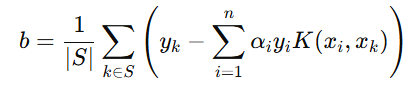 其中 S 是支持向量的集合
其中 S 是支持向量的集合
由于 w 可以用支持向量表示,决策函数可以写成:
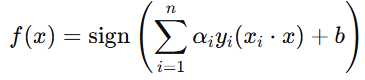
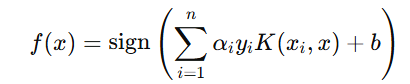
更详细推导参考:机器学习实战教程(八):支持向量机原理篇之手撕线性SVM (cuijiahua.com)
为什么要将求解SVM的原始问题转换为其对偶问题?
- 对偶问题往往更易求解(当我们寻找约束存在时的最优点的时候,约束的存在虽然减小了需要搜寻的范围,但是却使问题变得更加复杂。为了使问题变得易于处理,我们的方法是把目标函数和约束全部融入一个新的函数,即拉格朗日函数,再通过这个函数来寻找最优点。)
- 自然引入核函数,进而推广到非线性分类问题
为什么SVM要引入核函数?
当样本在原始空间线性不可分时,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分
SVM中硬间隔和软间隔
硬间隔分类即线性可分支持向量机,软间隔分类即线性不可分支持向量机,利用软间隔分类时是因为存在一些训练集样本不满足函数间隔(泛函间隔)大于等于1的条件,于是加入一个非负的参数 ζ (松弛变量),让得出的函数间隔加上 ζ 满足条件。
SVM如何处理多分类问题?
支持向量机(SVM)最初是为二分类问题设计的,但它也可以扩展到多分类问题。主要有两种常见的方法来处理多分类问题:一对一(one-vs-one)和一对多(one-vs-rest)。
一对一(One-vs-One)
在一对一方法中,对于一个有 K 个类别的问题,构建 K(K−1)/2个分类器,每个分类器用于区分两个类别。每个分类器都只在两个类别的数据上进行训练。
步骤:
- 训练分类器:对每一对类别 (i,j) 训练一个 SVM 分类器
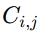 。
。 - 分类:对于一个新的输入样本,让每个分类器进行预测,并记录投票。
- 投票:统计每个类别获得的投票数,选择投票最多的类别作为最终分类结果。
优点:
- 每个分类器只需要处理两类数据,因此相对简单。
- 训练时间和内存消耗相对较低。
缺点:
- 需要训练大量的分类器。
- 需要对每个分类器的输出进行投票统计,预测时间可能较长。
一对多(One-vs-Rest)
在一对多方法中,对于一个有 K 个类别的问题,构建 K 个分类器,每个分类器用于区分一个类别和其他所有类别。
步骤:
- 训练分类器:对每个类别 iii,训练一个 SVM 分类器 Ci,将该类别的数据作为正类,其他类别的数据作为负类。
- 分类:对于一个新的输入样本,让每个分类器进行预测,并得到每个分类器的得分。
- 选择最大得分:选择得分最高的分类器对应的类别作为最终分类结果。
优点:
- 只需要训练 K 个分类器,相对简单。
- 每个分类器处理的数据量较大,模型可能更稳定。
缺点:
- 当类别不平衡时,可能会影响分类器的性能。
- 每个分类器需要处理多类数据,训练时间和内存消耗较大。
高斯径向基核函数(Gaussian Radial Basis Function, RBF)
定义
高斯RBF核函数的数学形式为:
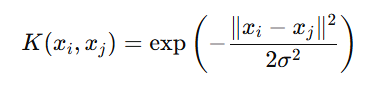
其中:
- xi 和 xj是输入样本的特征向量。
- ∥xi−xj∥ 表示 xi 和 xj 之间的欧氏距离。
- σ 是一个参数,称为带宽参数,控制核函数的“宽度”。
性质
-
非线性映射: RBF核函数通过非线性方式将输入样本映射到高维空间,在这个高维空间中,原本非线性可分的数据可能变得线性可分。
-
局部性: RBF核函数的值取决于输入样本之间的距离。当两个样本距离较近时,RBF核函数值接近1;当两个样本距离较远时,RBF核函数值接近0。这种特性使得RBF核函数对局部模式更加敏感。
-
参数选择: 参数 σ 的选择非常重要。如果 σ 值过大,核函数会变得过于平滑,无法捕捉数据的细节结构;如果 σ 值过小,核函数会变得过于敏感,可能导致过拟合。
应用
高斯RBF核函数广泛应用于SVM分类器中,特别是在以下场景中:
-
非线性分类: RBF核函数可以处理复杂的非线性分类问题,通过将数据映射到高维空间,使得线性分类器在高维空间中能够有效工作。
-
缺少领域知识: 当对数据的分布和模式缺乏先验知识时,RBF核函数是一种默认且可靠的选择,因为它具有良好的适应性。
支持向量中的向量是指什么?
支持向量是指在支持向量机(SVM)算法中,靠近分类决策边界的数据点。这些点决定了决策边界的位置和方向。通过这些支持向量,SVM能够找到最优的分隔超平面,从而最大化两个类之间的间隔。这些点对分类结果有很大的影响,其他的点不会影响决策边界的选择。
LR 与 SVM的区别
损失函数(loss function)不同
lr的损失函数是 cross entropy loss, adaboost的损失函数是 expotional loss ,svm是hinge loss,常见的回归模型通常用 均方误差 loss。
Hinge Loss 的定义
对于一个训练样本 ,其中
是输入特征向量,
是标签(通常是 +1 或 -1),hinge loss 定义如下:
其中是模型的预测结果,通常为:
Hinge Loss 的含义
• 当预测正确且有足够的安全边界时(即 ( )),hinge loss 为 0。这意味着模型对该样本的分类是正确且信心足够高。
• 当预测不正确或没有足够的安全边界时(即 ( )),hinge loss 会随着预测错误的程度而增加。这种情况下,hinge loss 会产生一个正值,表示模型需要调整以更好地分类这个样本。
数学表达和优化问题
在 SVM 的优化问题中,我们希望最小化以下目标函数:
• 是正则化项,用于避免过拟合。
• C 是一个超参数,用于平衡正则化项和 hinge loss 之和。
为什么使用 Hinge Loss
1. 最大化间隔:Hinge loss 鼓励模型不仅正确分类样本,还要使得样本离决策边界尽可能远,从而实现最大化间隔。
2. 稀疏性:Hinge loss 使得只有靠近决策边界的支持向量对模型的参数更新有影响,这种特性有助于提高模型的效率和泛化能力。
支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用)
影响SVM决策面的样本点只有少数的结构支持向量,当在支持向量外添加或减少任何样本点对分类决策面没有任何影响;而在LR中,每个样本点都会影响决策面的结果。
线性SVM不直接依赖于数据分布,分类平面不受一类点影响;LR则受所有数据点的影响,如果数据不同类别strongly unbalance,一般需要先对数据做balancing
在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
这个问题理解起来非常简单。分类模型的结果就是计算决策面,模型训练的过程就是决策面的计算过程。通过上面的第二点不同点可以了解,在计算决策面时,SVM算法里只有少数几个代表支持向量的样本参与了计算,也就是只有少数几个样本需要参与核计算(即kernal machine解的系数是稀疏的)。然而,LR算法里,每个样本点都必须参与决策面的计算过程,也就是说,假设我们在LR里也运用核函数的原理,那么每个样本点都必须参与核计算,这带来的计算复杂度是相当高的。所以,在具体应用时,LR很少运用核函数机制。
线性SVM依赖数据表达的距离测度,所以需要对数据先做normalization,LR不受其影响
1. 距离测度的依赖:线性 SVM 通过找到最大化两类样本之间间隔的超平面来进行分类。这个过程依赖于样本点之间的距离测度(例如欧氏距离)。
2. 归一化的重要性:如果不同特征的量纲差异很大(例如一个特征的值在 1 到 10 之间,另一个特征的值在 1000 到 10000 之间),这种差异会导致某些特征在计算距离时对结果的影响过大,从而影响 SVM 的性能。归一化可以将所有特征缩放到相同的范围,常见的方法有 min-max 归一化和 z-score 归一化。
3. 归一化方法:
• Min-Max 归一化:将数据缩放到 [0, 1] 的范围:
• Z-score 归一化:将数据转化为均值为 0,标准差为 1 的标准正态分布:
逻辑回归和数据尺度
1. 线性模型的特点:逻辑回归也是一种线性模型,它的目标是通过拟合一个逻辑函数(Sigmoid 函数)来预测二分类的概率。
2. 梯度下降的影响:逻辑回归的损失函数通过梯度下降优化。在梯度下降中,虽然特征的尺度会影响收敛速度,但不会影响模型的最终系数的比值关系。因此,逻辑回归对特征的尺度不太敏感。
3. 标准化的优势:虽然逻辑回归在理论上对不同特征的尺度不敏感,但在实际应用中,对特征进行标准化可以加快梯度下降的收敛速度,并提高模型的稳定性和性能。
特征尺度对梯度下降的影响
1. 梯度下降的基本原理
梯度下降是一种优化算法,用于最小化目标函数。更新规则通常为:
其中:
• \theta 是模型参数。
• \alpha 是学习率。
•是目标函数
关于 \theta 的梯度。
2. 特征尺度对梯度的影响
• 梯度的计算:梯度下降算法计算每个特征的梯度。如果特征的尺度差异很大,那么特征对应的梯度值也会有较大差异。
• 步长不均衡:由于学习率 \alpha 是相同的,如果特征的尺度不同,那么每一步更新的步长会受到特征尺度的影响。较大尺度的特征会导致较大的梯度,更新步长过大,可能导致跳过最优解;较小尺度的特征会导致较小的梯度,更新步长过小,收敛速度慢。3. 特征尺度对收敛速度的具体影响
• 不均衡收敛:不同尺度的特征会导致参数更新速度不均衡,使得某些参数更新过快,另一些更新过慢,整体收敛过程变得不稳定。
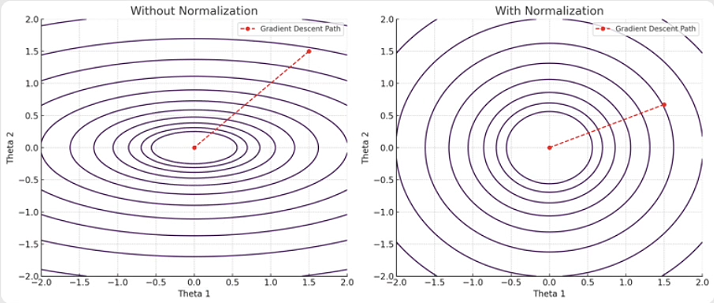
• 等高线图的形状:如果特征尺度不均衡,目标函数的等高线图会变成椭圆形,长轴和短轴的比例差异很大。梯度下降路径会像“之”字形,在长轴方向反复振荡,收敛速度慢。而如果特征经过归一化处理,等高线图会更接近圆形,梯度下降路径更直,收敛速度更快。
这里是两个图示,它们展示了特征尺度如何影响梯度下降的收敛路径:
未归一化时(左图):
- 等高线图呈椭圆形,长轴和短轴的比例差异很大。
- 梯度下降路径像“之”字形,在长轴方向反复振荡,收敛速度慢。归一化后(右图):
- 等高线图更接近圆形。
- 梯度下降路径更直,更快地收敛到最优解。这些图示直观地展示了特征归一化的重要性,可以显著加快梯度下降的收敛速度
4. 归一化和标准化的优势
• 归一化:将特征缩放到相同的范围(如 [0, 1] 或 [-1, 1]),可以使各个特征对梯度的贡献相同,更新步长均衡,加速收敛。
适用情况:
• 特征范围差异大:如果特征的取值范围差异较大,归一化可以将它们缩放到相同范围,使其对模型的贡献均衡。
• 距离度量敏感的算法:如 K-近邻(KNN)、支持向量机(SVM)和神经网络等,这些算法依赖于特征之间的距离,因此需要对特征进行归一化处理• 标准化:将特征转化为均值为 0,标准差为 1 的标准正态分布,可以减少特征之间的尺度差异,同样有助于加快收敛。
适用情况:
• 特征服从正态分布:如果特征大致服从正态分布,标准化可以更好地处理这些特征。
• 线性模型和逻辑回归:如线性回归、逻辑回归和线性判别分析(LDA),这些算法对特征的尺度不敏感,但标准化可以提高其收敛速度和稳定性。
SVM的损失函数就自带正则
这就是为什么SVM是结构风险最小化算法的原因,意思就是在训练误差和模型复杂度之间寻求平衡,防止过拟合,从而达到真实误差的最小化。达到结构风险最小化的目的,最常用的方法就是添加正则项
如何理解结构化风险最小
1. 经验风险与结构化风险
• 经验风险(Empirical Risk):是模型在训练集上的错误率或损失。在机器学习中,通常希望最小化经验风险,但单纯追求经验风险最小化可能导致过拟合,即模型在训练集上表现很好,但在测试集上表现较差。
• 结构化风险(Structural Risk):在经验风险的基础上,加入了对模型复杂度的惩罚项。目标是同时最小化经验风险和模型复杂度,从而提高模型的泛化能力。
2. SVM 的结构化风险最小化
SVM 通过优化一个目标函数来实现结构化风险最小化:
其中:
• 是模型复杂度的度量,用于控制模型的复杂度,防止过拟合。
• C 是一个超参数,用于平衡经验风险和模型复杂度。
• 是经验风险的度量,即 hinge loss。
3. 正则化项的作用
• 正则化项:是模型复杂度的度量,用于控制超平面的复杂度,使其尽可能简单、平滑。通过控制正则化项的大小,可以避免模型过于复杂而导致的过拟合问题。
• 超参数 (C):控制经验风险和结构化风险之间的权衡。较大的 (C) 值会使模型更关注经验风险,可能导致过拟合;较小的 (C) 值会使模型更关注模型复杂度,可能导致欠拟合。通过选择合适的 (C) 值,可以找到经验风险和模型复杂度之间的最佳平衡。
4. 凸优化问题
SVM 的目标函数是一个凸优化问题,具有唯一的全局最优解。这个优化问题的求解保证了在训练集上风险最小化的同时,控制模型复杂度,从而实现结构化风险最小化。
5. 泛化能力
通过结构化风险最小化,SVM 在训练过程中不仅关注训练集的表现,还通过正则化项控制模型的复杂度。这使得 SVM 能够更好地泛化到未见过的测试数据上,提高模型的泛化能力。
L1L2正则化
深入理解L1、L2正则化 - ZingpLiu - 博客园 (cnblogs.com)
L1 正则化(Lasso)
L1 正则化通过添加权重绝对值的总和来惩罚模型的复杂性。其损失函数为: 其中:
- L 是总损失。
- L0 是原始损失(如均方误差)。
- λ 是正则化参数,控制正则化强度。
- wi 是模型的权重。
适用情况
-
特征选择:
- L1 正则化会产生稀疏模型,即许多权重会被驱动到零。这使得 L1 正则化非常适合用于特征选择或处理高维数据。
- 如果你怀疑只有少数特征对模型有显著贡献,可以使用 L1 正则化。
-
高维数据:
- 当数据集有很多特征时,L1 正则化可以帮助减少模型复杂性,挑选出重要特征。
稀疏性的原因
L1 正则化会导致某些权重 wi 被驱动到零,这是因为 L1 正则化的优化过程倾向于产生稀疏解。以下是其具体原因:
-
绝对值函数的形状:
- 绝对值函数 ∣w∣ 在 w=0 处具有尖锐的拐点。这使得优化过程更容易将权重推向零。
- 相比之下,L2 正则化的平方函数在 w=0 处是平滑的,不容易将权重推向零。
-
优化过程:
- 在优化过程中,L1 正则化倾向于选择一些特征的权重为零,而不是让所有特征的权重都变得很小。这是因为 L1 正则化在权重为零处具有更强的吸引力。
-
几何解释:
- 在几何上,L1 正则化对应的等高线是菱形,而 L2 正则化对应的等高线是圆形。
- 当与损失函数的等高线相交时,L1 正则化的菱形等高线更可能在坐标轴上与损失函数的等高线相切,从而导致某些权重为零。
L1 正则化如何实现特征选择
-
绝对值惩罚:
- L1 正则化通过在损失函数中添加权重绝对值的总和来惩罚模型的复杂性。
- 这个绝对值惩罚使得在优化过程中,许多不重要的特征的权重被驱动到零。
-
稀疏解:
- L1 正则化的稀疏性意味着优化过程更倾向于选择一些特征的权重为零。
- 这意味着模型只保留了那些对预测任务最重要的特征,从而实现特征选择
L2 正则化(Ridge)
L2 正则化通过添加权重平方的总和来惩罚模型的复杂性。其损失函数为:
- 通过惩罚大权重,防止过拟合。
- 不会产生稀疏模型(权重不会被驱动到零)
适用情况
-
防止权重过大:
- L2 正则化会惩罚大权重,鼓励模型使用所有特征的较小权重。这有助于防止模型过拟合。
- 如果你认为所有特征都对预测有贡献,但不希望其中某些特征的权重过大,可以使用 L2 正则化。
-
数值稳定性:
- L2 正则化可以提高模型的数值稳定性,特别是在多重共线性(特征之间高度相关)的情况下。
多重共线性
定义
多重共线性是指在回归模型中,多个特征变量之间存在高度相关性,这会导致模型估计的不稳定性。例如,如果有两个特征 x1 和 x2 彼此高度相关,那么它们在解释目标变量 y 时提供的信息会有很大的重叠。
问题
多重共线性会导致以下问题:
- 回归系数的不稳定性:因为高度相关的特征彼此竞争解释目标变量的方差,导致回归系数的估计值对训练数据的微小变化非常敏感。
- 解释困难:很难判断每个特征对目标变量的独立贡献。
- 数值问题:当特征矩阵 X 的列高度相关时,矩阵
的行列式接近零,导致其不可逆或接近奇异,影响回归模型的计算。
L2 正则化能够减轻多重共线性带来的问题,主要通过以下方式:
- 惩罚大权重:
- L2 正则化通过惩罚权重的平方,防止某些特征的权重过大。这样,可以平滑地分配权重,使得模型不依赖于某些特定的特征。
- 增加矩阵
的对角元素:
- 在加入正则化项后,回归问题的矩阵求解变为
,其中 III 是单位矩阵。
- 这相当于对
的对角线元素增加了 λ,使得矩阵变得更稳定和可逆,从而减轻了多重共线性的问题。
数值稳定性
定义
数值稳定性指的是算法在面对数据中的微小变化时能否保持稳定的输出。这在处理浮点数计算时尤为重要,因为浮点数计算可能会引入舍入误差。
L2 正则化的贡献
通过惩罚大权重,L2 正则化能减少模型对训练数据中噪声的敏感性,从而提高模型的数值稳定性。具体表现在以下几个方面:
减少模型复杂性:
- 大权重通常意味着模型在努力拟合训练数据中的噪声。通过惩罚大权重,L2 正则化可以简化模型,使其更加平滑和稳定。
提高泛化能力:
- 正则化减少了模型对训练数据的过拟合,从而提高了模型在新数据上的表现,即提高了模型的泛化能力。
组合使用(Elastic Net)
机器学习算法系列(六)- 弹性网络回归算法(Elastic Net Regression Algorithm)_elasticnet回归-CSDN博客
在某些情况下,结合 L1 和 L2 正则化的 Elastic Net 方法可能是更好的选择。Elastic Net 正则化的损失函数为:
其中:
- λ1 控制 L1 正则化的强度。
- λ2 控制 L2 正则化的强度。
适用情况
- 特征选择和稳定性:
- Elastic Net 可以同时进行特征选择和保持模型稳定性。
- 当特征数量大于样本数量,或特征之间存在高度相关性时,Elastic Net 会表现得更好。
超参选择
交叉验证的步骤
划分数据集:
- 将数据集划分为 kkk 个不重叠的子集,称为折(folds)。常见的选择是 k=5 或 k=10。
训练和验证:
- 对每个超参数值,进行 k-折交叉验证。在每一次交叉验证中,选择其中一个子集作为验证集,其余的子集作为训练集。
- 在训练集上训练模型,并在验证集上评估模型的性能。记录每个折的验证误差。
计算平均验证误差:
- 对于每个超参数值,计算 k 次验证误差的平均值,作为该超参数值的最终验证误差。
选择最佳超参数:
- 选择验证误差最小的超参数值作为模型的最终超参数。
4、LDA 线性判别分析算法(Linear Discriminant Analysis Algorithm)
参考文章:
机器学习算法系列(十)-线性判别分析算法(一)(Linear Discriminant Analysis Algorithm)_线性判别算法-CSDN博客
线性判别分析LDA原理总结 - 刘建平Pinard - 博客园 (cnblogs.com)
线性判别分析(Linear Discriminant Analysis, LDA)不仅是分类工具,也是一种常用的降维技术。它通过找到能够最大化类间分散性与类内分散性比值的投影方向,将高维数据映射到低维空间,从而达到降维的目的。以下是详细的推导过程和步骤:
LDA 降维的目标
LDA 的目标是找到一个投影矩阵 W,将原始高维数据 X 投影到低维空间 X′,使得投影后的数据在低维空间中具有最大的类间散布和最小的类内散布。
基本步骤
-
计算类别均值和总均值:
- 计算每个类别的均值向量
。
- 计算所有样本的总均值向量
。
- 计算每个类别的均值向量
-
计算类内散布矩阵
:
- 类内散布矩阵衡量同一类别的样本之间的散布程度。
- 对于每个类别 i,计算其类内散布矩阵:

- 总的类内散布矩阵为:
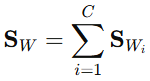
-
计算类间散布矩阵
:
- 类间散布矩阵衡量不同类别均值之间的散布程度。
- 类间散布矩阵为:

- 其中 ni 是类别 i 的样本数量。
-
求解广义特征值问题:
- LDA 的目标是最大化投影后的类间散布和类内散布的比值:

- 这个问题可以转化为广义特征值问题:
 这个特征值问题表示 w是矩阵
这个特征值问题表示 w是矩阵 的特征向量,λ 是其特征值
- 求解这个特征值问题,找到前 k 个最大的特征值对应的特征向量,组成投影矩阵 W。
- LDA 的目标是最大化投影后的类间散布和类内散布的比值:
-
数据投影:
- 使用投影矩阵 W 将原始数据 X 投影到低维空间:
- 使用投影矩阵 W 将原始数据 X 投影到低维空间:
LDA最多能降到C − 1的维数
类间散布矩阵  的秩
的秩
类间散布矩阵 定义为:
![]()
其中:
- C 是类别的数量。
由于 是由 C 个类别均值的差构成的矩阵的外积求和得到的,且这些均值差向量都在 C−1 维的子空间内,因此
的秩最多为 C−1。
投影的维数
LDA 的投影方向是通过最大化类间方差和最小化类内方差的比值来确定的。这可以通过求解广义特征值问题得到
这里的特征向量 w 对应于投影方向,特征值 λ 表示在这些方向上的投影方差。
由于 的秩最多为 C−1,所以这个广义特征值问题最多有 C−1 个非零特征值。因此,最多可以找到 C−1 个特征向量,也就是可以将数据投影到最多 C−1 维的子空间。
直观理解
直观上可以理解为,如果有 C 个类别,我们需要 C−1 维度来区分开所有的类别。例如:
- 对于两个类别(C=2),我们需要一个维度(C−1=1)来区分它们。
- 对于三个类别(C=3),我们需要两个维度(C−1=2)来区分它们,以此类推。
概率分布角度:
机器学习算法系列(十一)-线性判别分析算法(二)(Linear Discriminant Analysis Algorithm)_机器学习 判别算法-CSDN博客
机器学习算法系列(十二)-二次判别分析算法(Quadratic Discriminant Analysis Algorithm)-CSDN博客
5、朴素贝叶斯分类
机器学习算法系列(十三)-朴素贝叶斯分类算法(Naive Bayes Classifier Algorithm)_朴素贝叶斯的前提-CSDN博客
朴素贝叶斯分类器的基本原理
朴素贝叶斯分类器基于以下两个假设:
- 特征独立性假设:假设所有特征是独立的,给定类别 C 下,每个特征 xi 的概率是独立的。
- 贝叶斯定理:用于计算后验概率。
贝叶斯定理
贝叶斯定理用于计算后验概率 P(C∣X):
![]()
其中:
- P(C∣X) 是给定特征向量 X 时类别 C 的后验概率。
- P(X∣C) 是在类别 C 下观察到特征向量 X 的似然。
- P(C) 是类别 C 的先验概率。
- P(X) 是观察到特征向量 X 的边际概率。
朴素贝叶斯的简化
由于特征独立性假设,似然 P(X∣C) 可以表示为所有特征条件概率的乘积:
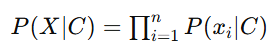
因此,贝叶斯定理可以写为:
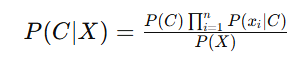
由于 P(X) 对所有类别 C 都是相同的,可以忽略这个项,只需比较分子部分的大小即可:
![]()
分类决策
给定一个新的特征向量 X,朴素贝叶斯分类器选择具有最高后验概率的类别 C:
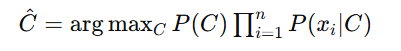
常见的朴素贝叶斯分类器
1. 高斯朴素贝叶斯(Gaussian Naive Bayes)
适用于连续特征,假设特征值服从正态分布。
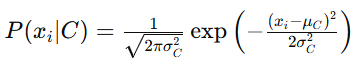
2. 多项式朴素贝叶斯(Multinomial Naive Bayes)
适用于离散特征,通常用于文本分类。
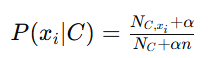
其中:
是类别 C 中特征 xi 的计数。
是类别 C 中所有特征的总计数。
- α 是平滑参数(通常使用拉普拉斯平滑)。
3. 伯努利朴素贝叶斯(Bernoulli Naive Bayes)
适用于二元离散特征。
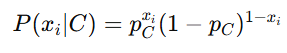
- 先验概率 P(C)P(C)P(C):在没有观察到数据之前对类别 CCC 的初始估计。
- 后验概率 P(C∣X)P(C|X)P(C∣X):在观察到数据 XXX 之后对类别 CCC 的修正概率。
- 似然 P(X∣C)P(X|C)P(X∣C):在给定类别 CCC 的情况下观察到数据 XXX 的概率。
6、 决策树
基于信息熵
信息熵的直观理解
信息熵可以理解为系统中不确定性的度量。假设有一个系统,这个系统可能处于多种状态,每种状态出现的概率不同。信息熵量化了这些状态的不确定性。
- 高熵:如果系统的状态分布均匀(即每种状态的出现概率相同),则系统的不确定性最大,信息熵较高。
- 低熵:如果系统的状态分布非常偏向某种状态(即某些状态的出现概率很高,其他状态的出现概率很低),则系统的不确定性较低,信息熵较低。
1. 计算数据集的初始信息熵 H(D)
对于数据集 D,其信息熵 H(D) 定义为:
![]()
其中:
- k 是类别的数量。
- P(ci) 是数据集中属于类别 ci 的样本的概率。
2. 计算特征的条件信息熵 H(D∣A)
对于特征 A,其条件信息熵 H(D∣A) 定义为:
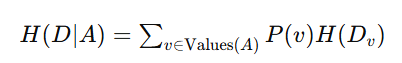
其中:
- Values(A) 是特征 A 的所有可能取值。
- P(v) 是数据集中特征 A 取值为 v 的样本的比例。
是在特征 A 取值为 v 的情况下数据集的熵。
3. 计算信息增益
信息增益定义为:
![]()
4. 选择信息增益最大的特征进行分割:
- 选择信息增益最大的特征作为当前节点的分割特征。
示例
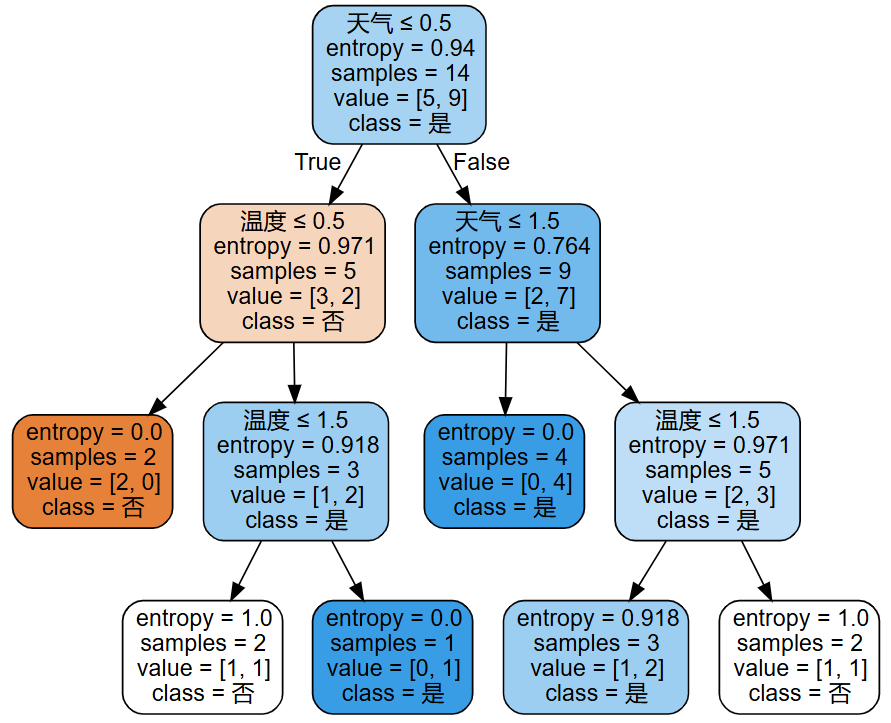
基于基尼指数
基尼值(Gini Value)
基尼值用于衡量一个数据集中样本分类的纯度,定义如下:
![]()
其中:
- Gini(D)是数据集 D 的基尼值。
- P(ci)是数据集中属于类别 ci 的样本的概率。
- k 是类别的数量。
基尼值越小,数据集的纯度越高。
基尼指数(Gini Index)
基尼指数用于衡量一个特征在划分数据集时所带来的纯度变化,定义如下:
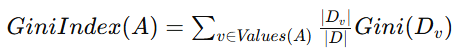
其中:
是特征 A 的基尼指数。
- Values(A) 是特征 A 的所有可能取值。
是特征 A 取值为 v 的数据子集。
是子集
的样本数量。
- ∣D∣ 是数据集 D 的样本数量。
基尼指数越小,表示特征 A 分割数据集后纯度越高。
选择基尼指数最小的特征作为当前节点的分割特征

回归树
基本概念
-
分割标准:
- 决策树回归使用均方误差(Mean Squared Error, MSE)作为分割标准。每次分割后,选择使得子集均方误差最小的特征和分割点。

- 决策树回归使用均方误差(Mean Squared Error, MSE)作为分割标准。每次分割后,选择使得子集均方误差最小的特征和分割点。
-
叶节点预测:
- 在每个叶节点上,决策树使用该节点中所有样本目标值的平均值作为预测值。
-
树的构建:
- 递归地选择最佳分割点,将数据集分割成更小的子集,直到满足停止条件(如叶节点中的样本数小于某个阈值,或均方误差小于某个阈值)。
决策树回归的优点和缺点
优点
- 简单易理解:决策树结构直观,易于解释。
- 非线性关系:能够捕捉数据中的非线性关系。
- 少量数据准备:不需要像其他模型那样对数据进行大量的预处理。
- 处理缺失值:可以处理缺失值,不需要进行插补。
缺点
- 过拟合:决策树容易过拟合,特别是当树的深度较大时。
- 不稳定:对数据的微小变化敏感,可能导致树结构的显著变化。
- 偏差:可能存在高偏差,尤其是在树深度较小时。
示例:预测房价
假设我们有一个小型数据集,用于预测房价。数据集中有以下特征:
面积(平方英尺)房间数
目标是根据 面积 和 房间数 来预测 房价。
数据集
| 样本 | 面积 (平方英尺) | 房间数 | 房价 (千美元) |
|---|---|---|---|
| 1 | 1500 | 3 | 300 |
| 2 | 1700 | 3 | 350 |
| 3 | 1600 | 2 | 280 |
| 4 | 1400 | 2 | 250 |
| 5 | 1800 | 4 | 400 |
| 6 | 1900 | 4 | 450 |
步骤 1:选择最优分割
选择分割特征和分割点
假设我们尝试用 面积 进行第一次分割。我们计算多个分割点的均方误差(MSE),例如分割点为 1600 和 1700。
-
分割点 1600:
- 分割成两个子集:面积 ≤ 1600 和 面积 > 1600。
子集1(面积 ≤ 1600):
- 样本1, 样本3, 样本4
子集2(面积 > 1600):
- 样本2, 样本5, 样本6
-
分割点 1700:
- 分割成两个子集:面积 ≤ 1700 和 面积 > 1700。
子集1(面积 ≤ 1700):
- 样本1, 样本2, 样本3, 样本4
子集2(面积 > 1700):
- 样本5, 样本6
步骤 2:计算均方误差(MSE)
对于每个分割点,计算子集的均方误差:
-
分割点 1600:
-
子集1的平均房价 = (300 + 280 + 250) / 3 = 276.67
-
子集2的平均房价 = (350 + 400 + 450) / 3 = 400.00
-
子集1的MSE = [(300-276.67)^2 + (280-276.67)^2 + (250-276.67)^2] / 3 = 588.89
-
子集2的MSE = [(350-400)^2 + (400-400)^2 + (450-400)^2] / 3 = 1666.67
-
总MSE = (3/6) * 588.89 + (3/6) * 1666.67 = 1127.78
-
-
分割点 1700:
-
子集1的平均房价 = (300 + 350 + 280 + 250) / 4 = 295.00
-
子集2的平均房价 = (400 + 450) / 2 = 425.00
-
子集1的MSE = [(300-295)^2 + (350-295)^2 + (280-295)^2 + (250-295)^2] / 4 = 962.50
-
子集2的MSE = [(400-425)^2 + (450-425)^2] / 2 = 625.00
-
总MSE = (4/6) * 962.50 + (2/6) * 625.00 = 862.50
-
步骤 3:选择最优分割点
通过比较分割点的总MSE,我们选择最优分割点:
- 分割点 1600 的总MSE = 1127.78
- 分割点 1700 的总MSE = 862.50
由于分割点 1700 的总MSE更小,我们选择 1700 作为第一次分割点。
步骤 4:递归构建子树
重复上述步骤,递归地为每个子集选择最优分割点,直到满足停止条件(例如,子集中的样本数少于某个阈值)。

剪枝
预剪枝(Pre-pruning)
预剪枝是在树构建过程中,通过设置停止条件来限制树的生长。这些条件包括:
max_depth:限制树的最大深度。min_samples_split:节点必须包含的最小样本数目,以便进行进一步的分割。min_samples_leaf:叶节点中必须包含的最小样本数目。max_leaf_nodes:限制叶节点的最大数量。min_impurity_decrease:分裂节点时要求的不纯度减少量。
后剪枝(Post-pruning)
后剪枝是在树完全构建后,通过剪掉不必要的子树来简化树结构。常见的后剪枝方法有:
- 成本复杂度剪枝(Cost Complexity Pruning):又称为剪枝回归树(Pruned Regression Tree),通过计算每个节点的误差及其剪枝后的误差,比较其剪枝前后的效果来决定是否剪枝。
成本复杂度剪枝
成本复杂度剪枝通过引入一个参数 α来权衡树的复杂度和误差。对于每个子树 T ,定义损失函数为: ![]()
其中:
- R(T) 是树 T 的误差(例如均方误差)。
- ∣T∣ 是树 T 的叶节点数。
- α 是惩罚参数,用于控制树的复杂度。
通过选择不同的 α 值,我们可以找到最佳的树结构。
- 通过引入 α,我们在误差和模型复杂度之间找到一个平衡点。
- α 越大,模型倾向于简单(树越小),减少过拟合的风险。
- α 越小,模型倾向于复杂(树越大),增加捕捉数据细节的能力。
三种常见的决策树算法
ID3 算法
ID3(Iterative Dichotomiser 3) 算法由 Ross Quinlan 开发,是构建决策树的经典算法之一。ID3 使用信息增益作为节点分割的标准。
特点
- 分割标准:信息增益
- 处理数据类型:主要处理离散数据
- 树构建策略:贪婪算法,从根节点开始选择具有最大信息增益的特征进行分割,递归构建子树
信息增益
信息增益衡量在给定特征的条件下,目标变量的不确定性减少的程度。其计算公式为:
![]()
C4.5 算法
C4.5 也是由 Ross Quinlan 开发的,是对 ID3 的改进。C4.5 使用信息增益率来选择节点分割特征。
特点
- 分割标准:信息增益率
- 处理数据类型:处理离散和连续数据
- 树构建策略:基于信息增益率选择最优特征进行分割,处理缺失值和剪枝
信息增益率
信息增益率是信息增益和固有值的比值。其计算公式为:
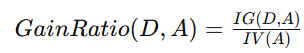
其中:
- IG(D,A) 是特征 A 对数据集 D 的信息增益
- IV(A) 是特征 A 的固有值,计算公式为:
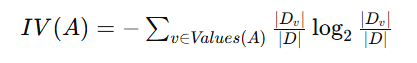
CART 算法
CART(Classification and Regression Trees) 由 Leo Breiman 等人开发,用于分类和回归。CART 使用基尼指数(分类)或均方误差(回归)作为节点分割的标准。
特点
- 分割标准:
- 分类树:基尼指数
- 回归树:均方误差(MSE)
- 处理数据类型:处理离散和连续数据
- 树构建策略:二元分割,每个节点只有两个子节点,使用剪枝来防止过拟合
7.随机森林
Bagging(Bootstrap Aggregating)
Bagging 是一种集成学习技术,主要用于减少模型的方差,提高模型的泛化能力。Bagging 的全称是 Bootstrap Aggregating,它结合了自助采样(Bootstrap sampling)和聚合(Aggregating)的思想。
关键概念
- 自助采样(Bootstrap Sampling):
- 自助采样是一种有放回的抽样方法,从原始数据集中随机抽取若干个样本,生成多个子数据集。每个子数据集的大小与原始数据集相同,但由于是有放回抽样,子数据集中可能包含重复的样本。
- 聚合(Aggregating):
- 聚合是将多个模型的结果进行组合,得到最终的预测结果。对于分类任务,通过投票机制决定最终分类结果;对于回归任务,通过取平均值得到最终预测结果。
随机特征选择的原理
在随机森林中,随机特征选择的步骤如下:
- 数据集准备:从原始数据集中生成多个自助样本(Bootstrap samples),每个样本用于训练一棵决策树。
- 节点分裂:
- 对于每个节点,随机选择一个特征子集,而不是考虑所有特征。
- 在选定的特征子集中,找到最佳分裂点来分割数据。
- 树的生成:递归地在每个节点上重复上述过程,直到满足停止条件(例如,达到最大深度或最小样本数)。
这种方法增加了模型的多样性,因为每棵树不仅在不同的自助样本上训练,而且在每个节点上只考虑特征的随机子集。
投票机制(分类)
对于分类任务,随机森林通过多数投票来决定最终分类结果,即选择出现次数最多的类别。
平均机制(回归)
对于回归任务,随机森林通过对所有树的预测结果取平均值来得到最终的回归值。
包外估计(Out-of-Bag Estimate,简称OOB估计)
是一种用于评估集成学习模型(如随机森林)性能的有效方法。OOB估计基于自助法(Bootstrap Sampling),利用未被抽样的数据(即包外数据)进行模型评估,而不需要额外的验证集。
原理
在随机森林中,每棵决策树都是通过自助法生成的子数据集进行训练的。具体来说,每次从原始数据集中有放回地抽取样本,生成一个与原始数据集大小相同的训练子集。由于是有放回抽样,原始数据集中大约有 36.8% 的样本不会被选中,这些未被选中的样本称为包外数据(Out-of-Bag Data)。
OOB估计的步骤
- 生成自助样本:从原始数据集中有放回地抽取样本,生成多个自助样本,每个样本用于训练一棵决策树。
- 训练模型:在每个自助样本上训练一棵决策树。
- OOB评估:对于每个样本,利用那些未包含该样本的决策树进行预测,汇总这些预测结果计算性能指标(如准确率、均方误差等)。
优点
- 无需额外的验证集:OOB估计利用包外数据进行模型评估,不需要将数据集划分为训练集和验证集,节省了数据。
- 内置评估机制:随机森林的OOB估计提供了一种内置的模型评估机制,可以实时评估模型性能。
- 稳定可靠:OOB估计通常提供与交叉验证相似的结果,具有较好的稳定性和可靠性。
随机森林优缺点
优点
- 高准确性:通过集成多棵树的结果,随机森林通常比单一决策树更准确。
- 抗过拟合:通过Bagging和随机特征选择,随机森林有效地降低了过拟合的风险。
- 处理高维数据:能够处理大量特征数据,并且在特征选择过程中不会丢失重要特征。
- 处理缺失值:具有较好的处理缺失值的能力。
- 计算特征重要性:能够计算每个特征对模型的贡献,便于进行特征选择。
在单棵决策树中,每个节点都用某个特征进行分裂,分裂前后的不纯度变化反映了该特征的重要性。
缺点
- 计算量大:需要训练大量的决策树,计算和内存开销较大。
- 可解释性差:相比单一决策树,随机森林的集成结果较难解释。
- 对含噪声数据敏感:对于含噪声的训练集,随机森林可能会过拟合噪声。
随机森林中的“随机”指
主要指以下两个方面:
- 随机采样数据(Bootstrap Sampling)
- 随机选择特征(Random Feature Selection)
这两个随机过程增加了模型的多样性,减少了过拟合的风险
随机森林填充
(机器学习)随机森林填补缺失值的思路和代码逐行详解-CSDN博客
- 初始填充:首先使用简单的方法(如均值、中位数填充)来填充缺失值,以便进行随机森林的初始训练。
- 随机森林训练:使用随机森林模型对每个具有缺失值的特征进行训练,预测这些特征的缺失值。
- 迭代更新:重复步骤2,使用更新后的预测值重新训练随机森林模型,直到填充值收敛或达到预设的迭代次数。
8. AdaBoost
Adaboost入门教程——最通俗易懂的原理介绍(图文实例)_adaboost算法原理图-CSDN博客
AdaBoost原理详解 - ScorpioLu - 博客园 (cnblogs.com)
具体推导:
机器学习算法系列(十九)-自适应增强算法(Adaptive Boosting Algorithm / AdaBoost Algorithm)——下篇_自适应增强算法用在自动控制中-CSDN博客
AdaBoost(Adaptive Boosting)是一种集成学习算法,旨在提高分类器的准确性。它通过组合多个弱分类器(通常是决策树桩)来形成一个强分类器。
工作原理
AdaBoost通过迭代地训练弱分类器,并在每次迭代中调整样本的权重,以便后续的分类器更关注前一次分类错误的样本。具体步骤如下:
-
初始化权重:对每个训练样本赋予相等的权重。
-
迭代训练:
- 在每一轮迭代中,根据当前权重训练一个弱分类器。
- 计算分类错误率。
- 根据分类错误率计算该分类器的权重(分类器的影响力)。
- 更新样本权重,使得分类错误的样本权重增加,而分类正确的样本权重减少。
-
组合分类器:最终分类器是所有弱分类器的加权和,分类器权重越大,其影响力越大。
公式与步骤
初始化权重
每个样本的初始权重为:![]() 其中,N 是样本总数。
其中,N 是样本总数。
训练弱分类器
在每一轮迭代 t 中:
-
使用权重
训练弱分类器
。
-
计算分类错误率
:
其中,
是指示函数,yi 是实际标签,
是预测标签。
-
计算分类器权重
:
-
更新样本权重:
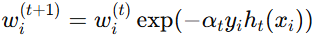 并进行归一化,使得所有样本权重之和为1。
并进行归一化,使得所有样本权重之和为1。
最终分类器
最终分类器 H(x) 是弱分类器的加权和:
![]()
优点
- 高准确性:通过组合多个弱分类器,AdaBoost通常能显著提高分类准确性。
- 无需特征选择:AdaBoost自动关注最有用的特征,适用于高维数据。
- 简单且有效:易于实现,且在各种任务中表现良好。
缺点
- 对噪声敏感:对数据中的噪声和异常值比较敏感,因为这些样本的权重可能会被过度提高。
- 计算复杂度高:每次迭代需要重新训练分类器,计算量较大。
几种不同的 AdaBoost 算法变体
分类算法
-
AdaBoost.M1
- 简介:AdaBoost.M1 是最早的 AdaBoost 算法,由 Freund 和 Schapire 提出。
- 特点:适用于二分类和多分类问题。每一轮的分类器权重由分类错误率决定,错误率不能超过 0.5。
-
AdaBoost.M2
- 简介:AdaBoost.M2 是 AdaBoost.M1 的改进版,能够处理多分类问题。
- 特点:在处理多分类问题时,比 AdaBoost.M1 更有效。通过引入伪损失(pseudo loss)来衡量分类错误,调整分类器权重。
-
AdaBoost-SAMME
- 简介:SAMME(Stagewise Additive Modeling using a Multiclass Exponential loss function)是一种多分类扩展,类似于 AdaBoost.M2。
- 特点:适用于多分类问题,通过引入多分类的指数损失函数来调整分类器权重。
-
AdaBoost-SAMME.R
- 简介:SAMME.R 是 SAMME 的改进版,利用回归模型来处理多分类问题。
- 特点:使用真实值而不是离散类别来进行预测,能够更好地处理多分类问题。
回归算法
-
AdaBoost.R1
- 简介:AdaBoost.R1 是最早的 AdaBoost 回归版本,适用于回归问题。
- 特点:通过调整样本权重来提高回归模型的准确性,目标是最小化平方误差。
-
AdaBoost.R2
- 简介:AdaBoost.R2 是 AdaBoost.R1 的改进版。
- 特点:通过引入绝对误差和相对误差的综合衡量标准,改进了回归模型的性能。
9. 梯度提升决策树算法(Gradient Boosted Decision Trees / GBDT)
参考文章:简单易学的机器学习算法——梯度提升决策树GBDT_决策树 梯度 参数 搜索-CSDN博客
GBDT原理详解 - ScorpioLu - 博客园 (cnblogs.com)
机器学习算法系列(二十)-梯度提升决策树算法(Gradient Boosted Decision Trees / GBDT)-CSDN博客
GBDT 的基本思想
GBDT 通过逐步减小损失函数(例如,均方误差、对数损失等)的梯度来优化模型。在每一轮迭代中,GBDT 训练一棵新的决策树,这棵树拟合前一轮模型的残差(即预测误差)。新的树用来修正前一轮的预测结果,从而使整体模型的误差逐渐减小。
GBDT 的算法步骤
-
初始化模型:初始化模型为常数值,通常是使损失函数最小化的值。

其中,L 是损失函数,yi 是实际值,c 是常数。
-
迭代训练: 对于每一轮
:
-
计算当前模型的残差(负梯度)。
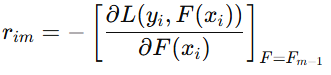
其中,
是第 i 个样本在第 m 轮的残差,
是第 m−1 轮的模型。
-
训练一棵新的决策树,拟合当前的残差。

其中,
是第 m 轮的新决策树。
-
更新模型,加入新的树。
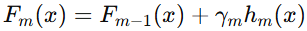
其中,
是学习率,控制每棵树的影响力。
-
-
最终模型:经过 M 轮迭代,最终模型为:
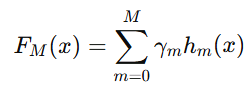
损失函数的数值优化可以看成是在函数空间,而不是在参数空间
参数空间 vs. 函数空间
-
参数空间:传统机器学习算法通常在参数空间中进行优化,即优化模型参数,使损失函数最小化。例如,线性回归中我们优化权重参数 θ\thetaθ。
-
函数空间:在函数空间中进行优化意味着我们在一组函数中进行选择或优化,以最小化损失函数。例如,在提升方法中,我们逐步添加新的基函数,以减小当前模型的损失。
提升方法(Boosting)中的函数空间优化
提升方法,如 AdaBoost 和梯度提升树(Gradient Boosting Trees),就是在函数空间中进行优化的经典示例。
AdaBoost
在 AdaBoost 中,每一步都会训练一个新的弱分类器,目的是提高前一步分类器的错误。
在这个过程中,我们不断地在函数空间中添加新的基分类器,每一个基分类器相当于一个函数。最终的强分类器是这些基分类器的加权和。
梯度提升树(Gradient Boosting Trees)
梯度提升树是另一个在函数空间中进行优化的算法。其基本思想是逐步构建决策树,每棵树都拟合前一棵树的残差。
在这个过程中,每棵新树都相当于一个新的基函数,逐步优化损失函数,形成最终的模型。这个优化过程是通过在函数空间中逐步添加新的基函数来实现的。
数学表述
假设我们有一个初始模型,我们希望通过迭代优化使其逼近目标函数 y。
-
初始模型
:
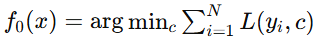
-
在第 m 次迭代中,我们希望找到一个新的基函数
,使得当前模型的残差
得到最小化:
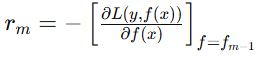
-
新的模型更新为:
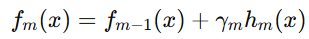 其中
其中 是学习率,决定了新基函数在模型中的权重。
-
继续迭代,直到损失函数收敛。
GBDT中的残差与负梯度
负梯度
负梯度指示了如何调整模型参数以最快地减小损失函数的方向。因此,在每一轮迭代中,我们通过拟合损失函数的负梯度来更新模型:
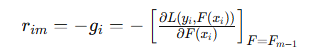
这意味着当前模型的残差实际上是损失函数的负梯度
残差是指模型预测值与真实值之间的差异。在GBDT中,残差是我们希望通过新模型来拟合的目标。
损失函数及其负梯度
让我们具体看看不同损失函数下的负梯度,并理解它们为什么可以视为“残差”。
1. 均方误差(MSE)
均方误差的损失函数为:
![]()
其梯度为: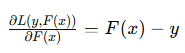
负梯度为: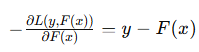
在这里,负梯度直接等于实际值与预测值的差,即残差。
2. 对数损失(Log Loss)
对数损失通常用于二分类问题,其定义为:
![]()
其中,F(x) 是模型输出的概率。其梯度为:
![]()
负梯度为:![]()
在这里,负梯度表示的是一种加权的残差形式,反映了预测值与实际值的差异。
3. 绝对误差损失(Absolute Error Loss)
绝对误差损失函数定义为:
![]()
负梯度为:![]()
在这里,负梯度反映了预测值与实际值的符号差异,即模型需要向哪个方向调整以减小误差。
4. Huber 损失函数
Huber 损失函数在处理异常值时更稳健,其定义为:

负梯度为:
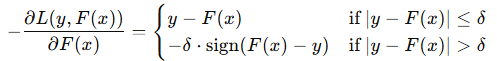
在这里,当误差较小时,负梯度等于残差;当误差较大时,负梯度是一个调整方向的常数,反映了需要减小的调整量。
两种对数损失
逻辑回归中的对数损失函数
逻辑回归用于二分类问题,其损失函数(对数损失)定义为:
其中,
,即逻辑函数(Sigmoid 函数)将线性模型的输出 H(x) 转换为概率。
对于二分类问题,标签 yyy 通常取值为 {0,1},但也可以取 {−1,1}
通过一些变换将其与逻辑回归中的对数损失联系起来
Huber 损失函数
Huber 损失函数是一种对异常值(outliers)具有鲁棒性的损失函数,它在处理回归任务时特别有用。它结合了均方误差(MSE)和绝对误差(MAE)的优点,在误差较小时使用均方误差,在误差较大时使用绝对误差,从而在对小误差进行精细拟合的同时,减少了大误差对模型的影响。
Huber 损失函数的定义
Huber 损失函数定义为:
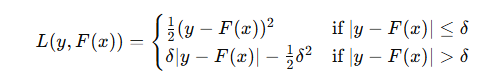
其中,y 是实际值,F(x)是预测值,δ 是一个超参数,用于平衡均方误差和绝对误差。
10. XGBoost
xgboost中的数学原理_xgboost 如何判断分类-CSDN博客
Adaboost、GBDT与XGBoost的区别_adaboost和xgboost的区别-CSDN博客
XGBoost(Extreme Gradient Boosting)是一个基于梯度提升框架的优化分布式机器学习库,专为高效、灵活和可扩展而设计。
主要特点
- 正则化:XGBoost 在损失函数中引入了正则化项,可以有效防止过拟合。
- 支持并行计算:XGBoost 支持并行树构建,大大加快了训练速度。
- 自动处理缺失值:XGBoost 能够自动处理缺失值,无需额外的预处理。
- 支持多种目标函数:XGBoost 支持多种损失函数,包括分类、回归和排序任务。
- 树提升算法优化:XGBoost 在传统的梯度提升树基础上做了多项优化,如支持按节点分裂、缓存意识、分布式计算等。
公式推导
XGBoost 的核心思想与梯度提升树(GBDT)相同,通过逐步添加决策树来优化模型。以下是 XGBoost 的数学推导和公式。
1. 基本模型
假设我们有一个训练集,其中 i=1,2,…,N 模型的预测值为:
![]()
其中, 是第 k 棵决策树,K 是总的决策树数量。
2. 目标函数
XGBoost 的目标函数包括损失函数和正则化项:
![]()
其中,L 是损失函数,Ω 是正则化项。具体地,Ω 可以表示为:
![]()
其中,T 是树的叶节点数, 是叶节点权重,
和 λ 是正则化参数。
3. 二阶泰勒展开
为了优化目标函数,XGBoost 使用二阶泰勒展开来近似损失函数。假设在第 ttt 轮迭代中,我们要添加第 t 棵树 ,则目标函数可以表示为:
![]()
对损失函数 L 进行二阶泰勒展开:
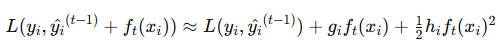
其中,![]() 是一阶导数,
是一阶导数,![]() 是二阶导数。
是二阶导数。
4. 优化目标函数
将二阶泰勒展开代入目标函数:
![]()
对于一棵树,其结构可以表示为:
![]()
其中,q 是将样本映射到叶节点的函数, 是叶节点的权重。
目标函数变为:
![]()
其中,
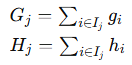
将目标函数对 求导并设为零,得到最优解:
![]()
将 代入目标函数,得到最优目标值:
![]()
分裂叶子节点是怎么决定特征和分裂点的
1. 计算分裂增益
分裂增益衡量的是分裂前后损失的减少量。具体来说,增益可以通过目标函数的减少量来计算。下面是如何计算分裂增益的具体步骤。
增益计算公式
在 XGBoost 中,增益的计算基于二阶泰勒展开的目标函数。对于一个特定的分裂点,增益的公式如下:
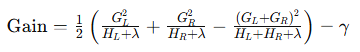
其中:
和
分别是左子节点和右子节点的一阶梯度之和。
和
分别是左子节点和右子节点的二阶梯度之和。
- λ 是正则化参数。
- γ 是叶节点分裂的惩罚项。
- 惩罚小分裂:如果一个分裂带来的增益不足以弥补 γ\gammaγ 的惩罚,那么这个分裂将不会被执行。这样可以避免生成过多的叶节点,使树结构过于复杂。
- 提高分裂标准:只有当分裂带来的增益大于 γ 时,分裂才会被接受。这意味着模型只会进行那些显著提高预测性能的分裂,从而提高模型的泛化能力。
2. 选择最佳分裂点
XGBoost 会遍历所有特征,并对每个特征的所有可能分裂点计算增益。选择增益最大的特征和分裂点进行分裂。
XGBoost 并行加速
1. 并行树构建
在构建决策树时,XGBoost对特征进行分块和并行处理,从而加快分裂点的选择过程。并行树构建的核心思想是对特征和样本进行分块,然后在不同的线程上并行计算增益。
特征分块并行化
XGBoost通过对特征进行分块,并在不同线程上并行计算每个特征的增益,从而加速分裂点的选择过程。
2. 分布式计算
XGBoost支持分布式计算,可以在多台机器上并行训练模型,从而进一步提升训练速度。分布式计算的核心思想是将数据和计算任务分布到多个节点上,并通过通信机制协调各个节点的计算结果。
3. 缓存优化
XGBoost在分裂节点时使用缓存优化技术,通过缓存中间计算结果,减少重复计算,提高效率。
4. 列块结构(Column Block)
XGBoost使用列块结构(Column Block)存储数据,这种结构有助于高效地进行特征分裂和并行计算。
5. 二阶近似(Second-order Approximation)
XGBoost通过二阶泰勒展开进行损失函数的近似,从而更精确地计算增益和更新模型参数。这种方法提高了计算效率和模型的收敛速度。
11. LightGBM
LightGBM(Light Gradient Boosting Machine)是由微软开发的一种高效的梯度提升框架,专为快速训练和低内存占用而设计。它在处理大规模数据集时表现尤为优异,并且在许多机器学习竞赛中被广泛使用。
LightGBM 的主要特点
-
基于直方图的算法:
- LightGBM使用基于直方图的决策树学习算法,将连续特征值离散化为k个离散值,并构建直方图。这样可以显著减少计算量和内存占用。
-
Leaf-wise叶子生长策略:
- 与按层生长的深度优先(level-wise)不同,LightGBM采用按叶子生长的策略(leaf-wise)。这种策略每次选择具有最大增益的叶子进行分裂,从而更快地降低损失。
-
支持类别特征:
- LightGBM可以直接处理类别特征,无需进行独热编码(one-hot encoding),进一步提高了训练速度和模型性能。
-
高效的多线程和分布式训练:
- LightGBM支持多线程和分布式训练,可以在多核CPU和集群环境中高效地训练模型。
-
支持GPU加速:
- LightGBM支持在GPU上进行训练,进一步加速模型的训练过程。
LightGBM 的原理
基于直方图的算法
在LightGBM中,连续特征值被分桶到固定数量的离散值中。这些离散值构建成直方图,每个桶代表一定范围的特征值。这样做有以下优点:
- 减少计算复杂度:在计算分裂增益时,只需要在直方图上进行操作,而不是在原始特征值上。
- 减少内存使用:通过离散化,减少了需要存储的特征值数量。
Leaf-wise叶子生长策略
LightGBM采用叶子生长策略而不是层级生长策略。具体步骤如下:
- 选择叶子:每次选择具有最大分裂增益的叶子节点进行分裂,而不是按层级顺序分裂。
- 更新树结构:更新当前的树结构,记录新的分裂点和叶子节点。
这种策略使得LightGBM在相同复杂度下,能够更快地降低训练误差,但也容易导致树结构不平衡,需要适当的正则化来防止过拟合。
12. k近邻算法(k-Nearest Neighbor / kNN)
kdtree
KD-Tree的原理及其在KNN中的应用(附Python代码)_python kdtree-CSDN博客
KD-Tree 的基本原理
1. 构建KD-Tree
KD-Tree 的构建过程是递归的,主要步骤如下:
- 选择分割维度:选择当前层的分割维度。通常,分割维度是根据当前层数选择的,即如果当前层数为 k,则选择维度 k%d 作为分割维度,其中 d 是数据点的维度数。
- 选择分割点:在当前分割维度上找到中位数点,并将其作为当前节点的分割点。
- 递归构建:根据分割点,将数据点分为左右两部分,递归构建左子树和右子树。
2. KD-Tree 的搜索
KD-Tree 支持多种搜索操作,其中最常用的是最近邻搜索和范围搜索。
最近邻搜索
最近邻搜索的步骤如下:
- 从根节点开始搜索:比较目标点和当前节点的分割点,确定搜索的子树。
- 递归搜索子树:根据比较结果递归搜索左子树或右子树。
- 回溯检查其他子树:在回溯过程中,检查另一个子树是否有可能包含更近的点。如果有可能,则递归检查该子树。
详细的计算步骤:

实例
示例数据
假设我们有以下二维数据点:
![]()
我们希望构建一个 KD-Tree 并找到给定查询点 (9,2) 的最近邻点。
构建 KD-Tree
-
选择分割维度:
- 初始深度为0,选择第0维度(x轴)进行分割。
-
选择分割点:
- 在第0维度上对点进行排序:(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)。
- 选择中位数点作为分割点:中位数点为 (7,2)。
-
递归构建子树:
- 对于左子树,数据点为 (2,3),(4,7),(5,4),当前深度为1,选择第1维度(y轴)进行分割。
- 对于右子树,数据点为 (8,1),(9,6) 当前深度为1,选择第1维度(y轴)进行分割。
构建过程如下:
- 根节点:(7,2)
- 左子树:(5,4)
- 左子树:(2,3)
- 右子树:(4,7)
- 右子树:(8,1)
- 右子树:(9,6)
- 左子树:(5,4)
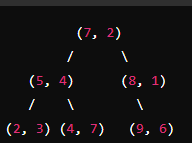
最近邻搜索
假设查询点是 (9,2),我们要找到距离这个点最近的点。
-
从根节点开始搜索:
- 根节点为 (7,2),查询点在第0维度上(x轴)的值大于7,因此向右子树搜索。
-
递归搜索右子树:
- 右子树根节点为 (8,1),查询点在第1维度上(y轴)的值大于1,因此向右子树搜索。
-
到达叶节点:
- 右子树根节点为 (9,6),这是一个叶节点。
-
回溯检查:
- 计算当前最近点的距离,(9,6) 到 (9,2) 的距离为 4。
- 回溯到父节点 (8,1),计算 (8,1) 到 (9,2) 的距离为 2,更新最近点为 (8,1)。
- 检查左子树的可能性,在第1维度上(y轴),查询点与分割点 (8,1) 的差值为 1,比当前最近点的距离 2 小,因此需要检查左子树。
- 由于左子树为空,继续回溯到根节点 (7,2) ,计算 (7,2) 到 (9,2) 的距离为 2,但当前最近点 (8,1) 的距离也为 2,所以不更新最近点。
- 在第0维度上(x轴),查询点与根节点的差值为 2,与当前最近点的距离相等,因此需要检查左子树。
- 左子树根节点为 (5,4),计算距离 (5,4) 到 (9,2) 的距离为 4,不更新最近点。
最终,我们找到的最近邻点是 (8,1)。
另一个kdtree实例: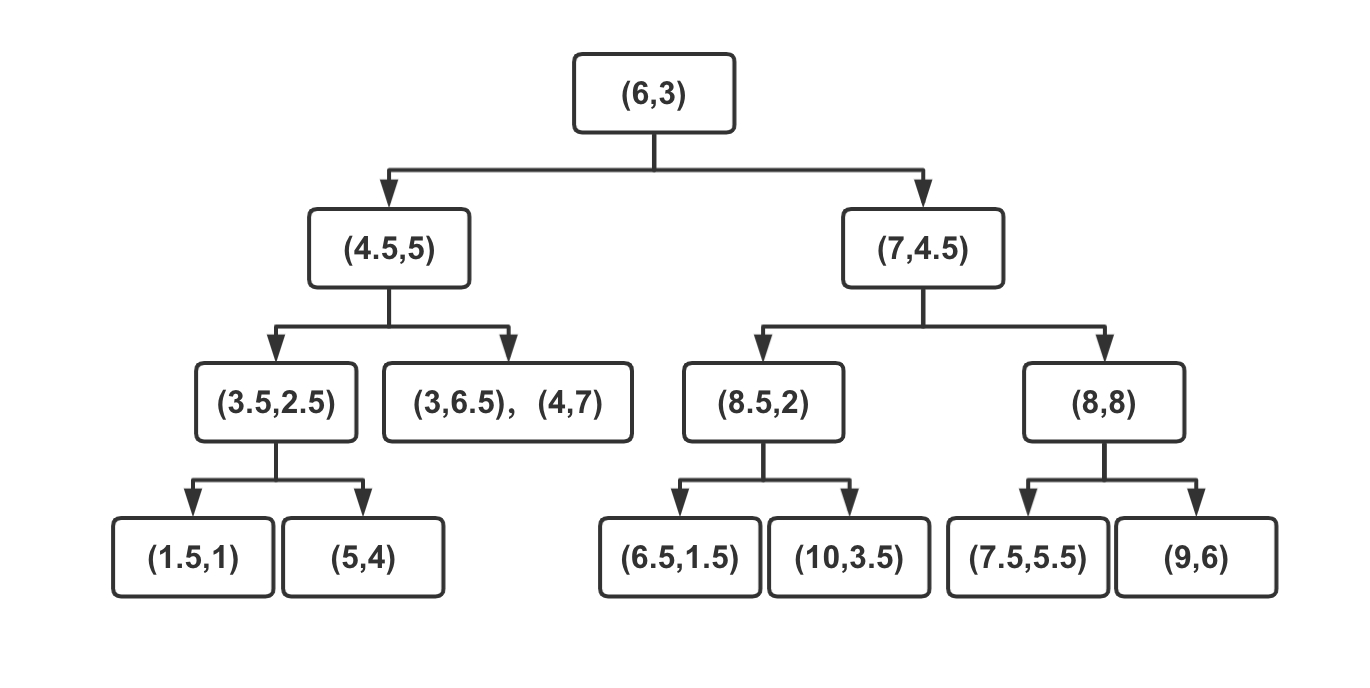
Ball tree
Ball Tree(球树)是一种用于高维空间的数据结构,主要用于高效的邻近搜索,如最近邻搜索(nearest neighbor search)和范围搜索(range search)。与 KD-Tree 不同,Ball Tree 使用球体(球形区域)来划分数据空间,从而在高维空间中提供更高效的搜索性能。
Ball Tree 的基本原理
Ball Tree 通过递归地将数据点划分为两个子集,子集中的每个节点都被包围在一个球体内。每个节点存储该球体的中心和半径,从而形成一种层次结构,便于高效搜索。
1. 构建 Ball Tree
Ball Tree 的构建过程是递归的,主要步骤如下:
- 选择分割点:选择当前节点的分割点(球体中心),通常是数据点的质心或中位数。
- 计算半径:计算当前节点的半径,使其包围所有数据点。
- 划分数据点:将数据点划分为两个子集,使得每个子集包含的点数大致相等。
- 递归构建子树:对每个子集递归构建左子树和右子树。
2. Ball Tree 的搜索
最近邻搜索
- 从根节点开始搜索:比较目标点与当前节点的距离,确定搜索的子树。
- 递归搜索子树:根据比较结果递归搜索左子树或右子树。
- 回溯检查其他子树:在回溯过程中,检查另一个子树是否有可能包含更近的点。如果有可能,则递归检查该子树。
更详细的实现过程需要参考以下文章中的代码实现逻辑:
机器学习算法系列(二十一)-k近邻算法(k-Nearest Neighbor / kNN Algorithm)-CSDN博客
class ballnode:
"""
ball 树结点
"""
def __init__(self, value, index, radius, left = None, right = None):
# 结点对应训练集的特征值;当结点为叶子结点时,为特征向量
self.value = value
# 结点对应训练集的下标;当结点为叶子结点时,为下标向量
self.index = index
# 超球体的半径
self.radius = radius
# 左子树
self.left = left
# 右子树
self.right = right
class balltree:
"""
ball 树算法实现
参数
----------
X : 特征矩阵
leaf_size : 叶子节点包含的最大特征矩阵数量,默认为 10
p : 距离范数,默认为 2,即欧式距离
"""
def __init__(self, X, leaf_size = 10, p = 2):
def build_node(X, X_indexes, leaf_size):
"""
构建结点
参数
----------
X : 特征矩阵
X_indexes : 特征矩阵下标
leaf_size : 叶子节点包含的最大特征矩阵数量
"""
# 当前特征矩阵的大小小于等于指定的叶子结点包含的特征矩阵数量时构建叶子结点并返回
if X.shape[0] <= leaf_size:
return ballnode(X, X_indexes, None)
# 距离最宽的维度(标准差越大,代表该维度下样本点之间差距有大)
feature = np.argmax(np.std(X, axis=0))
# 该维度下最大的样本点
X_feature_max = X[np.argmin(X[:, feature])]
# 该维度下最小的样本点
X_feature_min = X[np.argmax(X[:, feature])]
# 中心点
X_feature_median = (X_feature_max + X_feature_min) / 2
# 每个样本点与中心点之间的最大距离
radius = np.max(distance(X, X_feature_median, p))
# 将样本点分成两类
left_index = (distance(X, X_feature_max, p) - distance(X, X_feature_min, p)) < 0
if left_index.any():
# 递归的构建左子树
left = build_node(X[left_index, :], X_indexes[left_index], leaf_size)
right_index = ~left_index
if right_index.any():
# 递归的构建右子树
right = build_node(X[right_index, :], X_indexes[right_index], leaf_size)
# 构建当前结点并返回
return ballnode(X_feature_median, None, radius, left, right)
# 根结点
self.root = build_node(X, np.array(range(X.shape[0])), leaf_size)
def query(self, X, k = 1, p = 2):
"""
查询距离最近 k 个特征向量
参数
----------
X : 特征矩阵
k : 最近邻的数量,默认为 1
p : 距离范数,默认为 2,即欧式距离
"""
# 最近邻对应的下标向量
nearests = -np.ones((len(X), k), dtype = np.int8)
# 最近邻对应的距离向量
distances = -np.ones((len(X), k))
return self.search(X, self.root, nearests, distances, p)
def search(self, X, node, nearests, distances, p = 2):
"""
搜索距离最近 k 个特征向量
"""
# 当前结点不是叶子结点时
if node.left is not None or node.right is not None:
# 最大的距离
max_distance = np.max(distances, axis=1)
# 样本点与当前结点对应的超球面最近的距离大于当前的最大距离时,其子结点不可能存在跟近的距离,直接跳过
over = ((distance(X, node.value, p) - node.radius - max_distance) >= 0) & (distances != -1).all()
if over.all():
return nearests, distances
unover = ~over
# 递归搜索左子数
nearests[unover, :], distances[unover, :] = self.search(X[unover, :], node.left, nearests[unover, :], distances[unover, :], p)
# 递归搜索右子数
nearests[unover, :], distances[unover, :] = self.search(X[unover, :], node.right, nearests[unover, :], distances[unover, :], p)
else:
# 依次遍历当前叶子结点包含的特征向量
for i in range(len(node.value)):
# 更新下标与距离记录的方式 k-d 树
dist = distance(X, node.value[i], p)
all_cond = np.zeros((X.shape[0],), dtype=np.bool)
for j in range(nearests.shape[1]):
cond = (~all_cond) & ((distances[:, j] < 0) | (dist - distances[:, j] < 0))
if (~cond).all():
continue
ns = np.insert(nearests[cond, :], j, node.index[i], axis=1)
nearests[cond, :] = ns[:,:-1]
ds = np.insert(distances[cond, :], j, dist[cond], axis=1)
distances[cond, :] = ds[:,:-1]
all_cond = all_cond | cond
if all_cond.all():
break
return nearests, distances
另一种搜索近邻的树 :
kdtree搜索效率为什么低于balltree
1. 数据分布与维度的影响
KD-Tree
KD-Tree 通过递归地将数据空间沿着每个维度的中位数进行分割,形成一个平衡的二叉树。然而,这种分割方式在高维空间中可能会导致以下问题:
- 维度诅咒:随着维度数的增加,KD-Tree 的效率显著下降。这是因为在高维空间中,数据点往往非常稀疏,导致大部分空间被划分为空区域,从而增加了搜索的复杂度。
- 非均匀数据分布:如果数据分布不均匀,KD-Tree 的分割方式可能导致树结构不平衡,从而增加了搜索时间。
Ball Tree
Ball Tree 通过递归地将数据点分成两个子集,使每个子集包含的点数大致相等,并用球体来包围这些子集。这种分割方式在高维空间和非均匀数据分布情况下更为有效:
- 灵活的空间划分:Ball Tree 的球体分割方式在高维空间中更具灵活性,能够更好地适应数据点的分布,从而减少了搜索的复杂度。
- 适应性更强:Ball Tree 能够更有效地处理非均匀数据分布,使得树结构更加平衡,从而提高了搜索效率。
2. 搜索剪枝策略
KD-Tree
在进行最近邻搜索时,KD-Tree 需要检查多个维度的边界条件,这使得剪枝策略较为复杂。在高维空间中,很多节点无法有效地剪枝,从而增加了搜索的时间。
Ball Tree
Ball Tree 通过计算查询点与球体边界的距离来进行剪枝。如果查询点与球体边界的距离大于当前已知的最近距离,则可以直接剪枝。这种剪枝策略在高维空间中更加高效,因为它只需要计算球体边界的距离,而不需要检查多个维度的边界条件。
3. 球体分割的优势
Ball Tree 使用球体来包围数据点,这种分割方式在高维空间中有更好的空间利用率。球体的分割方式使得查询点在球体内的搜索路径更加简洁,有助于提高搜索效率。
KNN的核心算法kd-tree和ball-tree - 简书 (jianshu.com)
13. K-means
深入理解K-Means聚类算法_k-means算法-CSDN博客
K-Means是一种广泛使用的聚类算法,用于将数据点分成K个簇,使得同一簇内的点之间的相似度最大,不同簇之间的点的相似度最小。它是一种迭代优化算法,具体步骤如下:
K-Means 算法步骤
- 选择初始质心:随机选择K个初始质心(centroids)。
- 分配数据点:将每个数据点分配到离它最近的质心,形成K个簇。
- 更新质心:计算每个簇的质心,将质心更新为该簇内所有数据点的平均值。
- 重复步骤2和3:直到质心不再发生变化或达到最大迭代次数。
K-Means 算法的具体步骤
1. 选择初始质心
随机选择K个点作为初始质心。质心是簇的中心点,通常选择数据点中的随机K个点。
2. 分配数据点
将每个数据点分配到离它最近的质心。距离通常使用欧几里得距离计算:
![]()
其中,xi是数据点,cj 是质心,d是维度数。
3. 更新质心
对于每个簇,计算所有数据点的平均值,更新质心的位置。计算公式为:
![]()
其中,Cj 是第j个簇,∣Cj∣ 是第j个簇中的数据点数量。
4. 重复步骤2和3
重复分配数据点和更新质心,直到质心不再发生变化或达到最大迭代次数。
python实现
import numpy as np
import matplotlib.pyplot as plt
def initialize_centroids(X, K):
# 随机选择K个初始质心
centroids = X[np.random.choice(X.shape[0], K, replace=False)]
return centroids
def assign_clusters(X, centroids):
# 分配数据点到最近的质心
distances = np.sqrt(((X - centroids[:, np.newaxis])**2).sum(axis=2))
clusters = np.argmin(distances, axis=0)
return clusters
def update_centroids(X, clusters, K):
# 更新质心
new_centroids = np.array([X[clusters == k].mean(axis=0) for k in range(K)])
return new_centroids
def kmeans(X, K, max_iters=100):
# 初始化质心
centroids = initialize_centroids(X, K)
for i in range(max_iters):
# 分配数据点
clusters = assign_clusters(X, centroids)
# 更新质心
new_centroids = update_centroids(X, clusters, K)
# 如果质心不再变化,停止迭代
if np.all(centroids == new_centroids):
break
centroids = new_centroids
return centroids, clusters
# 示例数据
X = np.array([
[1, 2], [1, 4], [1, 0],
[10, 2], [10, 4], [10, 0]
])
# 设置簇的数量
K = 2
# 运行K-Means算法
centroids, clusters = kmeans(X, K)
# 可视化结果
for i in range(K):
points = X[clusters == i]
plt.scatter(points[:, 0], points[:, 1], label=f'Cluster {i+1}')
plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='red', label='Centroids')
plt.legend()
plt.show()
与KNN对比
Kmeans算法与KNN算法的区别 - 白开水加糖 - 博客园 (cnblogs.com)
如何确定 K 值
1. 肘部法(Elbow Method)
肘部法通过计算不同 K 值下的聚类误差平方和(SSE),并绘制 SSE 随 K 值变化的图形。选择图中 SSE 曲线出现拐点的位置作为 K 值。
2. 轮廓系数法(Silhouette Method)
轮廓系数法计算不同 K 值下的轮廓系数(Silhouette Coefficient),选择轮廓系数最大的 K 值。轮廓系数是一个介于 -1 和 1 之间的值,值越大表示聚类效果越好。
K-Means 的迭代循环停止条件
- 质心不再变化:当前迭代更新后的质心与前一次迭代的质心相同,即质心位置不再变化。
- 达到最大迭代次数:设置一个最大迭代次数,如果达到这个次数仍未收敛,则停止迭代。
评判聚类效果的准则
1. 误差平方和(SSE)
SSE 衡量的是每个数据点到其所属簇质心的距离的平方和,反映了簇内数据点的紧密度。SSE 越小,表示簇内数据点越紧密,聚类效果越好。
2. 轮廓系数(Silhouette Coefficient)
轮廓系数综合考虑了簇内数据点的紧密度和簇间数据点的分离度。计算公式为:
![]()
其中:
- a 是数据点与其所在簇内其他点的平均距离。
- b 是数据点与最近簇内点的平均距离。
轮廓系数介于 -1 和 1 之间,值越大表示聚类效果越好。
3. 互信息(Mutual Information)
用于评估聚类结果与真实标签之间的相似度。互信息越大,表示聚类结果与真实分类越接近。
14. EM算法(Expectation-Maximization)
一种用于估计具有潜在变量的统计模型参数的迭代方法。它特别适用于处理数据中的隐变量或缺失数据的情况下,例如高斯混合模型(Gaussian Mixture Models,GMM)的参数估计。
EM 算法的基本步骤
EM 算法由两步组成:期望步(E-step)和最大化步(M-step),通过交替执行这两步来最大化似然函数。
- 初始化:对模型参数进行初始化。
- 期望步(E-step):根据当前参数估计,计算隐变量的期望值(即隐变量的后验概率)。
- 最大化步(M-step):最大化期望的对数似然函数,更新模型参数。
- 重复 E-step 和 M-step,直到参数收敛或达到最大迭代次数。
算法推导
目标函数:对数似然函数
给定观测数据 和隐变量
,我们希望最大化观测数据的对数似然函数:
![]()
其中,θ 是模型的参数。
由于直接最大化对数似然函数通常很难计算,EM 算法通过引入隐变量的概率分布 q(Z),将其转换为更容易优化的形式。
引入对数似然函数的下界
我们使用 Jensen 不等式,将对数似然函数的期望值分解为两个部分:
![]()
不等式右侧是对数似然函数的下界,也称为:
![]()
EM 算法的两个步骤
期望步骤(E-step)
在 E-step 中,我们固定当前参数 θ(t),最大化 以找到最优的隐变量概率分布 q(Z)。我们最大化
关于q的部分。最优解是使q等于后验概率p(Z|X, θ):
![]()
这意味着在 E-step 中,我们计算隐变量 Z 的后验概率。
最大化步骤(M-step)
在 M-step 中,我们固定 q(Z) 并最大化 以更新参数 θ。由于
可以进一步分解为:
![]()
其中第二项是熵,与 θ 无关,因此我们只需要最大化第一项:
![]()
EM 算法的推导总结
通过交替执行 E-step 和 M-step,我们可以不断优化参数 θ:
- E-step:计算隐变量的后验概率
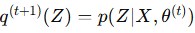 。
。 - M-step:更新参数

EM两步收敛性证明略,以上过程都可参考:【大道至简】机器学习算法之EM算法(Expectation Maximization Algorithm)详解(附代码)---通俗理解EM算法。-CSDN博客
高斯混合模型中的 EM 算法推导
高斯混合模型(GMM)是 EM 算法的典型应用场景。假设我们有 K 个高斯分布,每个高斯分布的参数为 ![]() ,混合系数为
,混合系数为 。
初始化
随机初始化 GMM 的参数 。
期望步骤(E-step)
计算第 i 个数据点属于第 k 个高斯分布的后验概率(责任度 ):
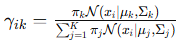
最大化步骤(M-step)
更新 GMM 的参数:
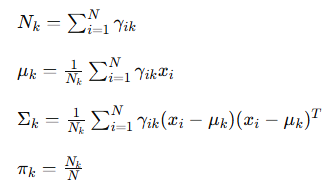
GMM实例

紫色点的含义
紫色点表示这些数据点在两个高斯分布之间的责任度接近于平均值。这意味着这些点的后验概率分布在两个高斯分布之间比较均衡。具体来说:
- 如果一个数据点在红色高斯分布中的责任度
和在蓝色高斯分布中的责任度
都接近 0.5,那么这个点在图中就会呈现紫色。
- 这表示这个点在两个高斯分布之间的边界附近,它们对这个点的贡献相当。
具体示例
假设我们有一个包含6个二维数据点的数据集:
X={(1,2),(2,3),(3,4),(5,6),(6,7),(8,9)}
我们希望用两个高斯分布(K=2)来拟合这些数据。
初始化
- 混合系数 πk:假设初始值为
,
。
- 均值 μk:假设初始值为
,
。
- 协方差矩阵 Σk:假设初始值为
。
E 步
计算每个数据点属于每个高斯分布的后验概率(责任度 )。
计算第一个数据点 (1,2)
计算第一个高斯分布的概率密度函数值:
计算第二个高斯分布的概率密度函数值:
计算责任度 和
:
对于其他数据点,我们同样计算 值。
M 步
更新 GMM 的参数。
计算 Nk:
更新均值 μk:
更新协方差矩阵 Σk:
更新混合系数 πk:
15. GMM(Gaussian Mixture Model)
高斯混合模型(GMM)聚类是一种软聚类方法,它假设数据是由多个高斯分布混合生成的。与K-Means这种硬聚类方法不同,GMM 允许一个数据点同时属于多个簇,并通过概率的形式来表达这种隶属关系。每个数据点在每个簇中的隶属程度由后验概率(责任度)表示。
聚类步骤见14.
新数据预测
步骤
- 计算每个高斯分布的概率密度函数值:对于新数据点 xxx,计算它在每个高斯分布下的概率密度函数值
。
- 计算后验概率(责任度):使用贝叶斯公式计算新数据点属于每个高斯分布的后验概率
- 确定最大后验概率:新数据点被分配到具有最大后验概率的高斯分布簇。
公式
对于新数据点 x,计算其在第 k 个高斯分布下的后验概率:
![]()
其中:
- πk是第 k 个高斯分布的混合系数。
是第 k 个高斯分布的概率密度函数值。
估计数据点概率(密度)
给定一个数据点 x,其在高斯混合模型下的生成概率(密度)可以表示为:
![]()
其中:
- K 是高斯分布的数量。
- πk 是第 k 个高斯分布的混合系数。
是第 k 个高斯分布的概率密度函数值。
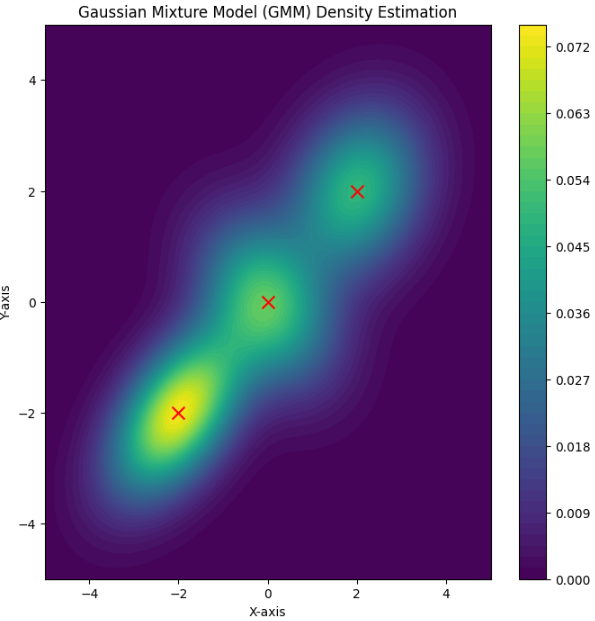
深度探索:机器学习中的高斯混合模型(GMM)原理及其应用-CSDN博客

 16. 隐马尔可夫模型(Hidden Markov Model, HMM)
16. 隐马尔可夫模型(Hidden Markov Model, HMM)
是一种统计模型,用于描述一个由隐藏的状态序列生成的可观测序列。HMM 常用于时间序列数据分析、语音识别、自然语言处理等领域。HMM 由两个主要序列组成:隐藏状态序列和观测序列。模型通过状态转移概率和观测概率描述状态之间的转换和观测的生成。
组成部分
一个 HMM 由以下几个部分组成:
- 状态集(State Space):假设有 N 个可能的隐藏状态,状态集合表示为
- 观测集(Observation Space):假设有 M 个可能的观测,观测集合表示为
- 初始状态概率(Initial State Probabilities):初始状态概率分布
,其中 πi 是初始状态为 Si 的概率。
- 状态转移概率(State Transition Probabilities):状态转移概率矩阵
,其中
是状态从 Si 转移到 Sj 的概率。
- 观测概率(Observation Probabilities):观测概率矩阵
,其中
是在状态 Si 下生成观测 Oj 的概率。
HMM 的三个基本问题
- 评估问题(Evaluation Problem):给定 HMM 模型参数和一个观测序列,计算得到该观测序列的概率。
- 解码问题(Decoding Problem):给定 HMM 模型参数和一个观测序列,找到最可能的隐藏状态序列。
- 学习问题(Learning Problem):给定一个观测序列,估计 HMM 的模型参数。
解决方法
- 前向算法(Forward Algorithm):用于解决评估问题。
- 维特比算法(Viterbi Algorithm):用于解决解码问题。
- Baum-Welch 算法:用于解决学习问题。
符号解释
状态相关
- S: 隐藏状态的集合,表示所有可能的隐藏状态。
- N: 隐藏状态的数量。
- qt: 在时间 t 的隐藏状态。
- πi: 初始状态概率,表示系统在时间 t=1时处于状态 Si 的概率。
观测相关
- O: 观测序列,表示实际可观测到的序列。
- M: 观测值的数量。
- Ot: 在时间 t 的观测值。
: 在状态 Sj 下生成观测值 Ot 的概率。
模型参数
- λ: HMM 的参数集合,包括初始状态概率 π、状态转移概率矩阵 A 和观测概率矩阵 B。
- A: 状态转移概率矩阵,
,其中
表示从状态 Si 转移到状态 Sj 的概率。
- B: 观测概率矩阵,
,其中
表示在状态 Si 下生成观测值 Oj 的概率。
前向算法(Forward Algorithm)
前向算法用于计算给定观测序列的概率。定义 为在时间 t 时,状态为 Si 并观测到前 t 个观测的联合概率,公式定义:
![]()
递推关系: 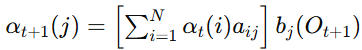
- αt+1(j): 在时间 t+1 时,状态为 Sj 并观测到前 t+1 个观测值的联合概率。
- ∑i=1Nαt(i)aij\sum_{i=1}^N \alpha_t(i) a_{ij}∑i=1Nαt(i)aij: 在时间 ttt 时的所有状态 SiS_iSi 转移到状态 SjS_jSj 的概率和。
- bj(Ot+1)b_j(O_{t+1})bj(Ot+1): 在状态 SjS_jSj 下生成观测值 Ot+1O_{t+1}Ot+1 的概率。
初始条件: ![]()
观测序列概率: ![]()
维特比算法(Viterbi Algorithm)
维特比算法用于找到最可能的隐藏状态序列。定义 为在时间 t 时,最可能的状态序列的概率,并且该序列的最后一个状态是 Si,定义:
![]()
递推关系: ![]()
- δt+1(j): 在时间 t+1 时,以状态 Sj 结尾的最可能的隐藏状态序列的概率。
: 时间 ttt 时所有状态 Si 转移到状态 Sj 的最大概率。
: 在状态 Sj 下生成观测值
的概率。
初始条件: ![]()
- δ1(i): 在时间 t=1 时,以状态 Si 结尾的最可能的隐藏状态序列的概率。
- πi: 初始状态 Si 的概率。
: 在状态 Si 下生成观测值 O1 的概率。
最可能的隐藏状态序列的概率: ![]()
最终条件和回溯
- P∗: 最可能的隐藏状态序列的概率。
- Q∗: 最可能的隐藏状态序列。
: 记录在时间 t 状态 Sj 的最优路径来自于哪一个状态 Si。
通过递推计算 和
,在时间 T 时选择最大
对应的状态,并回溯
来找到最可能的隐藏状态序列。
Baum-Welch 算法
Baum-Welch 算法用于估计 HMM 的参数。它是一种基于期望最大化(EM)算法的迭代过程。主要包括以下步骤:
-
计算
和
:
表示在时间 t 时状态为 Si 的概率。
表示在时间 t 时状态为 Si 且在时间 t+1时状态为 Sj 的概率。
-
更新参数:
- 更新初始状态概率:
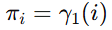
- 更新状态转移概率:

- 更新观测概率:
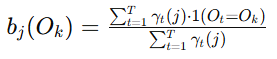
- 更新初始状态概率:
计算实例
HMM 模型参数
-
状态集(S):{晴天(Sunny), 雨天(Rainy)}
-
观测集(O):{散步(Walk), 购物(Shop), 清洁(Clean)}
-
初始状态概率分布(π\piπ):π=[0.6,0.4],表示初始时晴天的概率为0.6,雨天的概率为0.4
-
状态转移概率矩阵(A):

其中
表示从状态 Si 转移到状态 Sj 的概率
-
观测概率矩阵(B):

其中
表示在状态 Si 下生成观测 Oj 的概率
假设我们有以下观测序列:O=[散步,购物,清洁]
1. 前向算法
我们将使用前向算法计算观测序列的概率。
初始化
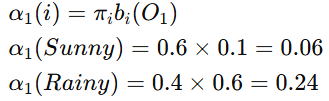
递推
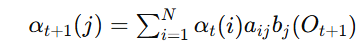
时间 t=2 时:
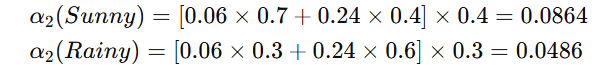
时间 t=3 时:
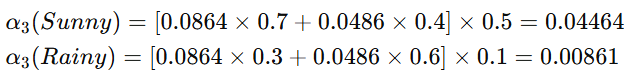
终止
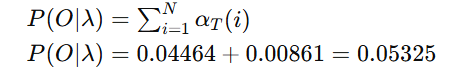
2. 维特比算法
我们将使用维特比算法找到最可能的隐藏状态序列。
初始化
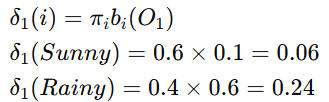
递推
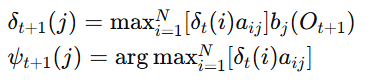
时间 t=2 时:
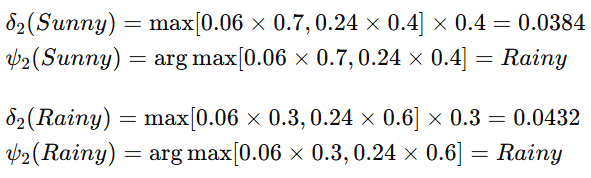
时间 t=3t=3t=3 时:

终止和回溯
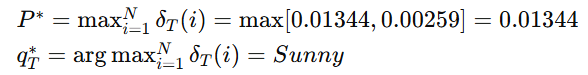
回溯: 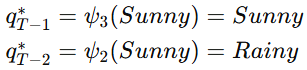
最可能的隐藏状态序列为:[Rainy, Sunny, Sunny]
17. 一些指标(Accuracy、Precision、Recall和 F1 Score。。。)
True positives(TP,真正) : 预测为正,实际为正
True negatives(TN,真负):预测为负,实际为负
False positives(FP,假正): 预测为正,实际为负
False negatives(FN,假负): 预测为负,实际为正
TPR(true positive rate,真正类率)
TPR = TP/(TP+FN)
真正类率TPR代表分类器预测的正类中实际正实例占所有正实例的比例。
FPR(false positive rate,假正类率)
FPR = FP/(FP+TN)
假正类率FPR代表分类器预测的正类中实际负实例占所有负实例的比例。
低FPR表示模型很少误报负例为正例。
TNR(ture negative rate,真负类率)特异性(Specificity)
TNR = TN/(FP+TN)
真负类率TNR代表分类器预测的负类中实际负实例占所有负实例的比例。
- 高特异性表示模型能够识别大多数负例。
- 适用于希望减少假阳性的场景。
FNR (False Negative Rate,假阴率)
![]()
- 低FNR表示模型很少漏掉正例。
Accuracy
ACC = (TP+TN)/(TP+TN+FN+FP)
评判标准:
- 高准确率表示大多数预测是正确的。
- 适用于正负样本数量大致相等的情况。不适用于极度不平衡的数据集,因为在这种情况下,高准确率可能只是由于对大多数负例的正确预测,而忽略了正例。
Precision
P = TP/(TP+FP)
![]()
表示当前划分到正样本类别中,被正确分类的比例(正确正样本所占比例)。
评判标准:
- 高精确率意味着少有假正例(FP),即模型预测为正例的样本中大多数确实是正例。
- 精确率较高时适用于假阳性代价较高的场景,例如疾病诊断中不希望健康人被误诊为病人。
Recall
R = TP/(TP+FN)
![]()
表示当前划分到正样本类别中,真实正样本占所有正样本的比例。
评判标准:
- 高召回率意味着少有假反例(FN),即模型能够识别出大多数正例。
- 召回率较高时适用于假阴性代价较高的场景,例如网络安全中不希望漏掉任何入侵行为。
F-score
F-score可以被推广为Fβ-score,其中β是一个调整精确率和召回率权重的参数。具体来说:
![]()
-
当β=1时,F1-score,意味着精确率和召回率的权重相同:

-
当β>1时,Fβ-score对召回率给予更多的权重。
-
当β<1时,Fβ-score对精确率给予更多的权重。
评判标准:
- F1-score是精确率和召回率的调和平均数,适用于需要平衡这两者的重要性时。
- 高F1-score表示模型在精确率和召回率之间找到了较好的平衡。
ROC曲线(接收者操作特性曲线)
ROC曲线是通过绘制不同阈值下的真阳率(True Positive Rate, TPR)与假阳率(False Positive Rate, FPR)来评估分类器的性能。
-
真阳率(TPR, 召回率):

-
假阳率(FPR):
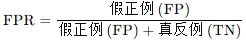
AUC值(曲线下面积)
AUC(Area Under the Curve)是ROC曲线下的面积,用于衡量分类器的整体性能。AUC值越接近1,分类器性能越好。
AUC-ROC的直观解释
AUC值可以解释为:从所有正例和所有负例中随机抽取一个正例和一个负例,分类器将正例的得分判为高于负例的概率。举例来说:
- AUC = 0.9 表示,如果我们随机抽取一个正例和一个负例,模型有90%的概率将正例的得分判为高于负例的得分。
评判标准:
- AUC值范围从0.5到1.0。值越接近1.0,模型性能越好。
- AUC = 0.5 表示模型没有预测能力,与随机猜测相同。
- 0.7 ≤ AUC < 0.8 表示模型性能一般。
- 0.8 ≤ AUC < 0.9 表示模型性能良好。
- AUC ≥ 0.9 表示模型性能非常好。
PR曲线(精确率-召回率曲线)
PR曲线是通过绘制不同阈值下的精确率(Precision)与召回率(Recall)来评估分类器的性能。
评判标准:
- PR AUC越高,表示模型在不平衡数据集上性能越好。
- PR AUC特别适用于数据集中的正负样本比例严重不平衡的情况。
区别
- ROC曲线和AUC值:适用于不平衡数据集,但会被大量的真反例(TN)影响。
- PR曲线:在处理不平衡数据集时更有效,特别是当关注正例(Positive)时。
- 无论测试集中的正负样本比例如何变化,这些TPR和FPR值只依赖于模型本身的表现,不依赖于正负样本的数量,因此ROC曲线保持不变。
- 与此不同,PR曲线会随着正负样本的分布变化而变化。这是因为精确率(Precision)受假正例(FP)的影响,当测试集中的正负样本比例变化时,精确率也会随之变化。
机器学习之分类器性能指标之ROC曲线、AUC值 - dzl_ML - 博客园 (cnblogs.com)
18. 一些问题
梯度弥散(Gradient Vanishing)
现象
在梯度弥散问题中,反向传播过程中,梯度逐层传递时逐渐变小,最终在某些层几乎变为零。这会导致这些层的权重几乎不更新,模型难以训练。
原因
梯度弥散通常发生在深度神经网络中,当激活函数的导数小于1时(如sigmoid和tanh)。在多次连乘后,梯度会指数级减小,最终导致梯度趋近于零。
影响
- 深层网络的前几层几乎不学习,无法有效调整权重。
- 训练过程变得非常缓慢,甚至无法收敛。
解决方法
- 使用合适的激活函数:例如ReLU(Rectified Linear Unit)和其变种(如Leaky ReLU、ELU)等,这些函数在大部分输入区间的导数为1,可以有效缓解梯度弥散问题。
- 权重初始化:使用He初始化或Xavier初始化等方法,可以帮助权重在初始时具有适当的尺度,从而缓解梯度弥散。
- 批归一化(Batch Normalization):通过对每一层的输入进行归一化,保持数据分布的稳定,有助于缓解梯度弥散问题。
梯度爆炸(Gradient Explosion)
现象
在梯度爆炸问题中,反向传播过程中,梯度逐层传递时逐渐变大,最终在某些层变得非常大。这会导致权重更新幅度过大,训练过程不稳定。
原因
梯度爆炸通常发生在深度神经网络中,当激活函数的导数大于1时(如ReLU的部分输入区间),或当权重初始化不当时。在多次连乘后,梯度会指数级增大,最终导致梯度变得非常大。
影响
- 权重更新过大,导致模型无法收敛。
- 训练过程变得非常不稳定,损失函数可能会发生剧烈波动。
解决方法
- 梯度裁剪(Gradient Clipping):在反向传播时对梯度进行裁剪,使其保持在一个合理的范围内,从而避免梯度过大。
- 权重初始化:使用合适的初始化方法(如Xavier初始化和He初始化),避免初始权重过大导致的梯度爆炸。
- 学习率调整:使用较小的学习率,或者采用学习率衰减策略,避免权重更新幅度过大。
例子:简单的深度神经网络
假设我们有一个非常简单的深度神经网络,包含4层,每层有一个神经元,并且我们使用sigmoid激活函数。
神经网络结构
- 输入层: x
- 隐藏层1: h1=σ(W1x+b1)h_1 = \sigma(W_1 x + b_1)h1=σ(W1x+b1)
- 隐藏层2: h2=σ(W2h1+b2)h_2 = \sigma(W_2 h_1 + b_2)h2=σ(W2h1+b2)
- 隐藏层3: h3=σ(W3h2+b3)h_3 = \sigma(W_3 h_2 + b_3)h3=σ(W3h2+b3)
- 输出层: y=σ(W4h3+b4)y = \sigma(W_4 h_3 + b_4)y=σ(W4h3+b4)
其中,σ 是sigmoid激活函数,W 是权重矩阵,b 是偏置。
Sigmoid激活函数及其导数
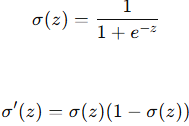
反向传播中的梯度计算
在反向传播中,我们需要计算损失函数对每个权重的梯度。假设我们的损失函数是均方误差(MSE),定义为:
![]()
我们需要计算每层权重的梯度,以便进行更新:
假设损失函数对输出层的导数是: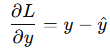
梯度弥散推导
为了简化推导过程,我们只考虑每层的梯度链式法则:

其中,z4=W4h3+b4z_4 = W_4 h_3 + b_4z4=W4h3+b4,我们有:
∂y∂z4=σ′(z4)\frac{\partial y}{\partial z_4} = \sigma'(z_4)∂z4∂y=σ′(z4)
类似地,计算前一层的梯度:
∂L∂W3=∂L∂h3⋅∂h3∂z3⋅∂z3∂W3\frac{\partial L}{\partial W_3} = \frac{\partial L}{\partial h_3} \cdot \frac{\partial h_3}{\partial z_3} \cdot \frac{\partial z_3}{\partial W_3}∂W3∂L=∂h3∂L⋅∂z3∂h3⋅∂W3∂z3 ∂h3∂z3=σ′(z3)\frac{\partial h_3}{\partial z_3} = \sigma'(z_3)∂z3∂h3=σ′(z3)
在每一层,梯度都会乘以一个小于1的数(sigmoid的导数在0到1之间)。假设每层的导数平均值约为0.1,那么通过每一层时,梯度都会变为原来的10%。例如:
- 第4层到第3层:梯度变为原来的10%
- 第3层到第2层:梯度变为原来的1%
- 第2层到第1层:梯度变为原来的0.1%
这样,梯度在反向传播过程中逐渐减小,最终接近于零,这就是梯度弥散。
梯度爆炸推导
我们来看梯度爆炸的问题。如果激活函数是ReLU或其他在某些区间导数大于1的函数,权重初始化过大,导致每层的导数都大于1,那么梯度在反向传播过程中会逐渐增大。
假设每层的导数平均值约为3,那么通过每一层时,梯度都会变为原来的3倍。例如:
- 第4层到第3层:梯度变为原来的3倍
- 第3层到第2层:梯度变为原来的9倍
- 第2层到第1层:梯度变为原来的27倍
这样,梯度在反向传播过程中逐渐增大,最终变得非常大,这就是梯度爆炸。
KL 散度和交叉熵的区别
交叉熵(Cross-Entropy)
定义
交叉熵是用来衡量两个概率分布之间差异的一种度量。假设我们有一个真实的分布 PPP 和一个模型预测的分布 QQQ,那么交叉熵定义为:
H(P,Q)=−∑xP(x)logQ(x)H(P, Q) = -\sum_{x} P(x) \log Q(x)H(P,Q)=−x∑P(x)logQ(x)
解释
- 直观解释:交叉熵衡量的是用分布 QQQ 来表示分布 PPP 时所需要的额外信息量。
- 应用:在机器学习中,交叉熵通常用于分类任务中的损失函数,特别是在多分类问题中,用于衡量模型预测的概率分布和真实类别分布之间的差异。
KL 散度(Kullback-Leibler Divergence)
定义
KL 散度是用来衡量两个概率分布 PPP 和 QQQ 之间的差异的一种非对称度量。定义如下:
DKL(P∥Q)=∑xP(x)logP(x)Q(x)D_{KL}(P \parallel Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}DKL(P∥Q)=x∑P(x)logQ(x)P(x)
解释
- 直观解释:KL 散度衡量的是从分布 QQQ 到分布 PPP 的信息损失。它表示的是如果我们用分布 QQQ 来近似分布 PPP 时,额外需要多少信息。
- 性质:KL 散度是非对称的,即 DKL(P∥Q)≠DKL(Q∥P)D_{KL}(P \parallel Q) \neq D_{KL}(Q \parallel P)DKL(P∥Q)=DKL(Q∥P)。
区别和联系
- 公式关系:
交叉熵 H(P,Q)H(P, Q)H(P,Q) 可以分解为分布 PPP 的熵 H(P)H(P)H(P) 和 KL 散度 DKL(P∥Q)D_{KL}(P \parallel Q)DKL(P∥Q) 的和:
H(P,Q)=H(P)+DKL(P∥Q)H(P, Q) = H(P) + D_{KL}(P \parallel Q)H(P,Q)=H(P)+DKL(P∥Q)
其中,熵 H(P)H(P)H(P) 是分布 PPP 的自信息量,表示的是分布 PPP 自身的不确定性:
H(P)=−∑xP(x)logP(x)H(P) = -\sum_{x} P(x) \log P(x)H(P)=−x∑P(x)logP(x)
所以,交叉熵可以看作是分布 PPP 的熵和分布 PPP 与分布 QQQ 之间的 KL 散度的和。
- 用途:
- 交叉熵:在机器学习中,交叉熵通常用作损失函数。它直接衡量模型预测的概率分布与真实分布之间的差异。
- KL 散度:更多用于理论分析,衡量两个分布之间的差异,通常用在变分推断、生成对抗网络(GAN)等领域。
- 对称性:
- 交叉熵:对 PPP 和 QQQ 是非对称的,因为它涉及到 QQQ 的对数。
- KL 散度:对 PPP 和 QQQ 也是非对称的,表示的是从一个分布到另一个分布的方向性信息损失。
梯度下降陷入局部最优有什么解决办法
1. 使用不同的初始化方法
初始化方法会影响模型训练的结果,使用更好的初始化方法可以帮助避免局部最优解。
- 随机初始化:采用随机数进行参数初始化。
- Xavier初始化:适用于Sigmoid和Tanh激活函数,权重初始化为一个均匀分布或正态分布,其方差依赖于输入和输出层的节点数。
- He初始化:适用于ReLU激活函数,权重初始化为一个正态分布,其方差依赖于输入层的节点数。
2. 使用动量方法
动量方法通过在更新梯度时考虑之前的梯度来加速收敛,并减少震荡。
3. 使用高级优化算法
高级优化算法可以帮助克服局部最优问题:
- Adam(Adaptive Moment Estimation):结合了动量和自适应学习率的优点。
- RMSprop:自适应调整每个参数的学习率。
- Adagrad:为每个参数分配不同的学习率,适用于稀疏数据。
4. 学习率调整
调整学习率可以帮助模型跳出局部最优:
- 学习率衰减:逐渐降低学习率,可以帮助模型在接近最优解时稳定收敛。
- 循环学习率(Cyclic Learning Rate):在训练过程中周期性地调整学习率。
5. 使用批归一化(Batch Normalization)
批归一化可以使模型训练更稳定,帮助跳出局部最优。
6. 数据增强
通过增加训练数据的多样性,可以帮助模型更好地学习特征,减少过拟合,并提高泛化能力。
7. 使用模拟退火(Simulated Annealing)
模拟退火是一种概率性跳出局部最优的方法,它在训练初期允许较大的跳跃,并逐渐减少跳跃幅度。
8. 添加噪声
在梯度更新中添加噪声,可能帮助模型跳出局部最优。
9. 集成学习(Ensemble Learning)
通过训练多个模型,并将它们的预测结果结合起来,可以提高模型的稳定性和性能。
如何解决正负样本数量不均衡?
1. 数据层面的解决方法
过采样(Oversampling)
过采样是通过增加少数类样本的数量来平衡数据集。常见的方法有:
- 随机过采样:随机重复少数类样本,直到数量与多数类相等。
- SMOTE(Synthetic Minority Over-sampling Technique):通过插值的方法生成新的少数类样本。
欠采样(Undersampling)
欠采样是通过减少多数类样本的数量来平衡数据集。常见的方法有:
- 随机欠采样:随机删除多数类样本,直到数量与少数类相等。
数据增强
通过对少数类样本进行数据增强(如旋转、缩放、裁剪等),增加少数类样本的多样性,从而平衡数据集。
2. 模型层面的解决方法
类别权重调整
在训练模型时,给少数类样本赋予更大的权重,使模型在训练过程中更加关注少数类样本。
- 在损失函数中加入权重:
- 在深度学习中使用权重交叉熵损失:
平衡分类器(Balanced Classifier)
一些分类算法天然支持不均衡数据集,例如:
- 平衡随机森林:在每棵树的训练中进行欠采样。
- 平衡提升(Balanced Boosting):在每次迭代中调整样本权重,使分类器更关注难分类的少数类样本。
3. 评估层面的调整
在不均衡数据集中,仅使用准确率来评估模型性能是不够的,应采用更加全面的评估指标:
- 混淆矩阵:了解模型的详细分类结果。
- 精确率(Precision)和召回率(Recall):分别衡量模型对正类预测的准确性和覆盖率。
- F1-score:精确率和召回率的调和平均数。
- ROC曲线和AUC值:评估模型在不同阈值下的分类性能。
- PR曲线(Precision-Recall Curve):特别适用于不均衡数据集的评估。
如何加快梯度下降收敛速度
1. 学习率调整
动态学习率
- 学习率衰减:逐步减少学习率,可以避免训练后期过大的更新步伐导致的震荡。常见的衰减方式包括阶梯衰减、指数衰减和余弦衰减。
- 自适应学习率方法:例如AdaGrad、RMSprop、Adam等优化算法,会根据参数更新的历史信息自动调整学习率。
2. 动量方法
经典动量
- 动量梯度下降:在梯度更新中引入动量项,利用历史梯度信息加速收敛并减少震荡。 vt+1=γvt+η∇J(θt)v_{t+1} = \gamma v_t + \eta \nabla J(\theta_t)vt+1=γvt+η∇J(θt) θt+1=θt−vt+1\theta_{t+1} = \theta_t - v_{t+1}θt+1=θt−vt+1 其中,γ\gammaγ 是动量因子,η\etaη 是学习率。
3. 高级优化算法
- Adam(Adaptive Moment Estimation):结合了AdaGrad和RMSprop的优点,计算每个参数的自适应学习率。
- Nadam:结合了Adam和Nesterov动量方法。
4. 批归一化(Batch Normalization)
- 批归一化:在每层激活函数之前对输入数据进行归一化处理,减小内部协变量偏移,加快模型收敛。 x^(k)=x(k)−μBσB2+ϵ\hat{x}^{(k)} = \frac{x^{(k)} - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}x^(k)=σB2+ϵx(k)−μB 其中,μB\mu_BμB 和 σB2\sigma_B^2σB2 分别是小批量数据的均值和方差,ϵ\epsilonϵ 是一个很小的数,防止分母为零。
5. 权重初始化
- Xavier初始化:适用于Sigmoid和Tanh激活函数,将权重初始化为一个均匀分布或正态分布,其方差依赖于输入和输出层的节点数。
- He初始化:适用于ReLU激活函数,权重初始化为一个正态分布,其方差依赖于输入层的节点数。
6. 提前停止(Early Stopping)
- 提前停止:在验证集上的损失在一定次数后不再减少时,提前终止训练,防止过拟合和减少训练时间。
7. 数据增强和正则化
- 数据增强:通过在训练过程中对训练数据进行随机变换(如旋转、缩放、裁剪等),增加训练数据的多样性,提高模型的泛化能力。
- 正则化:如L2正则化(权重衰减),可以防止模型过拟合,从而加快收敛。
信息熵
信息熵(通常简称为熵)是对一个随机变量的不确定性的一种度量。它告诉我们在某个系统中平均需要多少比特来表示一个事件的发生。
通俗解释
猜硬币游戏
假设你在玩一个猜硬币正反面的游戏。硬币有两个面:正面(H)和反面(T)。
-
公平的硬币:
- 如果硬币是公平的(每次抛硬币出现正面和反面的概率都是50%),你不知道硬币下一次是正面还是反面。
- 这种情况下的不确定性最大,信息熵也最大。
- 信息熵计算:−0.5log2(0.5)−0.5log2(0.5)=1-0.5 \log_2(0.5) - 0.5 \log_2(0.5) = 1−0.5log2(0.5)−0.5log2(0.5)=1 比特。
-
不公平的硬币:
- 如果硬币是不公平的(比如90%概率是正面,10%概率是反面),你猜到硬币下一次是正面的概率更高,不确定性减少了。
- 这种情况下的信息熵较低。
- 信息熵计算:−0.9log2(0.9)−0.1log2(0.1)≈0.47-0.9 \log_2(0.9) - 0.1 \log_2(0.1) \approx 0.47−0.9log2(0.9)−0.1log2(0.1)≈0.47 比特。
字母猜测游戏
另一个例子是猜测一个字母的游戏。如果你要猜测一个字母,但你知道这个字母可能性很高是 'e'(在英语中最常用的字母),那么你的不确定性较小,信息熵也较小。
信息熵公式
假设我们有一个离散随机变量 XXX ,它有 nnn 个可能的取值,每个取值的概率分别是 p1,p2,...,pnp_1, p_2, ..., p_np1,p2,...,pn。信息熵 H(X)H(X)H(X) 定义为:
H(X)=−∑i=1npilog2(pi)H(X) = -\sum_{i=1}^n p_i \log_2(p_i)H(X)=−i=1∑npilog2(pi)
直观理解
- 高熵:意味着系统中有很多不确定性。比如在抛公平硬币时,你不知道下一个结果是什么。
- 低熵:意味着系统中有较少不确定性。比如在抛不公平硬币时,你能比较确定下一个结果。
信息熵在机器学习中的应用
在机器学习中,信息熵常用于决策树的构建。决策树使用熵来决定如何分割数据,使得每次分割后数据的不确定性(熵)尽可能减少,从而提高模型的分类准确性。
Softmax是和什么loss function配合使用?
Softmax函数定义
给定一个包含 nnn 个实数的向量 z=[z1,z2,...,zn]\mathbf{z} = [z_1, z_2, ..., z_n]z=[z1,z2,...,zn],Softmax函数将其转换为一个概率分布。具体定义如下:
softmax(zi)=ezi∑j=1nezj\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}}softmax(zi)=∑j=1nezjezi
其中, eee 是自然对数的底, ziz_izi 是向量 z\mathbf{z}z 的第 iii 个元素。
特点
- 非负性:Softmax函数的输出为非负数。
- 归一化:Softmax函数的输出和为1,表示一个有效的概率分布。
- 平滑性:Softmax函数的输出随输入的变化平滑变化,适合多分类问题的概率预测。
例子
假设我们有一个包含三个元素的向量 z=[2.0,1.0,0.1]\mathbf{z} = [2.0, 1.0, 0.1]z=[2.0,1.0,0.1],我们来计算其Softmax值:
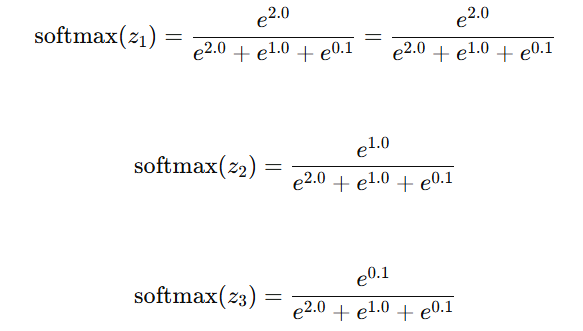
交叉熵损失函数(Cross-Entropy Loss)
交叉熵损失函数用于衡量两个概率分布之间的差异。在多分类问题中,它计算模型预测的概率分布和实际类别分布(通常是独热编码)的交叉熵。
定义
假设我们有 nnn 个类别,真实标签 yyy 使用独热编码表示,模型预测的概率分布为 y^\hat{y}y^。交叉熵损失的公式为:
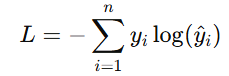
其中, yiy_iyi 是实际类别的独热编码, y^i\hat{y}_iy^i 是模型预测的概率。
为什么Softmax和交叉熵损失函数一起使用?
- 概率分布:Softmax函数将模型输出转换为概率分布,总和为1,适合作为多分类问题的预测输出。
- 损失计算:交叉熵损失函数用于衡量实际类别分布与预测概率分布之间的差异,指导模型优化。
交叉熵损失的工作原理
- 独热编码:交叉熵损失函数将实际标签转换为独热编码。
- Softmax:在计算交叉熵损失之前,损失函数内部会对模型的输出应用Softmax函数。
- 损失计算:计算实际标签分布和预测概率分布之间的交叉熵。
这样,模型在训练过程中可以最小化交叉熵损失,从而提高分类性能。







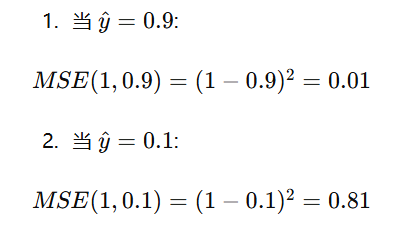





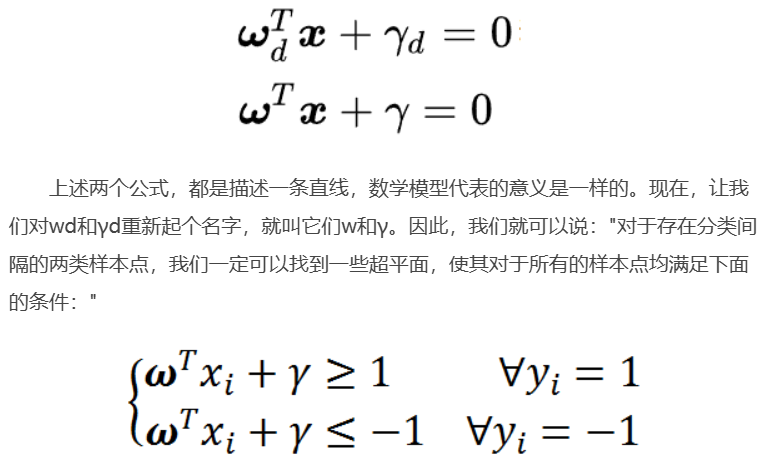
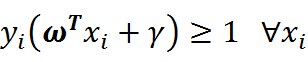
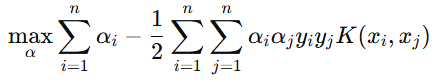

















 9954
9954

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








