算法设计技巧
参考 : 《数据结构与算法分析 Java语言描述》. Mark Allen Weiss. 机械工业出版社
第十章 : 算法设计技巧
贪心算法(贪婪算法)
-
贪婪算法分阶段工作,在每一阶段,选择局部最优解,在算法终止时,希望获得全局最优解。
-
问题 : 给定 N N N 个作业 j 1 , j 2 , … , j N j_1 , j_2 ,\dots, j_N j1,j2,…,jN ,其运行时间分别是 t 1 , t 2 , … , t N t_1 , t_2 , \dots, t_N t1,t2,…,tN ,处理器只有一个。
- 如何调度这些作业使得作业的平均完成时间最短?
多处理器情况
问题 : 给定 N N N 个作业 j 1 , j 2 , … , j N j_1 , j_2 ,\dots, j_N j1,j2,…,jN ,其运行时间分别是 t 1 , t 2 , … , t N t_1 , t_2 , \dots, t_N t1,t2,…,tN ,处理器多个。
比如有3个处理器同时工作,下面是每个作业执行的时间,完成这些作业需要最少的时间是多少?

-
一种情况:完成需要40个单位时间

-
另一种情况:完成需要38个单位时间

-
最佳的完成时间需要34个单位时间

-
Minimizing the Final Completion Time 最后完成时间最小化
-
即各处理器之间如何更平均地承担任务
-
用更少的时间完成更多的任务。
-
属于NP Hard 问题
活动选择问题
- 活动选择问题:在一系列给出的活动中选出一个最大兼容活动子集(数目最多)。
- 例如 : 以下示例中,子集 { a 3 , a 9 , a 11 } \{a_3, a_9, a_{11}\} {a3,a9,a11}是一个解,然而最优解是 { a 1 , a 4 , a 8 , a 11 } \{a_1, a_4, a_8, a_{11}\} {a1,a4,a8,a11} ,或 { a 2 , a 4 , a 9 , a 11 } \{a_2, a_4, a_9, a_{11}\} {a2,a4,a9,a11},最优解的大小为4。
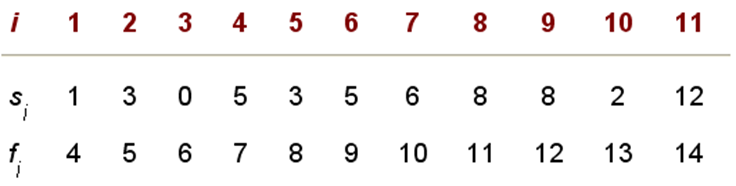
注: s i s_i si为(start)开始时间 , f i f_i fi为(finish)结束时间
活动选择问题(加权)
- 活动选择问题(加权):给定一系列活动 a i a_i ai,其对应的开始时间为 s i s_i si,结束时间为 f i f_i fi,每个活动还有一个对应的权值 v i v_i vi(价值),问题是需要找出若干个相容的活动,使得总的权值最大。

递归解
- 定义
O
P
T
(
j
)
OPT(j)
OPT(j)为活动
{
1
,
2
,
…
,
j
}
\{1, 2, \dots,j \}
{1,2,…,j}上的最优解,则有:
- O P T ( j ) = m a x ( v j + O P T ( p ( j ) ) , O P T ( j − 1 ) ) OPT(j) = max(v_j+OPT(p(j)),OPT(j-1)) OPT(j)=max(vj+OPT(p(j)),OPT(j−1))
独立集问题
-
独立集问题 : 设 G = ( V , E ) G = (V, E) G=(V,E) 是一个简单无向图, S S S是 V V V的子集,若 S S S中的节点在图 G G G中都无边相连,则称 S S S是一个独立集。在普通图中要找出最大独立集是非常困难的。在下面两图中黄色点构成极大独立集,上图中的极大独立集为9,下图中的极大独立集为8。
-

-

树上的独立集问题
- 在一些特殊图要快速找出最大独立集是可以做到的。在下图中标出你做的选择,并给出做出这些选择的理由。换句话说,你能否证明你选出的就是一个最大独立集。

- 贪心算法求解
- 定理 : 如果 T = ( V , E ) T=(V, E) T=(V,E)是一棵树, v v v是 T T T的一片树叶,那么存在包含 v v v 的最大独立集。
- 贪心算法:考虑一条边 e = ( u , v ) e=(u, v) e=(u,v),其中 v v v是树叶,独立集 S S S将包含节点 v v v,而不包含节点 u u u,做出这个决定后,则可以删除节点 v v v和节点 u u u,得到一棵小一些的树,继续在这棵剩下的树上重复前面的策略。
问题定义:设树 T = ( V , E ) T=(V, E) T=(V,E),每一个节点 v v v关联一个正的权 w w w,请在树 T T T中找出一个独立集 S S S,使得 S S S中包含的节点的权之和最大。
-

-
问题的关键:对于节点 u u u和与它相邻的树叶构成的子树,实际上只存在两种选择,即要么选择 u u u,要么选择所有的树叶。
-
考虑以节点 u u u为根构成的子树,最终的独立集 S S S要么包含 u u u,则不能包含它的任何一个孩子节点;要么不包含 u u u,则有包含或删去这些孩子节点的自由。
-
树上最大权独立集的递归式
- O P T i n ( u ) = w u + ∑ v ∈ c h i l d r e n ( u ) O P T o u t ( v ) OPT_{in}(u)=w_u+\sum\limits_{v\in children(u)}OPT_{out}(v) OPTin(u)=wu+v∈children(u)∑OPTout(v)
- O P T o u t ( u ) = ∑ v ∈ c h i l d r e n ( u ) m a x ( O P T o u t ( v ) , O P T i n ( v ) ) OPT_{out}(u) = \sum\limits_{v\in children(u)} max(OPT_{out}(v),OPT_{in}(v)) OPTout(u)=v∈children(u)∑max(OPTout(v),OPTin(v))
-
自底向上求解
装箱问题
- 装箱问题(Bin Packing) : 给定 N N N 项物品,大小为 S 1 , S 2 … , S N S_1 ,S_2…,S_N S1,S2…,SN,所有的大小都满足 0 < S i < = 1 0<S_i<=1 0<Si<=1。问题是要把这些物品装到最小数目的箱子中去,已知每个箱子的容量是 1 1 1个单位。
- 如图所示把大小为 0.2 , 0.5 , 0.4 , 0.7 , 0.1 , 0.3 , 0.8 0.2, 0.5, 0.4, 0.7, 0.1, 0. 3, 0.8 0.2,0.5,0.4,0.7,0.1,0.3,0.8 的一列物品最优装箱的方法。

联机和脱机
-
有两个版本的装箱问题
- 第一种是联机装箱问题( on-line bin packing problem)。在这种问题中,每一件物品必须放入一个箱子之后才能处理下一件物品。
- 第二种是脱机装箱问题(off-line bin packing problem)。在一个脱机装箱算法中,我们做任何事都可以等到所有的输入数据全被读取之后才进行。
-
联机算法的局限性 —— 不存在最优算法
- 为了证明联机算法不总能够给出最优解,我们将给它一组特别难的数据来处理。考虑由权为 1 2 − ε \frac{1}{2}-\varepsilon 21−ε 的 M M M 个小项和其后权为 1 2 + ε \frac{1}{2}+\varepsilon 21+ε 的 M M M 个大项构成的序列 L 1 L1 L1,其中 0 < ε < 0.01 0 < \varepsilon < 0.01 0<ε<0.01。显然,如果我们在每个箱子中放一个小项再放一个大项,那么这些项物品可以放入到 M M M 个箱子中去。 ( 1 2 − ε ) × M + ( 1 2 + ε ) × M = M (\frac{1}{2}-\varepsilon)\times M+ (\frac{1}{2}+\varepsilon)\times M=M (21−ε)×M+(21+ε)×M=M
- 假设存在一个最优联机算法 A A A 可以进行这项装箱工作。考虑算法 A A A 对序列 L 2 L2 L2的操作,该序列只由权为 1 2 − ε \frac{1}{2}-\varepsilon 21−ε 的 M M M 个小项组成。 L 2 L2 L2是可以装入 M / 2 M/2 M/2个箱子中的。然而,由于 A A A 对序列 L 2 L2 L2处理结果必然和对 L 1 L1 L1 的前半部分处理结果相同,而 L 1 L1 L1 前半部分的输入跟 L 2 L2 L2 的输入完全相同,因此, A A A 将把每一项物品放到一个单独的箱子内,即箱子没装满。这说明 A A A 将使用 L 2 L2 L2 最优解的两倍多的箱子(原本只需要 M 2 \frac{M}{2} 2M个箱子,现在要 M M M个箱子装)。这样我们证明了,对于联机装箱问题不存在最优算法。
-
联机算法的局限性—— 不存在太好的近似算法
-
定理 :存在使得任意联机装箱算法至少使用4/3最优箱子数的输入。
-
证明(反证法):假设情况相反。即存在算法 A A A使用少于 4 / 3 4/3 4/3最优箱子数完成装箱。
-
(1)设序列 L L L有 M M M个小项后接 M M M个大项组成 (为简单起见并设 M M M是偶数, 且规定一个箱子最多只能放一个小项和一个大项) 。考虑任一运行在上面输入序列 I 1 I_1 I1上的联机算法 A A A, 让我们考虑该算法在处理第 M M M 项后都做了什么。设 A A A 已经用了 b b b 个箱子。在算法的这一时刻(即处理了第 M M M项之后),箱子的最优个数是 M / 2 M/2 M/2 , 因为我们可以在每个箱子里放入两件物品。于是我们知道,根据优于 4 / 3 4/3 4/3 最优箱子数的性能保证的假设, 这时已用的箱子占全部装满的箱子的个数比例 b M 2 = 2 b / M < 4 / 3 \frac{b}{\frac{M}{2}} =2b/M <4/3 2Mb=2b/M<4/3。
-
(2)现在考虑在所有的物品都被装箱后算法 A A A 的性能。在第 b b b 个箱子之后开辟的所有箱子的每箱恰好包含一项物品,因为所有小项物品都被放在了前 b b b 个箱子中,而两个大项物品又装不进一个箱子中去。由于前b 个箱子每箱最多能有两项物品,而其余的箱子每箱都有一项物品,因此我们看到,将 2 M 2M 2M 项物品 (大项加小项) 装箱将至少需要 2 M − b 2M-b 2M−b (即 2 M − 2 b + b 2M-2b+b 2M−2b+b)个箱子。但 2 M 2M 2M 项物品可以用** M M M 个箱子最优装箱**,因此我们的性能保障保证得到 ( 2 M − b ) / M < 4 / 3 (2M-b)/M < 4/3 (2M−b)/M<4/3。
-
在(1)中意味着 b / M < 2 / 3 b/M <2/3 b/M<2/3,在(2)中意味着 b / M > 2 / 3 b/M>2/3 b/M>2/3,这是矛盾的。因此,没有联机算法能够保证使用小于 4 / 3 4/3 4/3的最优装箱数完成装箱。因此要使(1)和(2)中的条件成立, b / M = 2 / 3 b/M=2/3 b/M=2/3即可,即 ( 2 M − b ) / M = 4 / 3 (2M-b)/M = 4/3 (2M−b)/M=4/3
-
-
有三种简单算法保证所用的箱子数不多于二倍的最优装箱数。也有很多更为复杂的算法能够得到更好的结果。
近似在线装箱算法
- 下项适应算法 (next fit) : 大概最简单的算法就属下项适合(next fit) 算法了。当处理任何一项物品时,我们检查看它是否还能装进刚刚装进物品的同一个箱子中去。如果能够装进去,那么就把它放入该箱中;否则,就开辟一个新的箱子。这个算法实现起来出奇地简单,而且还以线性时间运行。
- 大白话 就是在上一次装的箱子里看是否能装下,装得下就装,装不下就拿新的空箱子装。
- 定理 : 令 M M M 是将一列物品 L L L 装箱所需的最优装箱数,则下项适合算法所用箱数决不超过 2 M 2M 2M 个箱子。存在一些顺序使得下项适合算法用箱数达 2 M − 2 2M -2 2M−2 个

- 首次适应算法 (first fit) : 首次适合算法(first fit) 的策略是依序扫描这些箱子并把新的一项物品放入足能盛下它的第一个箱子中。因此,只有当前面那些放置物品的箱子已经容不下当前物品的时候,我们才开辟一个新箱子。
- 大白话 就是在下项适应算法的基础上,通过回去找之前没有装满的箱子,看看是否还能装下目前的东西。而下项适应算法只是在上一次装东西的箱子中找是否能装得下,如果装不下就不会再往前面的箱子找,而是去新开辟一个空箱来装。
- 定理 : 令 M M M 是将一列物品 L L L 装箱所需要的最优箱子数,则首次适合算法使用的箱子数决不多于 ⌈ 17 10 M ⌉ \lceil \frac{17}{10}M \rceil ⌈1017M⌉。存在使得首次适合算告使用 ⌈ 17 10 ( M − 1 ) ⌉ \lceil \frac{17}{10}(M-1) \rceil ⌈1017(M−1)⌉ 个箱子的序列。

- 最佳适应算法 (best fit) : 该算法不是把一项新物品放入所发现的第一个能够容纳它的箱子,而是放到所有箱子中能够容纳它的最满的箱子中。
- 大白话 就是在首次适应算法的基础上,找出剩余空间最小并且能容纳下当前物品的箱子, 比如下图中的 B 2 B_2 B2箱子 和 B 3 B_3 B3的箱子,可以看出当放入东西为0.3前, B 2 B_2 B2剩余0.6, 但 B 3 B_3 B3剩余0.3, 即 B 3 B_3 B3刚好剩余最小且能容纳它,这就是最佳适应算法,这样的好处就是 B 2 B_2 B2就能腾出大的空间放大东西。 而使用首次适应算法, 就会放在 B 2 B_2 B2那个箱子里, 它是根据顺序进行放的,这样的缺点是不能保证每次箱子剩下的容量是最大的, 但最佳适应算法一定能保证最后每次箱子剩下的都是最大的空间,这样下次放东西的时候减少因为容量不够而去开辟新的空间的次数,从而减少箱子个数。

脱机算法
- **如果我们能够观察全部物品以后再算出答案,那么我们应该会做得更好。**事实确实如此,由于我们通过彻底的搜索最终能够找到最优装箱方法,因此我们对联机情形就已经有了一个理论上的改进。
- 所有联机算法的主要问题在于将大项物品装箱困难,特别是当它们在输入的后期出现的时候。围绕这个问题的自然方法是将各项物品排序,把最大的物品放在最先。此时我们可以应用首次适合算法或最佳适合算法,分别得到首次适合递减算法(first fit decreasing)和最佳适合递减算法(best fit decreasing) 。
- 首次适合递减算法
- 定理 : 令 M M M 是将物品集 L L L 装箱所需的最优箱子数,则首次适合递减算法所用箱子数决不超过 ( 4 M + 1 ) / 3 (4M + 1)/3 (4M+1)/3。
- 定理 : 令 M M M 是将物品集L 装箱所需的最优箱数,则首次适合递减算法所用箱数决不超过 11 9 M + 4 \frac{11}{9}M+4 911M+4。此外,存在使得首次适合递减算法用到 11 9 M \frac{11}{9}M 911M 个箱子的序列。

分治算法
用于设计算法的另一种常用技巧为分治算法( divide and conquer)。分治算法由两部分组成 :
- 分(divide) : 递归解决较小的问题(当然,基本情况除外)。
- 治( conquer) : 然后从子问题的解构建原问题的解。
分治算法的运行时间
-
T ( N ) = 2 T ( N / 2 ) + O ( N ) , T ( 1 ) = 1 T(N)=2T(N/2)+O(N), T(1)=1 T(N)=2T(N/2)+O(N),T(1)=1
-
T ( N ) = 4 T ( N / 2 ) + O ( N ) T(N)=4T(N/2)+O(N) T(N)=4T(N/2)+O(N)
-
T ( N ) = 2 T ( N / 2 ) + O ( 1 ) T(N)=2T(N/2)+O(1) T(N)=2T(N/2)+O(1)
-
T ( N ) = T ( N − 1 ) + O ( 1 ) T(N)=T(N-1)+O(1) T(N)=T(N−1)+O(1)
-
T ( N ) = 2 T ( N − 1 ) + O ( 1 ) T(N)=2T(N-1)+O(1) T(N)=2T(N−1)+O(1)
定理1 :
-
对于以下递归方程式
T ( N ) = a T ( N / b ) + Θ ( N k ) T(N) = a \ T(N / b) + \Theta(N^k) T(N)=a T(N/b)+Θ(Nk), 其中 a ≥ 1 , b > 1 a \geq 1, b > 1 a≥1,b>1, 且 p ≥ 0 p \geq 0 p≥0 。该方程式的解为:
T ( N ) = { O ( N l o g b a ) , i f a > b k O ( N k l o g N ) , i f a = b k O ( N k ) , i f a < b k T(N)=\begin{cases}O(N^{log_b a}), \quad if \ a>b^k \\O(N^klogN), \quad if\ a=b^k \\ O(N^k),\quad if \ a<b^k \end{cases} T(N)=⎩⎪⎨⎪⎧O(Nlogba),if a>bkO(NklogN),if a=bkO(Nk),if a<bk
定理2 :
-
对于以下递归方程式
T ( N ) = a T ( N / b ) + Θ ( N k l o g p N ) T(N) = a \ T(N / b) + \Theta(N^k \ log^p N) T(N)=a T(N/b)+Θ(Nk logpN), 其中 a ≥ 1 , b > 1 a \geq 1, b > 1 a≥1,b>1, 且 p ≥ 0 p \geq 0 p≥0 。该方程式的解为:
T ( N ) = { O ( N l o g b a ) , i f a > b k O ( N k l o g p + 1 N ) , i f a = b k O ( N k l o g p N ) , i f a < b k T(N)=\begin{cases}O(N^{log_b a}), \quad if \ a>b^k \\O(N^klog^{p+1}N), \quad if\ a=b^k \\ O(N^klog^pN),\quad if \ a<b^k \end{cases} T(N)=⎩⎪⎨⎪⎧O(Nlogba),if a>bkO(Nklogp+1N),if a=bkO(NklogpN),if a<bk
- 例如 : 归并排序 a = b = 2, p = 0 and k = 1. ⟹ \Longrightarrow ⟹ T = O ( N l o g N ) T = O(NlogN) T=O(NlogN)
- 注意 : l o g p N log^pN logpN 就是以2为底数的对数 l o g 2 p N log_2^p N log2pN, 计算机术语中默认省略2
定理3 :
- 若 ∑ i = 1 k a i < 1 \sum\limits_{i=1}^k a_i <1 i=1∑kai<1 , 则方程 T ( N ) = ∑ i = 1 k T ( a i N ) + O ( N ) = O ( N ) T(N)=\sum\limits_{i=1}^kT(a_i N)+O(N) = O(N) T(N)=i=1∑kT(aiN)+O(N)=O(N)
归并排序
- T ( N ) = 2 T ( N / 2 ) + O ( N ) T(N) = 2T(N/2)+O(N) T(N)=2T(N/2)+O(N)
选择问题
- 从一组未排序的数中选出第k大的数。
- T ( N ) = T ( N / 2 ) + N T(N)=T(N/2)+N T(N)=T(N/2)+N
最近点对问题
- 平面上有N个点,找出距离最近的两个点。


最近点对的分治
- 对所有点按 x x x坐标排序。画一条想象的垂线将点集分为两半 P L PL PL和 P R PR PR。那么最近点对要么出现在 P L PL PL中,要么出现在 P R PR PR中,要么跨越 P L PL PL和 P R PR PR。我们把这三个距离分别叫做 d L , d R , d C dL,dR,dC dL,dR,dC。 d L , d R dL,dR dL,dR可以递归计算,但 d C dC dC如何计算。另外,要想得到 O ( N l o g N ) O(NlogN) O(NlogN)算法,则 d C dC dC的计算代价最多为 O ( N ) O(N) O(N)。
- 考察条带中的点
- 对于均匀分布的点,平均只有 O ( N 1 2 ) O(N^{\frac{1}{2}}) O(N21)个点分布在这个条带中。因此使用蛮力法计算这 O ( N 1 2 ) O(N^{\frac{1}{2}}) O(N21)个点两两之间的距离也只需O(N)时间。

/* points are all in the strip */
for ( i=0; i<NumPointsInStrip; i++ )
for ( j=i+1; j<NumPointsInStrip; j++ )
if ( Dist( Pi , Pj ) < s )
s = Dist( Pi , Pj );
- 考察
y
y
y坐标
-
在 δ × δ \delta \times \delta δ×δ 的区域中,最多存在4个满足条件的点。即每两点之间的距离小于等于 δ \delta δ 。因此在 2 × δ × δ 2 \times \delta \times \delta 2×δ×δ 区域中最多存在8个满足条件的点。因此对于每个 p i p_i pi,最多考虑另外7个点即可。
-
-

-
/* points are all in the strip */
/* and sorted by y coordinates */
for ( i = 0; i < NumPointsInStrip; i++ )
for ( j = i + 1; j < NumPointsInStrip; j++ )
if ( Dist_y( Pi , Pj ) > s )
break;
else if ( Dist( Pi , Pj ) < s )
s = Dist( Pi , Pj );
整数相乘问题
- 两个 N N N位数 相乘,采用传统的竖式乘法,需要执行 N 2 N^2 N2 乘法。
- 整数相乘的改进
- 设
X
,
Y
X,Y
X,Y是两个
N
N
N位整数(为方便起见,设
N
=
2
k
N=2^k
N=2k),用
X
L
X_L
XL表示
X
X
X 的前半部分,
X
R
X_R
XR 表示
X
X
X的后半部分;用
Y
L
Y_L
YL表示
Y
Y
Y的前半部分,
Y
R
Y_R
YR表示
Y
Y
Y的后半部分;则:
- X Y = X L Y L 1 0 N + ( X L Y R + X R Y L ) 1 0 N / 2 + X R Y R XY= X_LY_L10^N + (X_LY_R + X_RY_L)10^{N/2} + X_RY_R XY=XLYL10N+(XLYR+XRYL)10N/2+XRYR
- 以上方程由四次乘法和三次加法构成,因此可得递归式: T ( N ) = 4 T ( N / 2 ) + O ( N ) T(N) = 4T(N/2)+O(N) T(N)=4T(N/2)+O(N)
- 根据[定理一](# 定理1 : ), ∵ a = 4 , b = 2 , k = 1 , a > b k , ∴ O ( N l o g 2 4 ) = O ( N 2 ) \because a=4, b=2,k=1, a>b^k, \ \therefore O(N^{log_24})=O(N^2) ∵a=4,b=2,k=1,a>bk, ∴O(Nlog24)=O(N2) 即 T ( N ) = O ( N 2 ) T(N) = O(N^2) T(N)=O(N2)
- 因此,关键是能否将以上递归式中的 “4” 变小。
- 对此有: X L Y R + X R Y L = ( X L − X R ) ( Y R − Y L ) + X L Y L + X R Y R X_LY_R + X_RY_L= (X_L-X_R)(Y_R-Y_L) + X_LY_L + X_RY_R XLYR+XRYL=(XL−XR)(YR−YL)+XLYL+XRYR 而 X L Y L X_LY_L XLYL和 X R Y R X_RY_R XRYR是已经计算过的。
- 因此,计算 X Y XY XY可以仅由三次一半规模的乘法和 O ( N ) O(N) O(N)次加减法来完成。所以递归式变为 T ( N ) = 3 T ( N / 2 ) + O ( N ) T(N) = 3T(N/2) + O(N) T(N)=3T(N/2)+O(N) 。根据[定理一](# 定理1 :)可知 ∵ a = 3 , b = 2 , k = 1 , a > b k , ∴ O ( N l o g 2 3 ) = O ( N 1.59 ) \because a=3, b=2,k=1, a>b^k, \ \therefore O(N^{log_23})=O(N^{1.59}) ∵a=3,b=2,k=1,a>bk, ∴O(Nlog23)=O(N1.59) ,算法的时间复杂度为 T ( N ) = O ( N l o g 2 3 ) = O ( N 1.59 ) T(N) = O(N^{log_23} ) = O(N^{1.59}) T(N)=O(Nlog23)=O(N1.59)。
- 设
X
,
Y
X,Y
X,Y是两个
N
N
N位整数(为方便起见,设
N
=
2
k
N=2^k
N=2k),用
X
L
X_L
XL表示
X
X
X 的前半部分,
X
R
X_R
XR 表示
X
X
X的后半部分;用
Y
L
Y_L
YL表示
Y
Y
Y的前半部分,
Y
R
Y_R
YR表示
Y
Y
Y的后半部分;则:
- 整数相乘的"三分"
- 分成三部分
- T ( N ) = 9 T ( N / 3 ) + O ( N ) T(N) = 9T(N/3) + O(N) T(N)=9T(N/3)+O(N)
- 相同方式下,它可以降低时间复杂度
- T ( N ) = 5 T ( N / 3 ) + O ( N ) T(N) = 5T(N/3) + O(N) T(N)=5T(N/3)+O(N)
矩阵乘法
- 两个 N N N阶矩阵 X X X和 Y Y Y相乘,最终得到一个 N N N阶矩阵 Z Z Z,矩阵 Z Z Z中有 N 2 N^2 N2个元素,每个元素需要花费 N N N次乘法和 N − 1 N-1 N−1次加法获得。因此传统的矩阵相乘的时间复杂度为 O ( N 3 ) O(N^3) O(N3) 。
- 矩阵乘法改进(Strassen)
-
与整数乘法类似的分治,采用分块相乘方法。需要8次 N / 2 N/2 N/2阶矩阵的乘法和4次 N / 2 N/2 N/2阶矩阵的加法。 N / 2 N/2 N/2阶矩阵有 N 2 / 4 N^2/4 N2/4个元素,因此加法所需运算为 O ( N 2 ) O(N^2) O(N2)。
-
因此有: T ( N ) = 8 T ( N / 2 ) + O ( N 2 ) T(N) = 8T(N/2) + O(N^2) T(N)=8T(N/2)+O(N2)
-
[ A 1 , 1 A 1 , 2 A 2 , 1 A 2 , 2 ] [ B 1 , 1 B 1 , 2 B 2 , 1 B 2 , 2 ] = [ C 1 , 1 C 1 , 2 C 2 , 1 C 2 , 2 ] \left[ \begin{matrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \end{matrix} \right] \left[ \begin{matrix} B_{1,1} & B_{1,2} \\ B_{2,1} & B_{2,2} \end{matrix} \right] =\left[ \begin{matrix} C_{1,1} & C_{1,2} \\ C_{2,1} & C_{2,2} \end{matrix} \right] [A1,1A2,1A1,2A2,2][B1,1B2,1B1,2B2,2]=[C1,1C2,1C1,2C2,2]
-
C 1 , 1 = A 1 , 1 B 1 , 1 + A 1 , 2 B 2 , 1 C 1 , 2 = A 1 , 1 B 1 , 2 + A 1 , 2 B 2 , 2 C 2 , 1 = A 2 , 1 B 1 , 1 + A 2 , 2 B 2 , 1 C 2 , 2 = A 2 , 1 B 1 , 2 + A 2 , 2 B 2 , 2 \begin {aligned}C_{1,1} &= A_{1,1} B_{1,1} \ + \ A_{1,2}B_{2,1} \\ C_{1,2} &= A_{1,1} B_{1,2} \ + \ A_{1,2}B_{2,2} \\ C_{2,1} &= A_{2,1} B_{1,1} \ + \ A_{2,2}B_{2,1} \\ C_{2,2} &= A_{2,1} B_{1,2} \ + \ A_{2,2}B_{2,2} \end {aligned} C1,1C1,2C2,1C2,2=A1,1B1,1 + A1,2B2,1=A1,1B1,2 + A1,2B2,2=A2,1B1,1 + A2,2B2,1=A2,1B1,2 + A2,2B2,2
-
若 T ( N ) = 8 T ( N / 2 ) + O ( N 2 ) T(N) = 8T(N/2) + O(N^2) T(N)=8T(N/2)+O(N2),根据 [定理一](# 定理1: )可知, T ( N ) = O ( N 3 ) T(N) = O(N^3) T(N)=O(N3)
-
因此关键问题也是如何将上式中的 “8” 缩小。
-
8次乘法的压缩, T ( N ) = 7 T ( N / 2 ) + O ( N 2 ) T(N) = 7T(N/2) + O(N^2) T(N)=7T(N/2)+O(N2)
-
T ( N ) = O ( N 2.81 ) T(N) = O(N^{2.81}) T(N)=O(N2.81)
-

-
-

-
动态规划
-
动态规划—Dynamic programming
-
动态规划中涉及到递归的处理。
-
Fibonacci Numbers: F ( N ) = F ( N – 1 ) + F ( N – 2 ) F(N) = F(N – 1) + F(N – 2) F(N)=F(N–1)+F(N–2)
int Fib( int N )
{
if ( N <= 1 )
return 1;
else
return Fib( N - 1 ) + Fib( N - 2 );
}
-
动态规划适用于子问题不是独立的情况,也就是各子问题包含公共的“子子问题”。动态规划对每个子子问题只求解一次,将其结果保存在一张表中,从而避免每次遇到各个子问题时重新计算答案。
-
通常应用于最优化问题,其步骤如下 :
-
- 描述最优解的结构;
- 递归定义最优解的值;
- 按自底向上的方式计算最优解的值;
- 由计算出的结果构造一个最优解。
-
动态规划基础
- 适合采用动态规划方法的最优化问题中的两个要素:
- (1)最优子结构
- (2)重叠子问题
- 应用动态规划的一种方法,称为备忘录(memoization),以充分利用重叠子问题性质。
最优子结构
- DP以自底向上的方式来利用最优子结构。即首先找到子问题的最优解,解决子问题,然后找到问题的一个最优解。寻找问题的一个最优解需要在子问题中做出选择,即选择将用哪一个来求解问题。问题解的代价通常是子问题的代价加上选择本身带来的开销。
重叠子问题
-
适用于DP求解的问题的第二个要素是“子问题”的空间要很小,即用来求解原问题的递归算法可反复地解同样的子问题,而不是总在产生新的子问题。典型地,不同的子问题数是输入规模的一个多项式。
-
DP算法总是充分利用重叠子问题,即通过每个子问题只解一次,把解保存在一个在需要时就可以查看的表中,而且每次查表的时间为常数。
低效的递归
- Fibonacci Numbers: F ( N ) = F ( N – 1 ) + F ( N – 2 ) F(N) = F(N – 1) + F(N – 2) F(N)=F(N–1)+F(N–2)
int Fib( int N )
{
if ( N <= 1 )
return 1;
else
return Fib( N - 1 ) + Fib( N - 2 );
}
更高效的递归
- 通过避免重复计算来优化递归

int Fibonacci ( int N )
{ int i, Last, NextToLast, Answer;
if ( N <= 1 ) return 1;
Last = NextToLast = 1; /* F(0) = F(1) = 1 */
for ( i = 2; i <= N; i++ ) {
Answer = Last + NextToLast; /* F(i) = F(i-1) + F(i-2) */
NextToLast = Last; Last = Answer; /* update F(i-1) and F(i-2) */
} /* end-for */
return Answer;
}
动态规划与贪心算法
- 加权活动选择问题
- 树上的最大权独立集
装配线调度
-
汽车工厂有两条装配线,每条有 n n n 个装配站。装配线 i i i 的第 j j j个装配站表示为 S i , j S_{i,j} Si,j,在该站的装配时间为 a i , j a_{i,j} ai,j 。汽车底盘进入装配线 i i i,花费时间为 e i e_i ei 。在通过一条线的第 j j j 个装配站后, 这个底盘可来到任一条装配线的第 ( j + 1 ) (j+1) (j+1)个装配站。如果它留在相同的装配线,则没有移动开销。但是,若它移动到另一条线上,则花费时间为 t i , j t_{i,j} ti,j 。在离开一条装配线的第 n n n 个装配站后,汽车底盘花费时间 x i x_i xi 离开工厂。
-
问题:确定应该在装配线 1 1 1 选择哪些站,在装配线 2 2 2 选择哪些站, 才能使汽车通过工厂的总时间最短。
-

-
装配线调度 —— 一个最优解
-

-
(1)最优解的结构
- 通过装配站 S i j S_{ij} Sij的最快路线包含了子问题,即通过前一个装配站的一个最优解。这个性质称为“最优子结构”,这是能否应用DP方法的标志之一。
- 通过建立子问题的最优解,就可以建立原问题的一个最优解。
-
(2)递归表达式
-
动态规划的第二个步骤就是利用子问题的最优解来递归定义一个最优解的值。
-
通过装配线1上的节点的最快时间:
-
通过装配线2上的节点的最快时间:
-
-
(3)计算最快时间
-
根据前面的两个递归式很容易得知计算该递归式的复杂度为 O ( 2 n ) O(2^n) O(2n)。
-
但是从递归式中也可以发现,很多计算是重复的,若从左到右进行计算则复杂度竟然是 O ( n ) O(n) O(n),这正是动态规划区别于分治法的关键之一。因为可以利用后面的计算可以利用子问题的计算结果。
-
Fastest Way —— 自底向上的计算
-

-
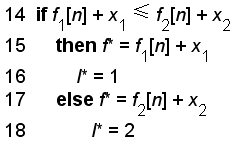
-
-
(4)构造经过的最快线路
- 按站号的递减顺序,输出所使用的各个装配站。

-
矩阵乘法的顺序安排
-
设 T n = T_n = Tn= 计算 M 1 ⋅ M 2 ⋯ M n M_1 \cdot M_2 \cdots M_n M1⋅M2⋯Mn的不同方法。则 T 2 = 1 , T 3 = 2 , T 4 = 5 , ⋯ T_2 = 1, T_3 = 2, T_4 = 5, \cdots T2=1,T3=2,T4=5,⋯
-
设 M i j = M i ⋯ M j M_{ij} = M_i \cdots M_j Mij=Mi⋯Mj. 则 M 1 n = M 1 ⋯ M n = M 1 i ⋯ M i + 1 n ⇒ T n = ∑ i = 1 n − 1 T i T n − i M_{1n} = M_1 \cdots M_n = M_{1i} \cdots M_{i+1 \ n} \Rightarrow T_n = \sum\limits_{i=1}^{n-1} T_iT_{n-i} M1n=M1⋯Mn=M1i⋯Mi+1 n⇒Tn=i=1∑n−1TiTn−i w h e r e n > 1 a n d T i = 1 where \ n>1 \ and \ T_i = 1 where n>1 and Ti=1
-
假设我们要乘 n n n 个矩阵 M 1 × ⋯ × M n M_1 \times \cdots \times M_n M1×⋯×Mn 其中 M i M_i Mi是一个 r i − 1 × r i r_{i-1} \times r_i ri−1×ri 矩阵。设 m i j m_{ij} mij为计算 M i × ⋯ × M j M_i \times \cdots \times M_j Mi×⋯×Mj的最优方法的成本。然后我们有递归方程:
-
不同 m i j m_{ij} mij 的个数为 N 2 N^2 N2。
/* r contains number of columns for each of the N matrices */
/* r[ 0 ] is the number of rows in matrix 1 */
/* Minimum number of multiplications is left in M[ 1 ][ N ] */
void OptMatrix( const long r[ ], int N, TwoDimArray M )
{ int i, k, Left, Right;
long ThisM;
for( Left = 1; Left <= N; Left++ ) M[ Left ][ Left ] = 0;
for( k = 1; k < N; k++ ) /* k = Right - Left */
for( Left = 1; Left <= N - k; Left++ ) { /* For each position */
Right = Left + k; M[ Left ][ Right ] = Infinity;
for( L = Left; L < Right; L++ ) {
ThisM = M[ Left ][ L ] + M[ L + 1 ][ Right ]
+ r[ Left - 1 ] * r[ L ] * r[ Right ];
if ( ThisM < M[ Left ][ Right ] ) /* Update min */
M[ Left ][ Right ] = ThisM;
} /* end for-L */
} /* end for-Left */
}
最优二叉查找树
- 给定 N N N 个单词 w 1 < w 2 < … … < w N w_1 < w_2 < …… < w_N w1<w2<……<wN,以及它们出现的概率 p i p_i pi 。 如何将它们安放在一棵二叉查找树中使得总的期望访问时间最小化。
- 举个栗子 : 有如下一些单词和它们的访问概率
-

-

-
T ( N ) = ∑ i = 1 N p i ⋅ ( 1 + d i ) T(N)=\sum\limits_{i=1}^N p_i \cdot (1+d_i) T(N)=i=1∑Npi⋅(1+di)
-
最优二叉查找树的动态规划
- 最小代价的递归式
- C L e f t , R i g h t = min L e f t ≤ i ≤ R i g h t { p i + C L e f t − 1 + C i + 1 , R i g h t + ∑ j = L e f t i = 1 p j + ∑ j = i + 1 R i g h t p j } = min L e f t ≤ i ≤ R i g h t { C L e f t , i − 1 + C i + 1 , R i g h t + ∑ j = L e f t R i g h t p j } \begin {aligned} C_{Left,Right} &= \min\limits_{Left \leq i \leq Right} \left\{ \begin{matrix} p_i +C_{Left-1}+C_{i+1,Right} + \sum\limits_{j=Left}^{i=1}p_j + \sum\limits_{j=i+1}^{Right}p_j \end{matrix} \right\}\\ &= \min\limits_{Left \leq i \leq Right} \left\{ \begin{matrix} C_{Left,i-1}+C_{i+1,Right} + \sum\limits_{j=Left}^{Right}p_j \end{matrix} \right\} \end {aligned} CLeft,Right=Left≤i≤Rightmin{pi+CLeft−1+Ci+1,Right+j=Left∑i=1pj+j=i+1∑Rightpj}=Left≤i≤Rightmin{CLeft,i−1+Ci+1,Right+j=Left∑Rightpj}

最长公共子序列—LCS
-
Longest Common Subsequence
-
定义 : 给定两个序列 X X X和 Y Y Y, 当另一序列 Z Z Z既是 X X X的子序列又是 Y Y Y的子序列时, 称 Z Z Z是序列 X X X和 Y Y Y的公共子序列。
-
举个栗子 :
- X=< A, B, C, B, D, A, B >
- Y=< B, D, C, A, B, A >
- 则:LCS(X, Y)=<B, C, B, A>
- 或:
- X=< A, B, C, B, D, A, B >
- Y=< B, D, C, A, B, A >
- 则: LCS(X, Y)=<B, D, A, B>
-
定理 : LCS的最优子结构
- 设 X = < x 1 , x 2 , ⋯ , x m > X=<x_1,x_2,\cdots , x_m> X=<x1,x2,⋯,xm> 和 Y = < y 1 , y 2 , ⋯ , y n > Y = <y_1,y_2,\cdots,y_n> Y=<y1,y2,⋯,yn> 为两个序列,并设 Z = < z 1 , z 2 , ⋯ , z k > Z=<z_1, z_2, \cdots,z_k> Z=<z1,z2,⋯,zk> 为 X X X和 Y Y Y的任意一个LCS。
-
- 如果 x m = y n x_m=y_n xm=yn, 那么 z k = x m = y n z_k=x_m=y_n zk=xm=yn, 而且 Z k − 1 Z_{k-1} Zk−1是 X m − 1 X_{m-1} Xm−1和 Y n − 1 Y_{n-1} Yn−1的一个LCS。
- 如果 x m ≠ y n x_m \neq y_n xm=yn, 那么 z k ≠ x m z_k \neq x_m zk=xm, 则可推出 Z Z Z是 X m − 1 X_{m-1} Xm−1和 Y n Y_{n} Yn的一个LCS。
- 如果 x m ≠ y n x_m \neq y_n xm=yn, 那么 z k ≠ y n z_k \neq y_n zk=yn, 则可推出 Z Z Z是 X m X_{m} Xm和 Y n − 1 Y_{n-1} Yn−1的一个LCS。
-
LCS 的重叠子问题
- LCS的重叠子问题:为找出X和Y的一个LCS,可能需要找出 X X X和 Y n − 1 Y_{n-1} Yn−1的一个LCS,以及 X m − 1 X_{m-1} Xm−1和 Y Y Y的一个LCS。但这两个问题都包含找 X m − 1 X_{m-1} Xm−1和 Y n − 1 Y_{n-1} Yn−1的一个LCS的子子问题。原问题总共包含 O ( m n ) O(mn) O(mn)个不同的子问题,所以可以用DP自底向上来计算解。

-
LCS 的递归树
-
计算 LCS 长度的递归式
- 用 c [ i , j ] c[ i, j] c[i,j] 表示 X i X_i Xi 和 Y j Y_j Yj 的 LCS 的长度,则有 :
- c [ i , j ] = { 0 , i f i = 0 o r j = 0 c [ i − 1 , j − 1 ] + 1 , i f i , j > 0 a n d x i = y i m a x ( c [ i , j − 1 ] , c [ i − 1 , j ] ) , i f i , j > 0 a n d x i ≠ y i c[i,j]=\begin{cases}0, \qquad \ if \quad i=0 \ or \ j=0 \\c[i-1,j-1]+1, \quad if \quad i,j>0 \ and \ x_i=y_i \\ max(c[i,j-1],c[i-1,j]),\quad if \quad i,j>0 \ and \ x_i \neq y_i\end{cases} c[i,j]=⎩⎪⎨⎪⎧0, ifi=0 or j=0c[i−1,j−1]+1,ifi,j>0 and xi=yimax(c[i,j−1],c[i−1,j]),ifi,j>0 and xi=yi
-
计算LCS的长度
-
-
构造一个LCS
-
-
一个更通用的序列比对问题
- 20世纪70年代,分子生物学家Needleman和Wunsch提出了一个相似性的定义,用以描述两个序列的相似性。
- 问题定义:给定两个串 X X X, Y Y Y,假定 M M M是 X X X与 Y Y Y之间的一个比对,定义罚分规则如下:
- (1)存在一个参数 δ >0,用于定义空隙罚分。对于每个 X X X 或 Y Y Y 没在 M M M 中被匹配的位置 — 一个空隙,付出代价为 δ 。
- (2)对于字母表中的每对字符p和q,存在一个把p和q对准的错配代价 α p q α_{pq} αpq。于是,对每个 ( i , j ) ∈ M (i,j)\in M (i,j)∈M,我们把 x i x_i xi和 y j y_j yj对准支付 α x i y j α_{x_iy_j} αxiyj的错配代价。
- (3) M M M的代价是它的空隙和错配代价之和,我们要找一个最小代价的比对。
-
比对的定理
- 定理1:在一个最优比对M中,至少下述情况之一为真 :
-
- ( m , n ) ∈ M (m,n) \in M (m,n)∈M ;或者
- X X X的第 m m m个位置没被匹配;或者
- Y Y Y的第 n n n个位置没被匹配
-
- 定理1:在一个最优比对M中,至少下述情况之一为真 :
| m | e | a | n | - |
|---|---|---|---|---|
| n | - | a | m | e |
| -1 | -2 | -1 | -2 |
-
对比的递推式
- Recurrence:对于i≥1和j≥1,最小代价比对满足下面的递推式:
- O P T ( i , j ) = min { α x i , x j + O P T ( i − 1 , j − 1 ) δ + O P T ( i − 1 , j − 1 ) δ + O P T ( i , j − 1 ) } OPT(i,j) =\min \left\{ \begin{matrix} \alpha_{x_i,x_j} +OPT(i-1,j-1) \\ \delta + OPT(i-1,j-1) \\ \delta + OPT(i,j-1) \end{matrix} \right\} OPT(i,j)=min⎩⎨⎧αxi,xj+OPT(i−1,j−1)δ+OPT(i−1,j−1)δ+OPT(i,j−1)⎭⎬⎫
-
序列比对算法
-
比对示例
-
比对示例,最优比对结果如下。
-
δ=2
-
元对元,辅对辅=1
-
元音对辅音=3
-

-
m e a n - n - a m e -1 -2 -1 -2
-
图 中所有点对间的最短路径
- Floyd算法
- Floyd-Warshall 算法考虑最短路径上的中间节(intermediate),简单路径 p = < v 1 , v 2 , ⋯ , v l > p = <v_1, v_2, \cdots, v_l> p=<v1,v2,⋯,vl>上的中间节点是除 v 1 v_1 v1 和 v l v_l vl,以外的任意节点。
递归解
-
设 G 的节点为 V = { 1 , 2 , ⋯ , n } V = \{1, 2,\cdots, n\} V={1,2,⋯,n},对参数 k k k考虑节点集 { 1 , 2 , ⋯ , k } \{1, 2,\cdots, k\} {1,2,⋯,k} 。对任意一对节点 i , j ∈ V i, j \in V i,j∈V, 考虑从 i i i 到 j j j 且中间节点都属于集合 { 1 , 2 , ⋯ , k } \{1, 2,\cdots, k\} {1,2,⋯,k}的所有路径,设 p p p 是其中的最短路径。记为 d ( i , j , k ) d(i, j, k) d(i,j,k)有如下结论。
- 若 k 不是路径 p的中间节点,则p的所有中间节点属于集合 { 1 , 2 , ⋯ , k − 1 } \{1, 2,\cdots, k-1\} {1,2,⋯,k−1}。即 d ( i , j , k ) = d ( i , j , k − 1 ) d(i, j, k)= d(i, j, k-1) d(i,j,k)=d(i,j,k−1)
- 若 k k k 是 p p p 的中间节点,则如下图,可将 p p p分解为两条子路径,即 i → k → j i ~ \rightarrow k ~ \rightarrow j i →k →j 。 p 1 p_1 p1是从 i i i 到 k k k 中间节点属于集合 { 1 , 2 , ⋯ , k − 1 } \{1, 2,\cdots, k-1\} {1,2,⋯,k−1}的最短路径, p 2 p_2 p2 是从 k 到 j 中间节点属于 { 1 , 2 , ⋯ , k − 1 } \{1, 2,\cdots, k-1\} {1,2,⋯,k−1}的最短路径。
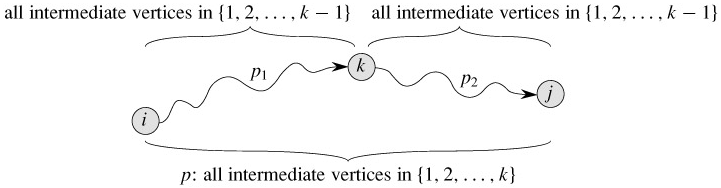
-
Floyd-Warshall 算法的递归解。 d ( i , j , k ) d(i, j, k) d(i,j,k)表示从 i i i 到 j j j 且中间节点都属于集合 { 1 , 2 , ⋯ , k } \{1, 2,\cdots, k\} {1,2,⋯,k}的所有路径中的最短路径的权值。
- d i j ( k ) = { w i j 若 k = 0 min ( d i j ( k − 1 ) , d i k ( k − 1 ) + d k j ( k − 1 ) ) 若 k ≥ 1 d^{(k)}_{ij} = \begin{cases}w_{ij} \quad 若k=0 \\ \min(d^{(k-1)}_{ij},d^{(k-1)}_{ik}+d^{(k-1)}_{kj}) \quad 若k\geq1 \end{cases} dij(k)={wij若k=0min(dij(k−1),dik(k−1)+dkj(k−1))若k≥1
Floyd算法示例
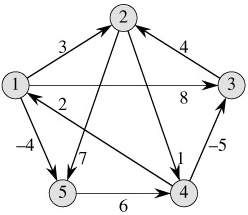


/* A[ ] contains the adjacency matrix with A[ i ][ i ] = 0 */
/* D[ ] contains the values of the shortest path */
/* N is the number of vertices */
/* A negative cycle exists iff D[ i ][ i ] < 0 */
void AllPairs( TwoDimArray A, TwoDimArray D, int N )
{ int i, j, k;
for ( i = 0; i < N; i++ ) /* Initialize D */
for( j = 0; j < N; j++ )
D[ i ][ j ] = A[ i ][ j ];
for( k = 0; k < N; k++ ) /* add one vertex k into the path */
for( i = 0; i < N; i++ )
for( j = 0; j < N; j++ )
if( D[ i ][ k ] + D[ k ][ j ] < D[ i ][ j ] )
/* Update shortest path */
D[ i ][ j ] = D[ i ][ k ] + D[ k ][ j ];
}
在某种意义上,如果你看出一个动态规划问题,那么你就看出了所有的问题。
随机算法
- 产生随机数的方法:线性同余法
- Lehmer(1951),
- X i + 1 = A X i m o d M X_i+1 = AX_i \mod M Xi+1=AXimodM
- Lehmer 建议 M = 2 31 − 1 M=2^{31-1} M=231−1(素数), A = 48271 A=48271 A=48271(能给出整周期)。
跳跃表
-
目标:以 O ( l o g N ) O(logN) O(logN)期望时间支持查找和插入的数据结构。
-

-
带有指向前 k k k个表元素的指针的链表,总的指针数加倍,但查找时间复杂度降为 O ( l o g N ) O(logN) O(logN)。但该结构的插入过于呆板。
-

-

-

-
采用随机方法实现的跳跃表。表中有1/2的一阶节点,1/4的二阶节点,…。按概率分布随机确定节点的阶数。任意 k k k 阶节点上的第 i i i 阶( k > = i k>=i k>=i)指针指向的下一个节点至少具有 i i i 阶。
-
跳跃表需要预估表中元素个数,以便确定节点阶的最大值。
-
跳跃表可以获得类似平衡查找树或伸展树的性能,但实现起来更简单。
素数测试问题
- 素数测试:确定一个数是否素数。
- 该问题不被认为是NP完全的,它的复杂性尚为未知。
模运算的几条性质
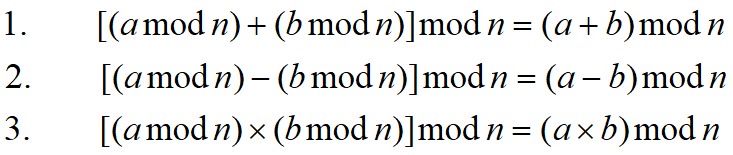

关于素数的几个定理
- 费马小定理 :如果 P P P是素数,且 0 < A < P 0<A<P 0<A<P,那么 A P − 1 ≡ 1 ( m o d P ) A^{P-1} ≡ 1 (\mod P) AP−1≡1(modP)。
- 因此,对于整数 N N N,若 2 N − 1 ≠ 1 ( m o d N ) 2N-1 \neq 1 (\mod N) 2N−1=1(modN),那么可以肯定 N N N不是素数。
- 平方探测定理 :如果 P P P是素数且 0 < X < P 0<X<P 0<X<P,那么 X 2 ≡ 1 ( m o d P ) X^2 ≡ 1 (\mod P) X2≡1(modP)仅有的两个解为 X = 1 X=1 X=1, P − 1 P-1 P−1。
费马定理证明

平方探测定理的证明
- 平方探测定理 :如果P是素数且
0
<
X
<
P
0<X<P
0<X<P,那么
X
2
≡
1
(
m
o
d
P
)
X^2 ≡ 1 (\mod P)
X2≡1(modP)仅有的两个解为
X
=
1
X=1
X=1,
P
−
1
P-1
P−1。
- 证明: X 2 ≡ 1 ( m o d P ) X^2≡1 (\mod P) X2≡1(modP)意味着 X 2 − 1 ≡ 0 ( m o d P ) X^2-1 ≡ 0 (\mod P) X2−1≡0(modP)。即 ( X − 1 ) ( X + 1 ) ≡ 0 ( m o d P ) (X-1)(X+1)≡0 (\mod P) (X−1)(X+1)≡0(modP)。由于P是素数, 0 < X < P 0<X<P 0<X<P,因此P必然是或者整除 ( X − 1 ) (X-1) (X−1),或者整除 ( X + 1 ) (X+1) (X+1),所以定理成立。
使用随机方法测试素数的思路
-
(1)利用费马小定理,选用不同的 A ( 0 < A < P ) A( 0<A<P ) A(0<A<P),对待测数P执行 A P − 1 m o d P A^{P-1} \mod P AP−1modP,若结果≠1,则可以肯定 P P P是不是素数;若结果=1,则换别的 A A A测试。若用了很多不同的 A A A,结果都=1,则P是素数的可能性非常大。
-
(2)利用平方探测定理,若 X 2 ≡ 1 ( m o d P ) X^2 ≡ 1 (\mod P) X2≡1(modP)仅有的两个解不是 X = 1 , P − 1 X=1,P-1 X=1,P−1,则 P P P一定不是素数;反之,采用不同的 X X X继续测。
-
若函数Witness返回任何不是1的数,那么就已经证明了N不是素数(但证明是非构造性的)。也已证明,对于任何 N N N,至多有A的 ( N − 9 ) / 4 (N-9)/4 (N−9)/4个值会使该算法得出错误的结论。因此,若A是随机选取的,而算法的结论是“N是素数”,那么该算法有75%的概率是正确的。
-
HugeInt Witness( HugeInt A, HugeInt i, HugeInt N ) { HugeInt X, Y; if( i == 0 ) return 1; X = Witness( A, i / 2, N ); if( X == 0 ) /* If N is recursively composite, stop */ return 0; /* N is not prime if we find a non-trivial root of 1 */ Y = ( X * X ) % N; if( Y == 1 && X != 1 && X != N - 1 ) return 0; if( i % 2 != 0 ) Y = ( A * Y ) % N; return Y; } /* IsPrime: Test if N >= 3 is prime using one value of A */ /* Repeat this procedure as many times as needed for */ /* desired error rate */ int IsPrime( HugeInt N ) { return Witness( RandInt( 2, N - 2 ), N - 1, N ) == 1; }
回溯算法
- 许多情况下,回溯相当于穷举搜索的巧妙实现,但性能一般不理想。
收费公路重建问题
-
收费公路重建问题 :给定X轴上的 N N N 个点,其坐标满足 x 1 < x 2 < ⋯ < x N x_1 < x_2 < \cdots < x_N x1<x2<⋯<xN。假设 x 1 = 0 x_1 = 0 x1=0。 每一个点对间有一个距离,共计 N ( N – 1 ) / 2 N ( N – 1 ) / 2 N(N–1)/2 个点对间的距离。给定这 N ( N – 1 ) / 2 N ( N – 1 ) / 2 N(N–1)/2 个距离。请根据这些距离数据重建这 N N N个点序列。
-

-

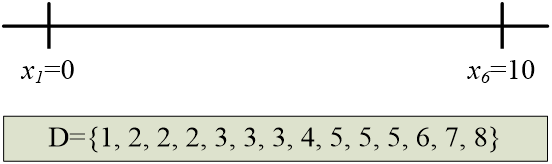
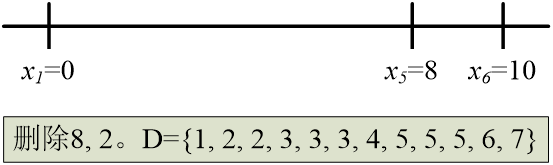
- 首先确定 x 1 = 0 x_1=0 x1=0 和 x 6 = 10 x_6=10 x6=10。
- 接下来可以尝试 x 5 = 8 x_5=8 x5=8。

-
再尝试x4=7。
-
剩下的距离中,最大为6。因此,要么 x 3 = 6 x_3=6 x3=6,要么 x 2 = 4 x_2=4 x2=4。若 x 3 = 6 x_3=6 x3=6,则 x 4 − x 3 = 1 x_4-x_3=1 x4−x3=1,而1已不在集合中;若 x 2 = 4 x_2=4 x2=4, x 2 − x 0 = 4 x_2-x_0=4 x2−x0=4, x 5 − x 2 = 4 x_5-x_2=4 x5−x2=4,这都是不可能的。所以需要回溯。
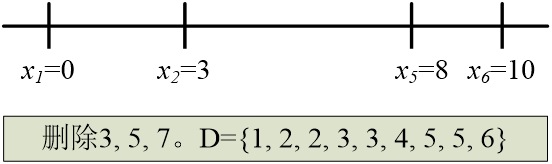
- 回溯,撤消 x 4 = 7 x_4=7 x4=7,尝试 x 2 = 3 x_2=3 x2=3。
- 接下来需要在 x 4 = 6 x_4=6 x4=6和 x 3 = 4 x_3=4 x3=4之间做出选择。而 x 3 = 4 x_3=4 x3=4是错的,因为 x 3 − x 1 = 4 x_3-x_1=4 x3−x1=4, x 5 − x 3 = 4 x_5-x_3=4 x5−x3=4。
- 所以选择 x 4 = 6 x_4=6 x4=6。

- 最后剩下唯一的选择是 x 3 = 5 x_3=5 x3=5,而这是可行的。
皇后问题
- 问题描述:在8×8的国际象棋盘上放8个皇后,使得任意两个皇后都不能相互吃掉。规则:皇后能吃掉同一行、同一列、同一对角线的任意棋子。

- 回溯法求解
public boolean positionIJOk(int[][] queens, int i, int j) {
//检测在queens数组中位置(i,j)是否合法
int m,n;
boolean ok=true;
for (m=i-1;m>=0;m--) //垂直上方
if (queens[m][j]==1) ok=false;
for (m=i-1,n=j-1;m>=0 && n>=0;m--,n--) //左上方
if (queens[m][n]==1) ok=false;
for (m=i-1,n=j+1;m>=0 && n<8;m--,n++) //右上方
if (queens[m][n]==1) ok=false;
return ok;
}
int[][] queens=new int[8][8];
for (i=0;i<8;i++)
for (j=0;j<8;j++)
queens[i][j]=0;
int[] position=new int[8];
for (i=0;i<8;i++) position[i]=-1;
i=0;
while (i<=7 && i>=0) {
for (j=position[i]+1;j<=7;j++) {
//测试位置(i,j)是否合适
if (positionIJOk(queens,i,j)) {
queens[i][j]=1;//放置皇后
position[i]=j;//记下皇后在当前行的位置
i=i+1;
j=20;//强制跳出循环
}
}
if (j==8) {//在本行没找到合适位置
position[i]=-1;//回溯前将position[i]复原
i=i-1;//退回上一行,回溯
if (i>=0) queens[i][position[i]]=0;//i<0为结束条件
}
}
- 递归算法
private int[][] queens=new int[8][8];
public QueensRecursion() {
//构造函数,对queens初始化
int i,j;
for (i=0;i<8;i++)
for (j=0;j<8;j++)
queens[i][j]=0;
}
public boolean queensRecursion(int i) {//求解八皇后问题,输出一个可行解
int j;
if (i==8) {
printQueens();//输出一个解
return true
} else {
for (j=0;j<8;j++) {
if (positionIJOk(i,j)) {
queens[i][j]=1;
if (queensRecursion(i+1)) {
return true;//当前位置合法且下一阶问题为true,则返回true
} else {
queens[i][j]=0;//下一阶问题为false,则复原
}
}
}
return false;
}
}
- 递归函数的调用方法
public static void main(String[] args) {
QueensRecursion eq1;
boolean bl;
//测试queensRecursion
System.out.println("Test queensRecursion...");
eq1=new QueensRecursion();
bl=eq1.queensRecursion(0);
}
博弈
-
三连棋
-

-
三连棋的分析
- 终端位置:通过考察盘面能确定这局棋输赢的位置称为终端位置。
- 极小极大策略:如果一个位置不是终端位置,那么该位置的值通过递归地假设双方最优棋步而确定。该策略叫极小极大策略,因为下棋的一方(人)试图使这个位置的值极小,而另一方(计算机)却要使它的值极大。
- 位置P的后继位置:即从P走一步后能到达的任何位置Ps。若在某个位置P,计算机要走棋,则需要递归地计算所有后继位置的值,然后选定具有最大值的一个后继位置。
- 为了得到Ps的值,要递归地计算出Ps的所有后继位置,然后选择其中最小的值。
-
通过置换表降低搜索层次












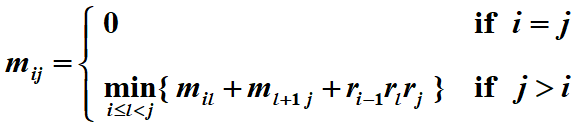







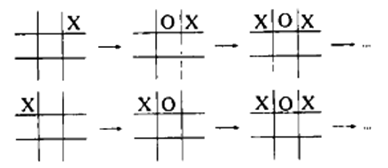














 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








