高等数学Mathematica实验题——绘制函数图形（y=1/1+x^2, y=e^(-x)sinx等）

“在数学中，函数 f 的图形（或图象）指的是所有有序对（x, f(x)）组成的集合。具体而言，如果x为实数，则函数图形在平面直角坐标系上呈现为一条曲线。如果函数自变量为两个实数组成的有序对（x, y)，则图形就是空间上的点（x, y, f(x, y)）组成的集合，呈现为曲面。”

如果不借助计算机，手绘函数图形需经过三步曲：取点、描点、连线（注意画出特殊点（间断点、顶点、尖点、拐点等）。要准确画出函数图形，需掌握函数的几个重要的性质：单调性、最值、周期性、奇偶性、对称性等，以及几个基本变换（平移、对称、伸缩）。

所以，必须感谢Mathematica这样的数学软件，有了它，画个函数图形仅需一行命令即可。

言归正传，这道实验题并不难（不是那种花几个小时还解不出来的题目）。

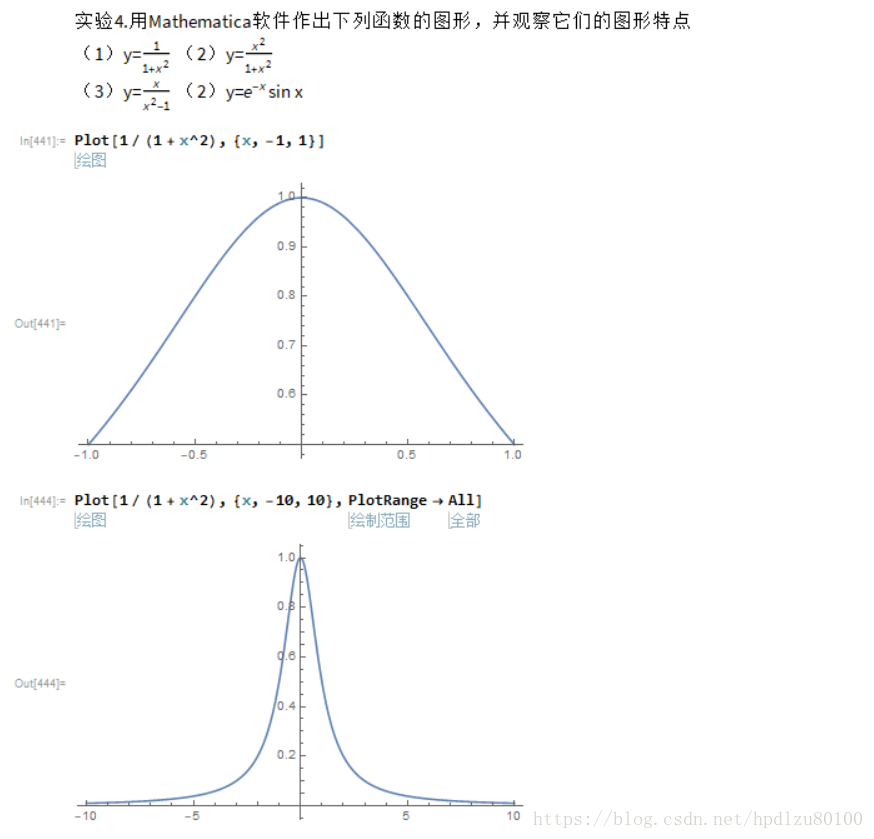
彩蛋：需要注意一点，要灵活使用“PlotRange -> All”这一选项（对函数图形具体呈现影响很大！）。如果你觉得画出的函数图形有点奇怪，可试着在命令中加入该选项；如果觉得函数比例失调，可试着移除该选项。毕竟，计算机是帮我们干活的，干的好不好，还需主人说了算。