1 问题的提出
由于在现实生活中,我们的观察尺度有限,我们的样本(输入)很可能没有办法包含所有可能的情况,那么我们怎么去处理先前看不见的事件呢?
举个例子,莎士比亚使用了30000个双连词(bigram),然而我们总共有V^2=8.44亿个可能的双连词,所以,99.96%的可能的双连词都没有出现过,那是不是意味着,任何句子包含有其中某一种双连词的概率就为0呢?同样的问题有很多,当我们面对的升起问题时,我们联系观察了20天,即我们手里有20个样本,这20个样本都显示,明天太阳会升起,但是是不是意味着“明天太阳会升起”这个事件发生的概率是100%呢?
当然,我们不能否认,在我们设置的所有事件里,某些事件发生的概率真的是0,也就意味着它们真的不会发生,但是这种情况往往比我们认为的要少。在另一方面,这些我们从有限的样本中推理出出不会发生的事件很可能只是一个小概率事件,这些事件发生的可能性会比样本的估计值要大。那么,我们怎么去评估这些模型呢?
首先,我们会定义一个评估度量标准(evaluation metric),通常被称为得分函数(scoring function),我们想去测量模型的预言与真实情况的相似度。
其次,我们会用可见的训练集进行训练,也许我们会在留存数据上进行协调(tune),为了对不可见的数据进行仿真。
最后,我们会在不可见的测试集上进行测试,不过通常跟训练集是一个集合。测试数据必须要从训练集和留存数据中解体(disjoint),通过他们的得分来比较模型。
在文本分类中,有一种效应为Zipf’s Law,有兴趣的朋友可以去了解一下长尾现象(long tail phenomenon)。这个效应是这样描述的:
高频率发生的事件是少量的,低频率发生的事件是大量的。你可以迅速收集高频率事件的统计数据,却需要很长时间去收集低频率事件的合适的统计数据。结果就造成了我们的估计很自然地变得很稀疏,大量我们想要评估的数据甚至都没有计数。解决的办法就是要对看不见的n-元模型进行似然估计。处理的办法通常有两种:
第一种:使用一种完全不同的评估技术
其中包括拉普拉斯平滑(Add-1(Laplace) Smoothing), Good-TuringDiscounting,核心思想是取代MLE估计
第二种:将一个复杂的模型和一个更简单的模型联合使用。
其中包括线性插值(Linear Interpolation),修改Knesser-Ney平滑(Modified Knesser-Ney smoothing),核心思想是使用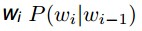
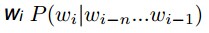
平滑算法就像是罗宾汉(Robin Hood)一样,劫富济贫:
2.拉普拉斯平滑(Laplace smoothing)
明天太阳会升起吗?
拉普拉斯平滑是拉普拉斯在研究太阳升起问题时提出的。
其中,第n+1天,我们观察到之前太阳升起了s次,则今天太阳升起的概率为
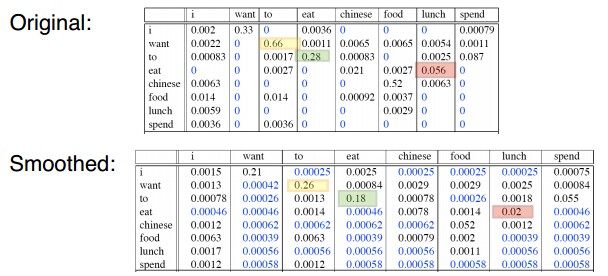
拉普拉斯平滑既然被称作加一平滑,自然是在每一个计数上加一。我们以一个词典为例,我们从一个大小为V的词典里,独立得取出N个词,我们有一元概率:
每个计数上加一:
结果为:
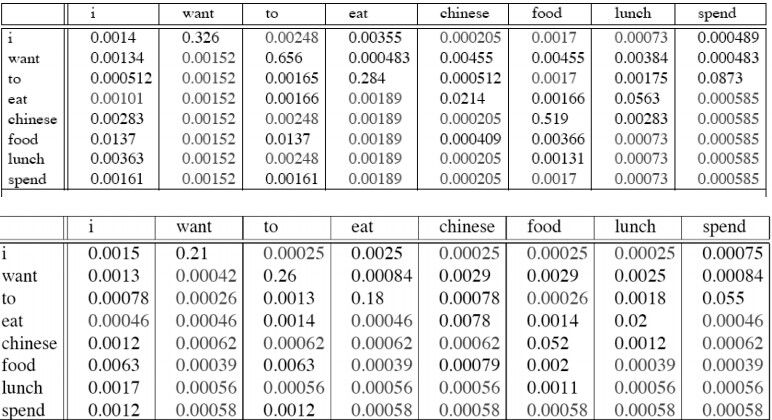
二元概率:
这里有一个问题,就是加一算法从可见事件到不可见事件移动的概率块太多了。
我们重组一下伪计数:
对一元模型:
对二元模型:
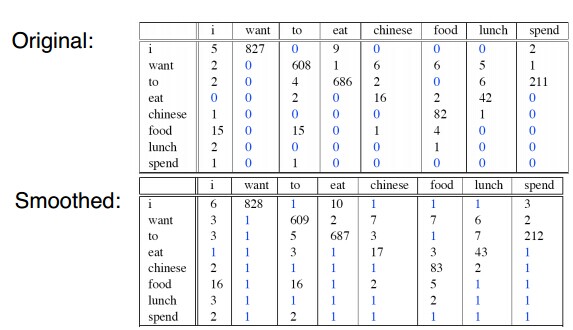
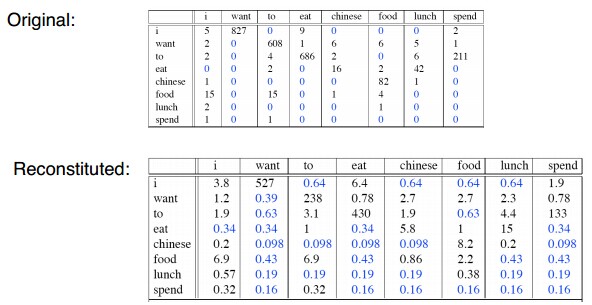
我们可以对比重组之后的二元计数:
所以我们可以总结一下拉普拉斯平滑:
优点:简单,便于实现
缺点:转移太多的概率
回到之前的莎士比亚问题上,V=30000个词,’the’出现25545次,’the’的概率为
既然拉普拉斯平滑在N元模型上的效果并不好,那么我们就会有更好的平滑算法
3. Good-Turing smoothing
现在假设你正在钓鱼,现在湖里有八种鱼:carp, perch, whitefish, trout, salmon, eel,catfish, bass,你现在已经钓到了10 carp, 3 perch, 2 whitefish, 1 trout, 1salmon, 1 eel = 18 fish。所以,下次钓鱼钓到没钓过的种类(catfish or bass)的概率是多少呢?
下次钓鱼又钓到trout的概率是多少呢?我们一会来回答这个问题。
现在定义: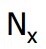
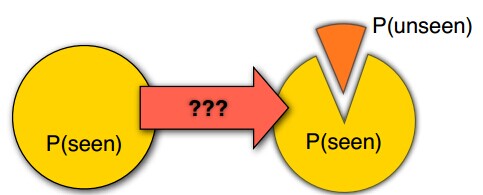
所以,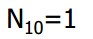
因此,去评估一个没见过的种类:
其他的评估都要向下调整,来适应未出现的概率:
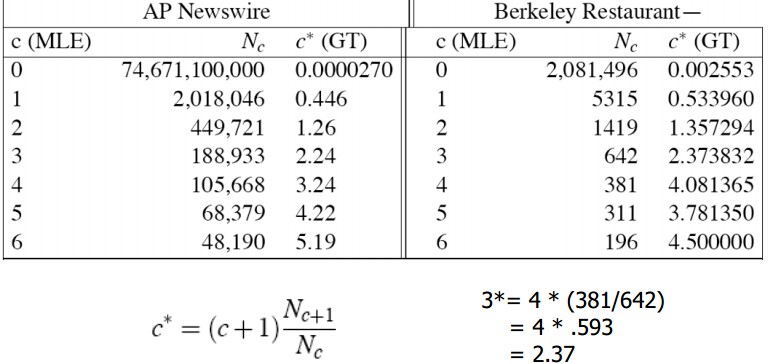
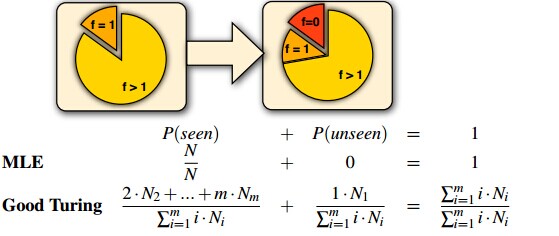
二元频率的频率于GT重组估计:
GT平滑的二元概率:
我们再重新回顾一下Good-Turing smoothing的思想:使用仅发生一次的事件的总频率,去估计可见事件到不可见事件的转移概率。
其中,Nc代表发生c次的时间的个数。
将发生n次的事件的概率块分配给发生n-1次的事件。
Nn发生了n次,总频率为n⋅Nn
所以,发生n-1次的事件的概率就变成:
Good-Turing代替原始的Cn-1,变成了新的C*n-1:
事件w发生n-1次的极大似然估计为:
事件w发生n-1次的Good-Turing估计为:
Good-Turing无法解决的问题有:
1. 无法处理更频繁的事件
2. 不对每一个n都观察事件
Good-Turing的变体:Simple Good-Turing
将Nn替换成一个适应函数f(n):
4.线性插值(Linear Interpolation)
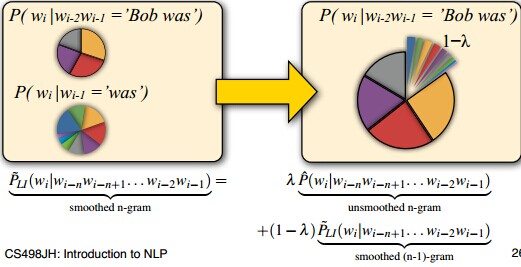
假如我们没有看到”Bob was reading”,我们看到了“__ was reading”,我们将会估计P(reading |’Bob was’) =0而不是 P(reading | ‘was’) > 0。
所以我们尝试着使用n-1元概率去估计n-元概率:
我们从来不会看到“Bob was reading”,但是我们可能会看到“__ was reading”,或者更直接的看到“__ reading”。
λ的上下文条件:
但是现在面临一个问题:怎样设置λ。我们有两种思想:
A:留存估计
将数据分成训练数据和留存数据,根据训练数据评估模型,利用留存数据(或者一些优化技术)去寻找使模型表现更好的λ(有点像k-折叠交叉验证)。当然,λ也可以取决于Wi-n...Wi-1
B:λ是Wi-n...Wi-1频率的函数
其他的平滑算法还包括绝对折扣(Absolute discounting),Kneser-Ney smoothing,和bayesian prior Smoothing.其中bayesian prior Smoothing为:








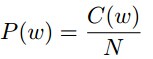


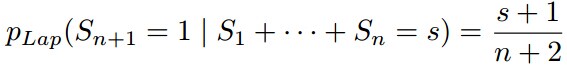
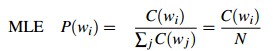
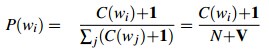
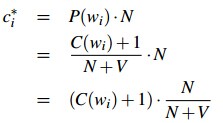
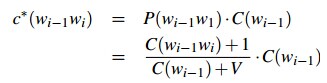
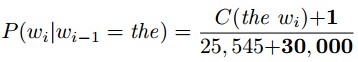
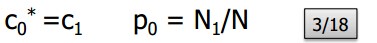

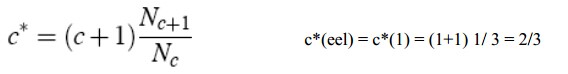

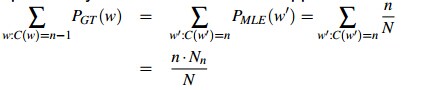
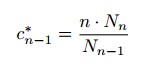
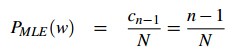
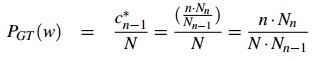
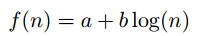
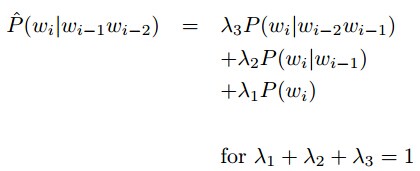
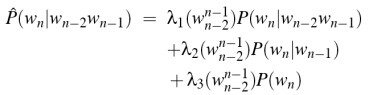
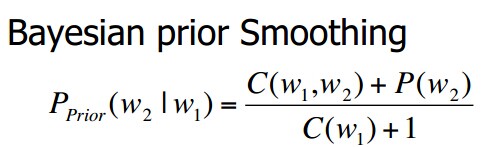














 7813
7813

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








