[kuangbin]莫比乌斯反演——入门

最新推荐文章于 2019-01-04 13:47:00 发布

Sega_hsj

最新推荐文章于 2019-01-04 13:47:00 发布

阅读量309

点赞数

分类专栏：莫比乌斯反演文章标签：莫比乌斯反演

本文链接：https://blog.csdn.net/hsj970319/article/details/77138513

版权

莫比乌斯反演专栏收录该内容

0 篇文章 0 订阅

订阅专栏

说是入门吧，其实写了那几题之后还是不会(

莫比乌斯反演是数论中比较重要的部分了，公式到处都有，重点就是怎么求出μ函数和如何反演，目前做到的题目好像都是利用的变形后的公式，就是：
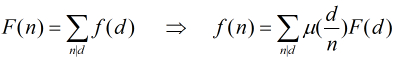
这里写图片描述
变形前统计的是能整出n的那些，变形后统计的是n的倍数的那些。

专题里的所有题目都是跟gcd有关，让人有点怀疑莫比乌斯只能处理这类问题吗，莫比乌斯反演主要就是你要求f(n)但是求这个的复杂度太高，然而F(n)可以直接得出，然后就利用反演就能比较方便的得出f(n)。
就如gcd来说，你要求平面上gcd(x,y)=1的点对，暴力枚举的话就n^2*gcd的复杂度咯。但是对于gcd(x,y)=i的倍数的点对数量，只要x是i的倍数，y是i的倍数的所有点对就都满足了，数量也就是（x/i）*（y/i）,然后我们利用反演就能在较低的复杂度求出来了。
由于在枚举i的时候会出现连续的i，(x/i)和(y/i)的值都是不变的，所以可以利用这个加速计算

A - Visible Lattice Points——SPOJ - VLATTICE

三维空间内求gcd(x,y,z)=1的点的数量，要特殊处理一个坐标为0和两个坐标为0的点。

#include<bits/stdc++.h>
using namespace std;
#define MEM(a,b) memset(a,b,sizeof(a));
typedef long long ll;
const int maxn=1000005;
const int maxq=300005;
const int maxm=3000005;
const int inf=0x3f3f3f3f;
ll n,m,q;
int mu[maxn];
bool vis[maxn];
int prime[maxn];
int tot;
void get_mu(){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;prime[j]*i<maxn&&j<tot;j++){
            vis[prime[j]*i]=1;
            if(i%prime[j]==0){mu[prime[j]*i]=0;break;}
            mu[prime[j]*i]=-mu[i];
        }
    }
}

int main()
{
  get_mu();
  int t;
  scanf("%d",&t);
  while(t--){
    scanf("%lld",&n);
    ll ans=3;
    for(int i=1;i<=n;i++){
        ans=ans+mu[i]*(n/i)*(n/i)*(n/i);
    }
    for(int i=1;i<=n;i++){
        ans=ans+mu[i]*(n/i)*(n/i)*3;
    }
    printf("%lld\n",ans);
  }

   return 0;
}

B - GCD——HDU - 1695

求平面上x in a…b, y in c…d that GCD(x, y) = k
问题转化成x in a/k…b/k, y in c/k…d/k that GCD(x, y) = 1
重点是要去重，因为(3，5)和(5，3)是算重复的，统计F(i)时变成
ll lef=ll(b)/i;
ll rig=ll(d/i);
ll mm=min(lef,rig);
F(i)=(lef*rig-mm*(mm-1)/2);

#include<bits/stdc++.h>
using namespace std;
#define MEM(a,b) memset(a,b,sizeof(a));
typedef long long ll;
const int maxn=110005;
const int maxq=300005;
const int maxm=3000005;
const int inf=0x3f3f3f3f;
ll a,b,c,d,k;
int mu[maxn];
bool vis[maxn];
int prime[maxn];
int tot;
void get_mu(){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;prime[j]*i<maxn&&j<tot;j++){
            vis[prime[j]*i]=1;
            if(i%prime[j]==0){mu[prime[j]*i]=0;break;}
            mu[prime[j]*i]=-mu[i];
        }
    }
}

int main()
{
  get_mu();
  int t;
  int cas=0;
  scanf("%d",&t);
  while(t--){
    cas++;
    scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
    printf("Case %d: ",cas);
    if(k==0){printf("0\n");continue;}
    b/=k;
    d/=k;
    if(b==0||d==0)printf("0\n");
    else {
        ll ans=0;
        for(int i=1;i<=min(b,d);i++){
            ll lef=ll(b)/i;
            ll rig=ll(d/i);
            ll mm=min(lef,rig);
            ans+=mu[i]*(lef*rig-mm*(mm-1)/2);
        }
        printf("%lld\n",ans);
    }
    }
   return 0;
}

C - Mophues——HDU - 4746

还不是很懂/。。。。

//其实根本就还不会这题
#include<bits/stdc++.h>
using namespace std;
#define MEM(a,b) memset(a,b,sizeof(a));
typedef long long ll;
const int maxn=500005;
const int maxm=3000005;
const int inf=0x3f3f3f3f;
int n,m,p;
int mu[maxn];
int cnt[maxn];
bool vis[maxn];
int prime[maxn];
int f[maxn][20];
int tot;

void init(){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
            cnt[i]=1;
        }
        for(int j=0;j<tot&&prime[j]*i<maxn;j++){
            vis[prime[j]*i]=1;
            cnt[i*prime[j]]=cnt[i]+1;
            if(i%prime[j]==0){mu[prime[j]*i]=0;break;}
            mu[prime[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<maxn;i++){
        for(int j=i;j<maxn;j+=i){
            f[j][cnt[i]]+=mu[j/i];
        }
    }
    for(int i=1;i<maxn;i++){
        for(int j=1;j<20;j++){
            f[i][j]+=f[i][j-1];
        }
    }
    for(int i=1;i<maxn;i++){
        for(int j=0;j<20;j++){
            f[i][j]+=f[i-1][j];
        }
    }
}


int main(){
   init();
   int T;
   scanf("%d",&T);
    while(T--){
   scanf("%d%d%d",&n,&m,&p);
   if(p>18){
    printf("%lld\n",ll(n)*m);
    continue;
   }
    ll ans=0;
    int last;
    for(int i=1;i<min(n,m);i=last+1){
        last=min(n/(n/i),m/(m/i));
        ans+=ll(f[last][p]-f[i-1][p])*(n/i)*(m/i);
    }
    printf("%lld\n",ans);
    }
   return 0;
}

E - Gcd——HYSBZ - 2818

统计gcd为质数的点的数量
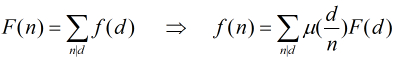
这里写图片描述
根据公式右边，f(prime[i])=sigmaμ(d/prime[i])F(d)
这里的d就是质数的倍数，开一个数组存每一个F(d)对应的sigma μ(d/prime)然后求和统计，我觉得直接枚举质数来做也行？

#include<bits/stdc++.h>
using namespace std;
#define MEM(a,b) memset(a,b,sizeof(a));
typedef long long ll;
const int maxn=10000105;
const int maxm=3000005;
const int inf=0x3f3f3f3f;
int n;
bool vis[maxn];
int prime[maxn];
int mu[maxn];
int sum[maxn];
int tot;
void init(int maxn){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;prime[j]*i<maxn&&j<tot;j++){
            vis[prime[j]*i]=1;
            if(i%prime[j]==0){mu[prime[j]*i]=0;break;}
            mu[prime[j]*i]=-mu[i];
        }
    }
}

int main(){
   scanf("%d",&n);
   init(n+4);
   ll ans=0;
   for(int i=0;i<tot;i++){
        for(ll j=prime[i];j<=n;j+=prime[i]){
            sum[j]+=mu[j/prime[i]];
        }
   }
   for(int i=1;i<=n;i++){
        ans+=sum[i]*ll(n/i)*(n/i);
   }
   printf("%lld\n",ans);
   return 0;
}

F - 能量采集——HYSBZ - 2005

对于gcd为i的点，能量损失为gcd(x,y)*2-1,其余的跟之前的问题都差不多，使用了加速计算。

#include<bits/stdc++.h>
using namespace std;
#define MEM(a,b) memset(a,b,sizeof(a));
typedef long long ll;
const int maxn=100005;
const int maxm=3000005;
const int inf=0x3f3f3f3f;
int n,m;
int mu[maxn];
bool vis[maxn];
int prime[maxn];
int sum[maxn];
int tot;

void init(int maxn){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<tot&&prime[j]*i<maxn;j++){
            vis[prime[j]*i]=1;
            if(i%prime[j]==0){mu[prime[j]*i]=0;break;}
            mu[prime[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<maxn;i++){
        sum[i]=sum[i-1]+mu[i];
    }
}

ll cal(int x,int y,int k){
    ll ans=0;
    int last;
    x/=k,y/=k;
    for(int i=1;i<=min(x,y);i=last+1){
        last=min(x/(x/i),y/(y/i));//i到last这段x/i and y/i都相等
        ans+=ll(sum[last]-sum[i-1])*(x/i)*(y/i);
    }
    return ans;
}

int main(){
    scanf("%d%d",&n,&m);
    init(max(n,m)+1);
    ll ans=0;
    for(int i=1;i<=min(n,m);i++){
        ans+=(2*i-1)*cal(n,m,i);
    }
    printf("%lld\n",ans);
   return 0;
}

G - Problem b——HYSBZ - 2301

也是跟之前的题目差不多，就是统计区间换了，加加减减一下就行了。

#include<bits/stdc++.h>
using namespace std;
#define MEM(a,b) memset(a,b,sizeof(a));
typedef long long ll;
const int maxn=50005;
const int maxm=3000005;
const int inf=0x3f3f3f3f;
int a,b,c,d,k;
int mu[maxn];
bool vis[maxn];
int prime[maxn];
int sum[maxn];
int tot;

void init(){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<tot&&prime[j]*i<maxn;j++){
            vis[prime[j]*i]=1;
            if(i%prime[j]==0){mu[prime[j]*i]=0;break;}
            mu[prime[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<maxn;i++){
        sum[i]=sum[i-1]+mu[i];
    }
}

ll cal(int x,int y,int k){
    ll ans=0;
    int last;
    x/=k,y/=k;
    for(int i=1;i<=min(x,y);i=last+1){
        last=min(x/(x/i),y/(y/i));//i到last这段x/i and y/i都相等
        ans+=ll(sum[last]-sum[i-1])*(x/i)*(y/i);
    }
    return ans;
}

int main(){
   init();
   int T;
   scanf("%d",&T);
    while(T--){
   scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
    ll ans=0;
    a--,c--;
    ans+=cal(b,d,k);
    if(c)
    ans-=cal(b,c,k);
    if(d)
    ans-=cal(a,d,k);
    if(c&&d)
    ans+=cal(a,c,k);
    printf("%lld\n",ans);
    }
   return 0;
}