无线传感器网络自适应混合压缩

无线传感器网络中的自适应混合压缩

阿扎德·阿里、阿卜杜勒马吉德·赫利尔、尼拉杰·苏里和穆罕默德雷扎·马赫穆迪马内什，达姆施塔特工业大学

无线传感器网络（WSNs）通常被部署用于采样所需环境属性，并将获取的样本传送到称为汇聚节点的中心站， 以供应用程序按需处理。许多应用要求高粒度和高数据精度，从而导致大量数据产生。然而，传感器节点是电池 供电的，频繁发送大量请求的数据会迅速耗尽其能量。幸运的是，环境属性（例如温度、压力）通常表现出空间 和时间相关性。此外，诸如科学分析和仿真等大量应用对传感器数据采集具有较高的延迟容忍度。因此，我们在 利用传感器读数的时空相关性的同时，结合可能的数据传输延迟容忍度，以最小化需要传输到汇聚节点的数据量。 为此，我们提出一种完全去中心化的自适应混合压缩方案，该方案充分利用了空间和时间上的数据冗余，并融合 时间压缩与空间压缩，以在保证精度的前提下实现最大程度的数据压缩。我们提出了两项主要贡献：（i）一种自 适应建模技术，通过利用数据采集延迟，在资源受限的传感器节点上实现高效且最大化的时间压缩；（ii）一种 新颖的基于模型的分层聚类技术，可实现最大化的空间压缩，从而构成一种混合压缩方案。与现有的时空压缩方 法相比，我们的方法是完全去中心化的，所提出的聚类方案基于传感器数据模型而非瞬时传感器数据值，这使得 在较长时间段内可将具有相似模型的邻近节点合并为较大的簇，而不是局限于特定的时间实例。对计算和消息开 销的分析、理论可压缩性的分析以及基于真实世界数据的仿真结果表明，所提方案能够在不牺牲采集数据准确性 的前提下，显著降低通信/能量消耗。

分类与主题描述：C.2.2[Network Protocols]：应用（SMTP、FTP等）；C.2.4[Distributed Systems]：分布式 应用；E.4[Coding and Information Theory(H.1.1)]：数据压缩与缩减；I.6.8[Types of Simulation]：分布式

通用术语：设计，算法，性能 Addi关键词和短语：基于模型的聚类，时空压缩，延迟容忍 t netw网络，数据分析

ACM参考格式： 阿扎德·阿里、阿卜杜勒马吉德·赫利尔、尼拉杰·苏里和穆罕默德雷扎·马赫穆迪马内什。2015年。无线传感器网络的自 适应混合压缩。ACM传感器网络汇刊11,4,文章53(2015年5月),36页。DOI:http://dx.doi.org/10.1145/2754932

1. 问题与方法

在无线传感器网络（WSN）部署中，电池供电的传感器节点通常分布在感兴趣区域，用于 各种应用，包括无人值守的环境监测和监控功能。传感器节点定期更新一个被称为汇聚节点的中心站，以传输采样的环境数据，供后续处理和分析。从节点到汇聚节 点的（多跳）数据传输需要交换多个消息，从而消耗参与传输的传感器节点的电池电量，并缩 短剩余网络寿命。因此，如何在持续收集数据的同时延长网络寿命，是一个具有挑战性的问题。

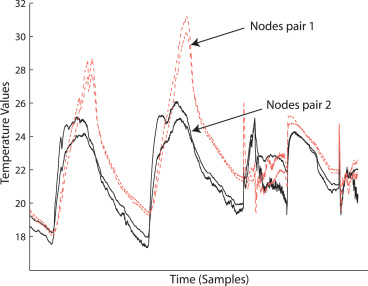
幸运的是，由于以下两个原因，无线传感器网络（WSN）天然地产生了高度冗余的空 间样本：（a）为实现连通性和容错性而进行的冗余传感器节点部署；（b）环境属性在较 大空间区域上的相关值。这一点也得到了我们对现有真实世界数据[Madden 2003],的观 察结果的支持，在该数据中我们注意到，在给定物理邻域内的大量节点中，其趋势/模式是 相似的。图1描绘了来自Madden[2003], 的两对节点在四天时间内的传感器读数。每对 中的节点互为单跳邻居，且这两对节点之间相隔多个跳距。采样属性值还表现出时间相关 性[Tulone和Madden 2006]，可通过构建数据模型并报告模型参数而非原始样本值来 利用这种相关性。

问题界定。 需要连续数据采集的应用通常将数据用于两种主要用途：（a）实时决策， 例如监控；或（b）离线/延迟容忍处理，例如建模、分析[Tolle等人2005], 和推断[Ali 等人 2009]。我们当前工作的重点是延迟容忍数据采集。许多用于科学监测的无线传感器 网络[Werner‐Allen等人2005；Akyildiz等人2005；Tolle等人 2005] 持续采集数据 用于建模、分析和仿真，通常可容忍一定程度的数据采集延迟。因此，对于此类应用而言， 实时数据采集并不优先于数据的质量和数量。这种将数据上报至汇聚节点的延迟容忍性为 数据采集带来了根本性的设计灵活性，可显著提高无线传感器网络的能量效率。我们提出 一种自适应混合压缩方案，该方案明确利用数据采集中的延迟容忍性，在时间和空间上压 缩数据，相比要求频繁更新并与汇聚节点同步的实时方案，具有显著优势。

压缩努力。 已经提出了多种方法，如聚合、时间压缩[Jindal和Psounis2006；Zhao等 人 2002],以及空间压缩[Deshpande等人2004；Zhang等人 2006]，以减少需传输至汇聚 节点的数据量。然而，仅有少数复合时空方法存在，例如Gedik等人[2007],、Tulone和 Madden[2006],、Wang等人[2012],、Yoon和Shahabi[2007],以及Ali等人[2011],。 这些方法利用了数据中的空间和时间相关性，从而实现更高的数据流量减少。

然而，现有的方法存在以下问题：(a)部分为集中式，限制了本地决策能力，从而影响适应 性；(b)针对特定的属性动态进行设计，缺乏或仅有有限的自适应能力；或(c)在利用空间 或时间相关性方面范围有限，降低了压缩性。Ali等人[2011] 是唯一在时空数据压缩中考 虑延迟容忍的工作。然而，由于采用静态模型且数据压缩的范围有限，其应用受到限制。

我们所提出方法的基础。 我们利用时间冗余，采用简单且计算成本低的模型，以适应 传感器节点有限的计算资源。这些简单模型自然只能近似有限数量的样本。因此，为了利 用数据收集中的延迟容忍特性，节点连续构建一批简单模型，以增加被近似的样本值数量。 然而，我们的方案经过优化，仅需少量节点构建这些模型批次，即可近似整个无线传感器 网络的数据。空间冗余则通过两级分层聚类加以利用。与现有文献[Jiang等2011；Pha m等2010；Gedik等 2007],不同，我们提出的聚类是基于模型而非原始样本值。基于模型 的聚类使我们能够评估节点间在较长时间内的相关性，而基于样本值的聚类仅能判断某一 时刻的相关性。因此，现有方法需要持续维护庞大的整体式簇，导致额外的能量开销。在 我们的分层聚类中，首先通过将具有高相关性的邻近节点分组形成单跳簇。这些小型单跳 簇所需维护量极小。模型批次仅在部分单跳簇上构建。这些簇构建的模型根据用户定义的 误差容限，用于近似周围簇的数据。被少数几批模型近似的单跳簇被合并，形成第二级聚 类层次。第二级聚类层次反映了单跳簇之间的动态相关性，并在每次迭代时重新构建。按 照该方案，仅需少量模型批次即可在较长时段内近似整个网络的样本值（具体时长取决于 延迟容忍限制）。模型批次被发送至汇聚节点，汇聚节点利用这些模型重建网络中每个传 感器节点的样本值。

贡献。 当前工作的贡献如下： —我们提出了一种完全去中心化的方案，除了设置时所需的少量初始参数外，无需汇聚节 点进行任何干预。—所提出的自适应建模压缩方案能够通过动态调整参数，在用户定义的 精度要求内逼近多种多样的环境属性（第4.3节）。—我们提出了一种基于自适应模型的分 层聚类新方法，用于实现空间压缩。该聚类方法能够适应环境属性在传感器网络中的分布， 以最大化空间压缩效果（第4.4节）。—我们提出了一种技术，利用各种无线传感器网络应 用中数据采集的延迟容忍特性，来增强时间和空间上的压缩性能。—我们给出了压缩的可 压缩性分析，并提供了理论上下界（第5.2节），以及详细的消息复杂度分析（第6节）。

在我们初步的延迟感知压缩ASTC方法[Alietal.2011],的基础上，我们现在提出一个 全面的框架，适用于广泛的应用，并在数据可压缩性和消息开销效率方面显著增强了界限。

本文结构如下。第2节讨论相关工作后，第3节介绍了系统模型和设计要求。第4节提出了所 提混合压缩方案。随后，第5节详细阐述了所提方案的效率与可压缩性分析，第6节评估了消息和计算成本。第7节详细说明了分析与评估结果。

2. 相关工作

本文侧重于连续数据采集，而非基于事件的无线传感器网络设计。我们的主要目标是在利用数 据采集中的延迟容忍性的同时，以传感器节点级粒度对连续数据采集进行时空压缩。尽管在无 线传感器网络的数据压缩方面已有大量研究[Nakamura等人 2007]（例如，简单聚合[ Fasolo等人 2007],、抑制[Zhou等人 2008],、滤波、TinyDB[Madden等人 2005],和 Cougar[Gehrke和Madden2004],等），但在时空压缩方面的研究工作却非常有限。我们总 结了一些关于空间和时间压缩的重要研究工作，并详细讨论了现有的时空压缩技术。

空间压缩

空间采样的目的是收集感兴趣的属性快照。空间压缩背后的核心思想是通 过限制具有相似传感器读数的相邻传感器节点传输冗余数据。Mahmudimanesh等人 [2010],、Jindal和Psounis[2006],、Solis和Obraczka[2005],以及Zhao等人[2002] 提出了一些依赖于压缩感知、空间相关模型、过滤和聚合的空间压缩技术。所有纯空间压 缩方法的主要缺点在于它们仅关注空间冗余，而忽略了时间冗余。时间分辨率取决于所实 现的快照更新机制。纯空间压缩技术通过创建新的快照或发送增量更新来简单地处理时间 冗余问题。

时间压缩

时间压缩的驱动力是利用属性值中存在的时间相关性。这些方法的核心思 想是让每个传感器节点为其传感器读数建立一个预测模型，并将该模型发送到汇聚节点。 只有当信号动态发生变化导致模型不再有效时，传感器节点才需要发送更新后的模型。 Mini等人[2005]和Zhang等人[2006]提出的方法分别基于马尔可夫链和时间序列构建模 型。这些时间压缩方案主要关注时间冗余。一些方法使用了有限形式的空间压缩（例如， 通过构建单跳簇，并仅允许簇头与汇聚节点保持模型一致性）。

时空压缩

针对无线传感器网络中时空压缩的研究非常有限。Vuran等人[2004],提 出了一种理论框架，用于建模无线传感器网络中的空间和时间相关性。该框架有助于开发 高效的介质访问和可靠事件传输协议，充分利用无线传感器网络范式中的这些内在优势特 性。然而，这项工作并未关注目标应用所需的连续数据采集。Jiang等人[2011],、Pha m等人[2010],以及Gedik等人[2007]提出了基于值的聚类机制，这些机制根据瞬时值或数 值聚合形成较大的整体式簇。因此，它们需要持续从成员节点收集数据以检查一致性，并 通过拆分和合并来维护这些簇，这在计算和能耗方面开销较大。我们提出的替代方法采用 基于模型的分层聚类，而非基于瞬时值，即：（1）单跳簇几乎不需要维护；（2）团簇无 需维护，而是在极低消息开销下进行重建。Tulone和Madden[2006]提出通过重复进行 模型构建并将其与汇聚节点同步来实现实时数据采集。但Tulone和Madden[2006]在空 间和时间可压缩性方面均存在局限性。Wang等人[2010]和Wang等人[2012]放宽了 Tulone和Madden[2006]的空间约束，从而形成大于单跳的簇。由于他们专注于实时更新， 它们仅能在有限的时间内近似一定量的数据，从而限制了时间可压缩性。另一方面，我们 所提方案的重点是针对数据收集具有延迟容忍性的应用；因此，由于时间约束较为宽松， 我们可以更高效地在空间和时间上压缩数据。Villas等人[2011] 提出了一种基于数值的方 案，以利用时间和空间相关性，并明确关注数值的实时报告。我们的方法提出一种基于模 型的方案来利用时间和空间相关性，从而扩展了时空上的可压缩性。Min和Chung [2010] 在单跳簇内使用卡尔曼滤波器进行建模，但这会在传感器节点上带来较高的计算成 本。Baek等人[2004] 提出通过分层聚合来降低能耗。Min和Chung[2010] 以及 Baek等人[2004] 都需要节点位置信息，而这可能代价过高。我们所提方案不依赖于位置 信息，并使用可在传感器节点上轻松计算的简单模型。Liu等人[2007] 和Gupta等人 [2008] 使用集中式启发式方法进行聚类和节点相关性判定。Liu等人[2007] 假设所有传 感器节点都在汇聚节点的通信范围内，或部署专用节点作为簇头，以便能够与汇聚节点直 接通信。此类假设限制了该方法[Liu等人 2007] 在通用无线传感器网络中的适用性。相 比之下，我们所提方案假设为通用的无线传感器网络部署，无需对通信范围或任何专用传 感器节点提出额外要求。此外，该方案完全是分布式的，除了最初由汇聚节点提供几个静 态参数以根据用户需求设置所提分布式方案外，不需要任何全局信息。Yoon和Shahabi [2007] 具有两种操作模式：交互模式仅限于空间压缩，而流式模式则同时执行空间和时间 压缩。Wang和Deshpande[2008] 以及Yoon和Shahabi[2007] 的流式模式均构建 概率密度函数（PDF）用于属性建模。自适应混合压缩（AHC）与概率建模在待监测属性 的统计过程假设上存在根本差异。AHC假设统计过程是动态的，且过程统计特性可能随时 发生变化。Wang和Deshpande[2008] 则假设过程统计特性保持不变，并需要手动设置 以确保正常运行。在概率建模中，一旦构建了PDF，就假设其在整个监测期间保持不变， 并可用于预测未来的样本。因此，这类方案的正确性无法得到保证。在某一时间段内构建 的PDF无法保证在属性动态变化后仍然有效，这限制了此类方案在长期连续监测中的应用。 它们还需要昂贵的长时间训练（例如，Wang和Deshpande[2008]需要15天）。我们 不预先假设系统动态已知，而是根据无线传感器网络属性的变化动态构建模型。因此，我 们的技术不仅能跟踪任何变化的属性动态，还能在动态发生意外变化时进行调整。在我们 先前的工作[Ali等人 2011], 中，我们提出了利用模型和聚类的时空压缩方法。本文在 Ali等人[2011] 的基础上进行了改进，提供了灵活选择多种模型而非单一固定模型的能力、 动态时间压缩范围，以及相比严格时间同步更为宽松的时间同步要求。

另一种重要的无线传感器网络压缩方法基于变换压缩。在变换压缩中，对感知信号应 用线性变换，生成更易于压缩的数据版本，从而减少需要传输到汇聚节点的数据量[ Duarte等 2012]。无线传感器网络中的变换压缩和模型驱动类数据压缩方法均利用感知信 号的可压缩性来减少 尽管采用的方法不同，但都会减少网络内传输量。在本文中，我们将变换压缩作为一种重 要的无线传感器网络数据压缩相关方法进行研究，并将我们的工作与一种典型的变换压缩 实现方式进行比较。分布式变换压缩（DTC）方法（也称为分布式变换编码技术）基于以 下事实：从自然现象中记录的原始数据（例如无线传感器网络所感知的数据）在某些线性 变换下是可压缩的[Duarte等人 2012]。对原始数据进行变换和压缩后，将压缩后的数据 发送到汇聚节点。汇聚节点随后应用逆变换以恢复原始数据。

总之，现有的混合方法需要预先知道信号及其统计特性（动态特性），需要位置信息， 是部分/完全集中的，或在聚类中使用瞬时值而非可计算模型。所有现有方案的共同点是它 们都针对实时/即时数据采集。除了[Alietal. 2011],之外，没有其他现有工作利用许多应 用固有的延迟容忍性，因而失去了效率提升潜力。相比之下，我们的方法是自适应的，不 需要位置信息，是完全去中心化的，使用简单且易于计算的模型，并利用延迟容忍性以最 大化数据收集。

3. 预备知识

3.1. 系统模型

我们考虑一个由N个静态传感器节点{S1, S2,…, SN}和一个静态汇聚节点组成的传统无线传 感器网络系统模型。我们假设节点的时钟是同步的，例如使用Faizulkhakov[2007]方法 实现。传感器节点每隔 τ个时间单位同时且周期性地采样环境属性。这种同步采样使得节 点可以运行占空比循环以实现最大化的能量效率，但这不在本文讨论范围内。汇聚节点具 有足够的能力来存储大量数据。传感器节点为电池供电，且具有有限的存储和处理能力。 无线传感器网络部署遵循任意节点分布，其空间节点密度根据连通性、覆盖范围、容错性 和感知需求而变化。我们假设存在可靠的端到端数据传输服务（如Shaikh等人的[2010],） 用于将消息从传感器节点传输到汇聚节点，并采用确认机制来确保邻近节点之间的消息传 递。

3.2. 设计要求

我们的目标是为连续延迟容忍数据采集（即现象监测或环境属性监测）在保证精度的前提 下最大化时空数据压缩比。为了实现这些目标，所提方案必须能够在汇聚节点上根据采集 到的压缩数据，在应用驱动的误差范围内重构每个传感器节点的信号（样本值），同时带 来最小的带宽和能量开销。所提方案应能适应变化的属性动态，并且独立于网络特性，如 节点分布、拓扑结构和路由协议。数据压缩模型应在资源受限的传感器节点上高效可计算。

4. 所提出的自适应时空压缩

我们提出了一种利用应用延迟容忍特性的去中心化自适应混合压缩技术。如图1所示，处于 单跳距离内的邻近节点在样本值上通常表现出持续的高相关性。然而，在较长时间窗口下 观察时，距离较远的节点之间（即单跳簇之间）的相关性通常是非持续且动态变化的。这 种邻近节点间与远距离节点间相关性的不对称性

距离较远的节点使得时空压缩成为一个具有挑战性的问题。现有文献通过以下方式应对这 种不对称性：将建模限制在单跳簇内[Tulone和Madden 2006],，假设属性动态保持不变 [Chu等 2006],，需要汇聚节点的协助[Liu等2007；Gupta等 2008]，或基于瞬时值而 非模型进行聚类[Jiang等2011；Pham等2010；Gedik等 2007]。

我们提出在两个阶段利用空间冗余，即：（1）主动形成通常具有高度相关性的单跳簇， 以及（2）将单跳簇合并为更大的区域/簇。我们的空间压缩方法不同于当前的方法，例如 Gedik等人[2007]和Yoon与Shahabi[2007]的方法。这些方法形成大型整体式簇，容易 频繁重新配置，从而导致较高的维护开销。我们通过在一跳簇上构建简单模型来利用时间 冗余。

4.1. AHC方案指南

鉴于无线传感器网络部署的冗余性以及感知属性的相关性，所提方案在三个阶段执行时空压缩： —阶段1：单跳簇形成。—阶段2：簇上的时 间建模。—阶段3：合并单跳簇。

在阶段1中，具有相关传感器读数的传感器节点的邻域根据属性值的短期历史形成小型 单跳簇，以利用强烈的局部相关性。根据部署的传感器密度，单跳簇可能包含多达十几个 节点。

在阶段2中，我们通过在少量簇上构建模型来利用时间相关性，这些簇被称为主簇（如 图2中带皇冠的所示）。每个构建的模型最初仅限于相应的主簇，并近似该主簇所有成员传 感器节点的采样值。

在阶段3中，我们提出机制，利用在主簇上构建的模型来近似周围单跳簇中节点的采样 值。主簇将模型发送到其邻近簇。簇成员将其采样值拟合到接收到的模型，并相应地选择 接受或拒绝该模型。接受该模型的簇合并形成一个相关区域（更大的簇），并进一步将模 型传播到该区域边界上的单跳簇。

按照该方案，仅需在主簇上构建少量模型即可在空间和时间上近似整个网络。由此产 生的空间压缩是一种两级分层聚类。第一级和第二级层次结构分别在阶段1和阶段3中形成。 阶段1仅执行一次，而阶段2和阶段3则重复执行，以持续建模采样值并适应变化的动态特性。 下文将详细说明这三个阶段。

4.2. 阶段1：单跳簇形成

与现有方法不同，我们首先构建小型单跳簇而非大型整体式簇，以利用强烈的局部空间相 关性。随后（阶段3），将这些单跳簇合并形成更大的簇，以建模单跳簇之间的动态相关性。 相比构建和维护较小的单跳簇，构建和维护大型整体式簇会带来较高的开销，这一点我们 将在第4.4节进一步说明。由于簇的形成在无线传感器网络中已得到广泛研究[Abbasi和 Younis 2007],，因此我们仅简要描述单跳簇的形成过程。

单跳簇的形成基于候选簇头节点所传输的属性值短期历史的相似性。网络中的所有节 点最初都是簇头的候选者。汇聚节点下发任务，要求对环境进行采样，并将压缩后的采样 值发送回汇聚节点。各节点等待一段随机时间t1h，当t1h到期后，某节点即成为簇头，并向 其单跳邻居发送“加入请求”以及一组其采样值。在此期间，接收到加入请求的节点不再 发送加入请求。如果多个节点在其彼此的单跳邻域内同时发送加入请求，则具有较低ID的 节点撤销其请求。此外，由于某个节点可能同时是多个非相互单跳邻居节点的单跳成员， 因此仍可能收到来自其他节点的加入请求。

接收到加入请求的节点将其接收的值与自身的采样值进行比较。若其采样值与接收值 之间的差异在应用/用户设定的精度要求范围内，则该节点加入相应的簇。由于碰撞或隐藏 终端问题，候选簇发送的请求偶尔可能未被其单跳簇成员接收到{Tobagiand Kleinrock}。无法加入任何簇的节点（无论是因为未接收到请求，还是因为误差过大）将 自行发起簇形成请求。

后续的请求节点可以被已存在的簇头认领，如果该簇头发现请求节点的值在给定阈值 范围内，以补偿丢失的请求消息。表I总结了我们的簇符号表示。相应地，我们定义一个单 跳簇（Ci）由一个簇头节点（SCH）和“r”个成员节点（Si）组成，这些成员节点距离簇 头一跳，即，Ci={SCH, S1, S2,…, Sr}, ∧∀Si ∈Cihopdist(SCH, Si)= 1（其中 hopdist()返回两个节点之间的跳数距离）。一个簇的成员可能能够监听多个簇头，但仅属 于一个簇，即Ci ∩ Cj= ∅，i =j。

每个单跳簇头发现其周围的直接一跳邻近簇（CN）。在发现过程中，簇头之间交换簇 ID（与簇头ID相同）以及簇头到汇聚节点的跳数距离。它们还识别出用于两个邻近簇头之 间通信的节点，这些节点被称为网关节点，如图3所示。单跳簇形成过程仅执行一次。为了 保持这些簇内节点之间的相关性，我们不会显式地刷新单跳簇。相反，我们以自适应的方 式设计阶段2和阶段3，使得单跳簇的重组能够进行

符号	描述
Si	ith传感器节点
SCH	簇头
Ci	ith簇
r	簇成员数量
CN	邻近簇列表

4.3. 阶段2：单跳簇中的时间建模

我们现在详细阐述一种时间压缩方案，用于对传感器节点的采样值进行建模。我们将在第 4.3.8节中使用所开发的时间压缩方法，首先对单跳簇中节点的采样值进行建模，并在第 4.4节中将该建模扩展到单跳簇之外。该方案的设计使得模型构建仅由主簇执行（主簇的选 择在第4.4.1节中说明），而其余簇则使用主簇构建的模型来近似其采样值。

根据第3.2节的需求，我们要求模型具备以下特性：(a)计算开销小，便于估计；(b)低 内存需求；(c)必须具有自适应性，以适应多变的属性动态。基于这些需求，我们提出了时 间压缩方案。表II总结了建模所需的符号。

符号	描述
v(t)	在时间t的采样值
vˆ(t)	时间t的近似值
V(t)或V	用于训练模型的采样值队列（训练队列）
Vˆ(t)或 Vˆ	估计值
T	训练队列长度
p	AR模型的模型阶数
φ	模型参数
i	ith模型
W	模型的近似窗口
W	模型缓存（模型集合）
Vˆ	模型缓存估计样本集
m#	模型数量在中
ε	误差阈值
O#max	每个节点每个模型允许的最大异常值数量

4.3.1. 分段建模

由于（a）节点资源有限和（b）未知的属性动态，使用计算成本较高的模型来逼近通常在采样属性中观察到的通用模式，在传感器节点上通常是不可行的。我们通过表示采样数据来形式化时间压缩 将传感器节点的采样值建模为一个无限的一元时间序列。为了对传感器节点上的采样值进 行建模，我们可以将采样值（时间序列）分解为有限持续时间的段，我们将其称为训练队 列，并表示为V(t)，用于估计模型参数

$$
V(t)=(v(t), v(t −1), v(t −2),…, v(t − T+ 1)), (1)
$$

其中， v(t)表示传感器节点在时间t 采集的数据，T 表示训练队列的长度（第4.3.3节）。 每个段可以建模为一个线性分量和一个随机分量。

4.3.2. 随机分量估计

一个突出的设计目标是支持广泛的应用。因此，它需要在不依赖于采样属性值的统计过程的前提下进行设计。为此，除了要求该过程为弱平稳外，我们不对底层过程做任何假设，这对于物理过程通常是成立的[Ljung 1998]。这使得人们可以将 随机分量建模为自回归移动平均（ARMA）模型的线性差分方程。由于ARMA模型中的移 动平均（MA）分量计算相对复杂，为了降低计算复杂度，我们将估计限制在自回归（ AR）模型上，表示如下：

$$
x(t)= φ1x(t −1)+ ···+ φpx(t −p)+ w(t)=
p
∑
i=1
φix(t −i)+ w(t), (2)
$$

其中，x(t)是信号的随机分量， w(t)是均值为零、方差为σ 2(WN(0, σ 2))的白噪声序列， φ为 模型系数，p 为模型阶数且p ∈ N。我们将使用公式(2)构建的模型表示为(x)（或简写为）。

4.3.3. 模型构建

为了构建模型，一个节点维护一个包含V={v1, v2,…, vT}个T采样值的训练队列。通过以下方式调整自回归模型参数：(a)估计拟合误差（e()），以及(b)最小化估计误差。自回归模型拟合误差e()按均方误差意义最小化，如以下所示

$$
∂
∂φk
e()2= ∂ ∂
⎛⎜⎝ T ∑
i=p+1
⎛⎝x(i)− p
∑
j=1
φj x(i −j) ⎞⎠2⎞⎟⎠= 0. (3)
$$

由模型近似得到的样本值为

$$
vˆ(t)= μ+
p
∑
i=1
φi(v(t −i)−μ), (4)
$$

其中，vˆ(t)是估计的样本值， μ是序列均值。我们将ˆV表示为近似值集合，其中ˆV={ˆ v1, vˆ2… vˆW }；W是估计值的数量，称为近似窗口（详见第4.3.6节）。

4.3.4. 基于异常检测的分段自适应建模（AM）

由于我们假设采样值的统计过程是未知的， 因此模型必须具备根据变化的统计动态特性进行自适应的自然前提。这种适应性可以通过 向模型提供反馈以适应新的动态特性来实现。然而，由于需要持续将包含新模型参数的更 新传输到汇聚节点，导致消息开销增加，因此该方法开销较大。为此，我们采用一种基于 异常值而非模型参数的自适应更新算法。

异常检测。 无法通过模型近似表示的样本值可以被容忍并归类为异常值。如果 α是最 大容许的估计误差，则估计值必须位于[v−α, v+ α]之间。如果某个估计值不在该界限范围 内，节点将用原始采样值替换该值，并将其分类为异常值。异常值应单独上报至汇聚节点， 以实现准确的信号重构。节点可通过以下方式判断一个估计值是否为异常值

$$
vˆ(t)={ v(t),if ∣ ∣vˆ(t)− v(t)∣∣> α;
vˆ(t), otherwise.
(5)
$$

一跳簇头收集并将其簇成员的异常值报告给汇聚节点，以在 α范围内保持精度。图4展示了 基于公式(5)的自适应建模的框图（z−1表示时间延迟）。

估计值相关的误差上界和误差概率可由引理4.1给出（详细证明见Tulone和 Madden[2006]）。

LEMMA 4.1. 令 α= νσ，其中 ν是大于1的应用指定实常数；实际采样值vi(t)包含在[vˆ (t) −α，vˆ(t)+ α]中的误差概率至多为1/ν2。

模型失效与异常值上限。 如果一个模型无法在定义的精度界限内近似采样值，则该模 型失效。当精度界限不满足时，会产生异常值，从而增加消息开销。我们认为一个模型在 产生的异常值不超过最大数量（O#max）时是有效的。节点基于构建的模型使用公式(4)来近 似采样值，并使用公式(5)统计异常值。如果某个模型产生的异常值超过O#max，则该模型失 效，必须重建新模型。通过采用此方案，我们能够控制生成的异常值的最大数量，满足精 度要求，并避免模型不必要的重构。

我们已经讨论了标准建模技术、如何使其具有自适应性，并提议使用简单的AR模型以 满足最低的计算和内存需求。然而，我们尚不清楚何种阶数的AR模型能够最佳地逼近样本 值。因此，在下一节中，我们将讨论如何选择能够在满足资源约束的同时，以最小误差逼 近采样值并产生最少异常值的模型。

4.3.5. 通过动态模型阶数选择实现动态自适应建模（DAM）

我们开发了一种自适应建模 方案，传感器节点使用该方案动态选择最能逼近采样值并减少消息开销的合适模型阶数。 该方案还避免了不必要的高阶计算。

传感器

定义1. 模型的近似窗口（W ）是指该模型（）在允许O#max个异常值的情况下，能 够在所需精度界限内近似的样本数量。

近似窗口取决于精度界限、允许的异常值、模型阶数以及属性动态特性。提高容许的 精度界限、最大允许异常值和模型阶数通常会增加近似窗口。

然而，由于使用线性模型，信号中不断增加的非线性通常会减小近似窗口，而精度界 限则根据用户需求固定。为限制消息开销，最大允许异常值数量在设计时即被固定。模型 阶数动态选择以实现最佳压缩（第4.3.5节）。因此，在给定精度要求和异常值边界的情况 下，属性动态决定了特定模型的近似窗口。

构建的模型用于近似其训练所用的值，即训练队列（V）。近似值集合表示为ˆV(ˆV ={vˆ(t),vˆ(t −1)…vˆ(t −W+1)})。由于动态特性，一个近似窗口的样本数量可能会变化。 在图5中，我们说明了动态近似窗口的概念。尾部样本值使用基于训练采样值得到的模型 （）进行估计。估计值的数量（模型近似窗口）记为W。W的估计值数量可以根据底 层过程的动态特性、误差阈值以及最大允许异常值，从少于训练长度的近似样本到超出训 练长度的样本而变化。

图5描述了各种情况；例如，ˆV1将样本估计到训练向量长度ˆV1,，而ˆV2短于V2,，并 且ˆV4超出了训练长度V4。在ˆV V的情况下，当ˆV中的估计值少于训练样本长度时，训 练集中未被估计的值将传递给下一个训练集。例如，在图5中，V2中未被ˆV2估计的样本被 传递给V3以训练下一个模型。有时，一个模型可能已经估计了训练集中的所有样本值（例 如，ˆV4），但异常值的数量仍少于O#max。在这种情况下，该模型将继续逼近后续的值（即 预测），直到异常值的数量少于O#max为止。

我们现在开发一种机制来构建一批模型，从而无需发送 indi单个模型，一批模型可以通过一条消息发送到汇聚节点。

4.3.7. 最大时间压缩与模型缓存

我们假设数据传输可以根据应用程序指定的延迟容忍度进行延迟。 我们用

以可收集并用于构建模型缓存进而上报至汇聚节点的样本数来表示应用延迟容忍性。该延 迟由模型缓存所近似的总样本数表示，记为W。容忍延迟，即ˆV的长度，通常比简单自 回归模型的近似窗口长几个数量级。一般情况下，节点需要使用多个模型才能近似整个采 样数据的长度。

主簇头构建了一个连续的模型批次，称为模型缓存。一个传感器节点收集包含T个样 本的训练数据（V），用于如第4.3.3节所述训练模型。所构建的模型用于近似这些样本 （ˆV）。随后的样本则用于构建一个新的训练队列。该新的训练队列再次以相同方式用于 构建下一个模型。此过程持续重复，直到近似了W个样本为止。我们将用于近似W个样 本的m#个模型的集合定义为模型缓存，记作 ，并定义为={1,2,…m#}。图6中也 展示了模型缓存的构建过程。由于存在延迟容忍以及模型缓存机制，我们无需反复构建模 型、将其发送至汇聚节点，并在前一个模型失效后发送新模型。这种方案将需要反复向汇 聚节点传输模型参数。通过构建模型缓存，主簇避免了报告每一个模型，从而避免了此类 重复重传，显著降低了消息开销。因此，我们能够增大时间压缩窗口，处理非线性，降低 消息开销，节省能量，同时仍使用简单且计算成本低的模型。接下来，在第4.2节中，我们 将证明由模型缓存估计的样本误差保持在用户定义的误差阈值之内。

LEMMA 4.2. 对于一个模型缓存 ，属于近似模型缓存值vˆ(t)(∧vˆ(t) ∈ˆV(t))的实际采样值 v (t)包含在[vˆ(t)−α，vˆ(t)+α]中。

PROOF。 模型缓存是一组m#AR模型，即 ={1,2,…m#}。根据引理4.1，每个 模型i ∈ 的采样值包含在[vˆi( t) − α，vˆi( t)+ α]中（其中ˆvi 是使用模型i得到的近似 采样值）。因此，由模型缓存i近似得到的采样值包含在[vˆ(t)−α，vˆ(t)+α]中。

迄今为止开发的时间压缩方案可被任何传感器节点用来动态确定最能近似其采样值的 模型缓存。然而，我们所设计的所提方案仅使网络中的少数节点执行此操作。

属于主簇的网络实际执行所提方案来构建模型。接下来，我们描述主簇的簇头如何利用所 开发的技术来构建模型。主簇的选择以及其他簇如何利用在主簇上构建的模型缓存进行近 似的方法将在阶段3中进一步讨论。

4.3.8 主簇模型构建

我们压缩方案的基本原理是，仅有一个节点（或少数几个节点）应 构建一个模型，以在精度界限内精确逼近其周围簇中尽可能多的节点。因此，我们在主簇 上构建模型，这些模型不仅用于逼近主簇内节点的采样值，还用于逼近主簇周围簇中节点 的采样值。主簇的选择将在第4.4.1节中讨论。一旦选定主簇，将按前述方式构建模型缓存。 为了使在簇头构建的模型缓存能够逼近其他传感器节点的采样值，我们需要定义一种 用于衡量两个传感器节点之间采样值相似性的度量方法。

定义2. 如果来自传感器si和sj的近似采样值分别由ˆvi(t)和vˆj(t)给出，则使用传感器节 点s的模型缓存(i)来逼近第i个传感器节点采样值的逼近损失可表示为L(t)ˆ(t)ˆ(t)。

为了满足用户的精度要求，我们仅在两个属性值的逼近损失被 β限定时，才将其定义 为相似。因此，如果传感器节点si和sj满足逼近损失界限，即Lij(t) ≤ β，则这两个节点 之间的逼近误差可由引理4.3给出。

LEMMA 4.3. 在满足逼近损失界限的情况下，第i个传感器节点Si使用来自第j个传感器 节点Sj的模型缓存时的最大逼近误差最多为 α+ Lij=α+ β，且误差概率小于 1/ν2。

PROOF。 假设传感器节点si构建一个模型缓存 i，并且传感器节点sj使用i来估计其采样值，使得 在任意给定时间t，对于模型缓存的长度，sj和