广义状态平均无线电能传输系统建模

关于WPT系统建模的一些笔记，在 CSDN 学到很多，现分享给大家，之前有看到过一篇博文， 内容语焉不详，对读者也很不客气，希望这篇博文对大家有用！

Hierarchical multiobjective H-infinity robust control design for wireless power transfer system using genetic algorithm

[!info] Bibliography
[1] M. Yang, Y. Li, H. Du, C. Li, and Z. He, “Hierarchical multiobjective H-infinity robust control design for wireless power transfer system using genetic algorithm,” IEEE Transactions on Control Systems Technology, vol. 27, no. 4, pp. 1753–1761, 2018, doi: 10.1109/TCST.2018.2814589 .

Information

Key	Value
Date	2018-01
Author	Mingkai Yang, Yanling Li, Hao Du, Chen Li, Zhengyou He
Journal	#IEEE-Transactions-on-Control-Systems-Technology
DOI	10.1109/TCST.2018.2814589
Publisher	IEEE Transactions on Control Systems Technology

System modeling

The states of dynamic components can be approximated by their first-order or zero-order:
$$\begin{array}{c}\begin{array}{rl}{i}_{L_p}& ={⟨i_{L_p}⟩}_1{e}^{j\omega t}+{⟨i_{L_p}⟩}_{-1}{e}^{-j\omega t}\\ u_{C_p}& ={⟨u_{C_p}⟩}_1{e}^{j\omega t}+{⟨u_{C_p}⟩}_{-1}{e}^{-j\omega t}\\ i_{L_s}& ={⟨i_{L_s}⟩}_1{e}^{j\omega t}+{⟨i_{L_s}⟩}_{-1}{e}^{-j\omega t}\\ u_{C_s}& ={⟨u_{C_s}⟩}_1{e}^{j\omega t}+{⟨u_{C_s}⟩}_{-1}{e}^{-j\omega t}\\ u_{C_f}& ={⟨u_{C_f}⟩}_0\end{array}\end{array}$$

• $\omega =2\pi f$
• $⟨x{⟩}_n=\frac{1}{T}{\int }_0^{T}x{e}^{-jn\omega t}dt$ is the $n$th-order complex Fourier series coefficient.

[!note]

Another form:
$$\begin{array}{c}\begin{array}{rl}{i}_{L_p}& =a_{1i_{L_p}}\cos (\omega t)+b_{1i_{L_p}}\sin (\omega t)\\ u_{C_p}& =a_{1u_{C_p}}\cos (\omega t)+b_{1u_{C_p}}\sin (\omega t)\\ i_{L_s}& =a_{1i_{L_s}}\cos (\omega t)+b_{1i_{L_s}}\sin (\omega t)\\ u_{C_s}& =a_{1u_{C_s}}\cos (\omega t)+b_{1u_{C_s}}\sin (\omega t)\\ u_{C_f}& =a_{1u_{C_f}}\cos (\omega t)+b_{1u_{C_f}}\sin (\omega t)+a_{0u_{C_f}}\end{array}\end{array}$$
where $⟨x{⟩}_1=\frac{1}{2}(a_{1x}-i{b}_{1x})$
$$\begin{array}{rl}{a}_n& =\frac{2}{T}{\int }_0^{T}x(t)\cos (t)\mathrm{d}t\\ b_n& =\frac{2}{T}{\int }_0^{T}x(t)\sin (t)\mathrm{d}t\\ a_0& =\frac{2}{T}{\int }_{t-T}^{t}x(t)\mathrm{d}t\end{array}$$

[!note]
$$\{\begin{array}{rl}{L}_p\frac{d{i}_{L_p}}{dt}-M\frac{d{i}_{L_s}}{dt}+R_p{i}_{L_p}-S_i{U}_{\text{in}}+u_{C_p}& =0\\ L_s\frac{d{i}_{L_s}}{dt}+R_s{i}_{L_s}+u_{C_s}+S_r{u}_{C_f}-M\frac{d{i}_{L_p}}{dt}& =0\end{array}$$
Using the second equation:
$$\frac{d{i}_{L_s}}{dt}=\frac{1}{L_s}\left(-R_s{i}_{L_s}-u_{C_s}-S_r{u}_{C_f}+M\frac{d{i}_{L_p}}{dt}\right)$$
Substituting it to the first equation:
$$\begin{array}{rl}{L}_p\frac{d{i}_{L_p}}{dt}-M\frac{1}{L_s}\left(-R_s{i}_{L_s}-u_{C_s}-S_r{u}_{C_f}+M\frac{d{i}_{L_p}}{dt}\right)+R_p{i}_{L_p}-S_i{U}_{\text{in}}+u_{C_p}& =0\\ L_p\frac{d{i}_{L_p}}{dt}+\frac{M}{L_s}{R}_s{i}_{L_s}+\frac{M}{L_s}{u}_{C_s}+\frac{M}{L_s}{S}_r{u}_{C_f}-\frac{M^2}{L_s}\frac{d{i}_{L_p}}{dt}+R_p{i}_{L_p}-S_i{U}_{\text{in}}+u_{C_p}& =0\\ \frac{d{i}_{L_p}}{dt}\left(L_p-\frac{M^2}{L_s}\right)+i_{L_s}\frac{M}{L_s}{R}_s+R_p{i}_{L_p}+\frac{M}{L_s}{u}_{C_s}+\frac{M}{L_s}{S}_r{u}_{C_f}-S_i{U}_{\text{in}}+u_{C_p}& =0\\ \frac{d{i}_{L_p}}{dt}\left(\frac{L_p{L}_s-M^2}{L_s}\right)+i_{L_s}\frac{M}{L_s}{R}_s+R_p{i}_{L_p}+\frac{M}{L_s}{u}_{C_s}+\frac{M}{L_s}{S}_r{u}_{C_f}-S_i{U}_{\text{in}}+u_{C_p}& =0\\ i_{L_s}\frac{M}{L_s}{R}_s+R_p{i}_{L_p}+\frac{M}{L_s}{u}_{C_s}+\frac{M}{L_s}{S}_r{u}_{C_f}-S_i{U}_{\text{in}}+u_{C_p}& =\frac{d{i}_{L_p}}{dt}\left(\frac{M^2-L_p{L}_s}{L_s}\right)\\ \left(\frac{L_s}{M^2-L_p{L}_s}\right)\left[i_{L_s}\frac{M}{L_s}{R}_s+R_p{i}_{L_p}+\frac{M}{L_s}{u}_{C_s}+\frac{M}{L_s}{S}_r{u}_{C_f}-S_i{U}_{\text{in}}+u_{C_p}\right]& =\frac{d{i}_{L_p}}{dt}\\ \left(\frac{1}{M^2-L_p{L}_s}\right)[i_{L_s}M{R}_s+R_p{L}_s{i}_{L_p}+M{u}_{C_s}+M{S}_r{u}_{C_f}-L_s{S}_i{U}_{\text{in}}+L_s{u}_{C_p}]& =\frac{d{i}_{L_p}}{dt}\\ \frac{1}{\lambda }[M{R}_s{i}_{L_s}+R_p{L}_s{i}_{L_p}+M{u}_{C_s}+M{S}_r{u}_{C_f}-L_s{S}_i{U}_{\text{in}}+L_s{u}_{C_p}]& =\frac{d{i}_{L_p}}{dt}\\ \frac{1}{\lambda }[R_p{L}_s{i}_{L_p}+L_s{u}_{C_p}+M{R}_s{i}_{L_s}+M{u}_{C_s}+M{S}_r{u}_{C_f}-L_s{U}_{\text{in}}{S}_i]& =\frac{d{i}_{L_p}}{dt}\end{array}$$

$$\begin{array}{c}\begin{array}{rl}\frac{d{⟨i_{L_p}⟩}_1}{dt}=& {\lambda }^{-1}(R_p{L}_s{⟨i_{L_p}⟩}_1+L_s{⟨u_{C_p}⟩}_1+M{R}_s{⟨i_{L_s}⟩}_1\\ & +M{⟨u_{C_s}⟩}_1+M{⟨S_r{u}_{C_f}⟩}_1-L_s{U}_{\mathrm{in}}{⟨S_i⟩}_1)-j\omega {⟨i_{L_p}⟩}_1\\ \frac{d{⟨u_{C_p}⟩}_1}{dt}=& C_p^{-1}{⟨i_{L_p}⟩}_1-j\omega {⟨u_{C_p}⟩}_1\\ \frac{d{⟨i_{L_s}⟩}_1}{dt}=& {\lambda }^{-1}(M{R}_p{⟨i_{L_p}⟩}_1+M{⟨u_{C_p}⟩}_1+R_s{L}_p{⟨i_{L_s}⟩}_1\\ & +L_p{⟨u_{C_s}⟩}_1+L_p{⟨S_r{u}_{C_f}⟩}_1-M{U}_{\mathrm{in}}{⟨S_i⟩}_1)-j\omega {⟨i_{L_s}⟩}_1\\ \frac{d{⟨u_{C_s}⟩}_1}{dt}=& C_s^{-1}{⟨i_{L_s}⟩}_1-j\omega {⟨u_{C_s}⟩}_1\\ \frac{d{⟨u_{C_f}⟩}_0}{dt}=& C_f^{-1}{⟨S_r{i}_{L_s}⟩}_0-C_f^{-1}{R}_{\mathrm{dc}}^{-1}{⟨u_{C_f}⟩}_0\end{array}\end{array}$$

• $\lambda =M^2-L_p{L}_s$
• $\frac{d⟨x{⟩}_n(t)}{dt}={⟨\frac{dx}{dt}⟩}_n(t)-jn\omega ⟨x{⟩}_n(t)$
• $S_i(t)=\mathrm{sign}(\sin (\omega t))$ , $⟨S_i{⟩}_1=-i\frac{2}{\pi },⟨S_i{⟩}_1^R=0,⟨S_i{⟩}_1^I=\frac{2}{\pi }$， $S_i(t)\approx \frac{4}{\pi }\sin (\omega t)$
• $S_r(t)=\mathrm{sign}(\sin (\omega t+\pi /2))$, $⟨S_r{⟩}_1=\frac{2}{\pi },⟨S_r{⟩}_1^R=\frac{2}{\pi },⟨S_r{⟩}_1^I=0$, $S_r(t)\approx \frac{4}{\pi }\cos (\omega t)$

[!note]
$$\begin{array}{rl}{S}_i(t)& =\sum _{n=0}^{\infty }⟨S_i{⟩}_n{e}^{-jn\omega t}\\ ⟨S_i(t){⟩}_1& =\frac{1}{T}{\int }_{-T/2}^{T/2}{S}_i(t)e^{-j\omega t}dt\\ & =\frac{1}{T}{\int }_{-T/2}^{T/2}\text{sign}(\sin (\omega t))e^{-j\omega t}dt\\ & =\frac{1}{T}\left({\int }_{-T/2}^0-e^{-j\omega t}dt+{\int }_0^{T/2}{e}^{-j\omega t}dt\right)\\ & =\frac{1}{T}\left({\int }_{-T/2}^0-e^{-j\omega t}dt+{\int }_0^{T/2}{e}^{-j\omega t}dt\right)\\ & =\frac{\omega }{2\pi }\left({\frac{1}{j\omega }{e}^{-j\omega t}|}_{-\frac{\pi }{\omega }}^0-{\frac{1}{j\omega }{e}^{-j\omega t}|}_0^{\frac{\pi }{\omega }}\right)\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }[(1-e^{j\pi })-(e^{-j\pi }-1)]\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }[2-(e^{j\pi }+e^{-j\pi })]\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }[2-2\cos (\pi )]\\ & =\frac{1}{j2\pi }4\\ & =-j\frac{2}{\pi }\end{array}$$
since $c_1=\frac{1}{2}(a_1-i{b}_1)$, we have $b_1=\frac{4}{\pi }$, $S_i\approx b_1\sin (\omega t)=\frac{4}{\pi }\sin (\omega t)$

Calculate using the below code (in Mathematica):

f = Sign[Sin[w t]];
T = 2 Pi / w;
c1 = 1/T Integrate[f Exp[-I w t], {t, 0, T}]
a1 = 2 Re[c1]
b1 = -2 Im[c1]

$$\begin{array}{rl}⟨S_r(t){⟩}_1& =\frac{1}{T}{\int }_{-T/2}^{T/2}{S}_r(t)e^{-j\omega t}dt\\ & =\frac{1}{T}{\int }_{-T/2}^{T/2}\text{sign}\left(\sin \left(\omega t+\frac{\pi }{2}\right)\right)e^{-j\omega t}dt\\ & =\frac{1}{T}{\int }_{-T/2}^{T/2}\text{sign}(\cos (\omega t))e^{-j\omega t}dt\\ & =\frac{1}{T}\left({\int }_{-T/2}^{-T/4}-e^{-j\omega t}dt+{\int }_{-T/4}^{T/4}{e}^{-j\omega t}dt+{\int }_{T/4}^{T/2}-e^{-j\omega t}dt\right)\\ & =\frac{\omega }{2\pi }\left({\frac{1}{j\omega }{e}^{-j\omega t}|}_{-\frac{\pi }{\omega }}^{-\frac{\pi }{2\omega }}-{\frac{1}{j\omega }{e}^{-j\omega t}|}_{-\frac{\pi }{2\omega }}^{\frac{\pi }{2\omega }}+{\frac{1}{j\omega }{e}^{-j\omega t}|}_{\frac{\pi }{2\omega }}^{\frac{\pi }{\omega }}\right)\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }\left[\left(e^{j\frac{\pi }{2}}-e^{j\pi }\right)-\left(e^{-j\frac{\pi }{2}}-e^{j\frac{\pi }{2}}\right)+\left(e^{-j\pi }-e^{-j\frac{\pi }{2}}\right)\right]\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }\left[(e^{-j\pi }-e^{j\pi })+2\left(e^{j\frac{\pi }{2}}-e^{-j\frac{\pi }{2}}\right)\right]\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }\left[-2j\sin (\pi )+4j\sin \left(\frac{\pi }{2}\right)\right]\\ & =\frac{\omega }{2\pi }\frac{1}{j\omega }4j\\ & =\frac{2}{\pi }\end{array}$$

$a_1=2⟨S_r(t){⟩}_1^R$, $S_r\approx a_1\cos (\omega t)=\frac{4}{\pi }\cos (\omega t)$

Calculate using the below code:

f  = Sign[Sin[w t + Pi / 2]];
T  = 2 Pi / w;
c1 = 1/T Integrate[f Exp[-I w t], {t, 0, T}]
a1 = 2 Re[c1]
b1 = -2 Im[c1]

[!warning]

Here using the triangular form of transformation will be more convenient !!!
$$\begin{array}{rl}⟨S_r(t){⟩}_1^R& =\frac{1}{T}{\int }_{-T/2}^{T/2}{S}_r(t)\cos (\omega t)dt\\ & =\frac{2}{\pi }\\ ⟨S_r(t){⟩}_1^I& =\frac{1}{T}{\int }_{-T/2}^{T/2}{S}_r(t)\sin (\omega t)dt\\ & =0\end{array}$$
Code:

f = Sign[Sin[w t + Pi / 2]]
T = 2 Pi / w
a1half = 1/T Integrate[f Cos[w t], {t, 0, T}]
b1half = 1/T Integrate[f Sin[w t], {t, 0, T}]

[!note]

Taking the first equation as an example:
$$\begin{array}{rl}\frac{d⟨i_{L_p}{⟩}_1}{dt}& ={\lambda }^{-1}(R_p{L}_s⟨i_{L_p}{⟩}_1+L_s⟨u_{C_p}{⟩}_1+M{R}_s⟨i_{L_s}{⟩}_1+M⟨u_{C_s}{⟩}_1+M⟨S_r{u}_{C_f}{⟩}_1-L_s{U}_{\mathrm{in}}⟨S_i{⟩}_1)-j\omega ⟨i_{L_p}{⟩}_1\\ \frac{d⟨i_{L_p}{⟩}_1^R}{dt}& ={\lambda }^{-1}\left(R_p{L}_s⟨i_{L_p}{⟩}_1^R+L_s⟨u_{C_p}{⟩}_1^R+M{R}_s⟨i_{L_s}{⟩}_1^R+M⟨u_{C_s}{⟩}_1^R+M⟨S_r{u}_{C_f}{⟩}_1^R-L_s{U}_{\mathrm{in}}⟨S_i{⟩}_1^R\right)+\omega ⟨i_{L_p}{⟩}_1^I\\ & ={\lambda }^{-1}\left[R_p{L}_s⟨i_{L_p}{⟩}_1^R+L_s⟨u_{C_p}{⟩}_1^R+M{R}_s⟨i_{L_s}{⟩}_1^R+M⟨u_{C_s}{⟩}_1^R+M(⟨S_r{⟩}_0⟨u_{C_f}{⟩}_1^R+⟨S_r{⟩}_1^R⟨u_{C_f}{⟩}_0)-L_s{U}_{\mathrm{in}}⟨S_i{⟩}_1^R\right]+\omega ⟨i_{L_p}{⟩}_1^I\\ & =⟨i_{L_p}{⟩}_1^R{\lambda }^{-1}{R}_p{L}_s+⟨i_{L_p}{⟩}_1^I\omega +⟨u_{C_p}{⟩}_1^R{\lambda }^{-1}{L}_s+⟨u_{C_p}{⟩}_1^{I}0+⟨i_{L_s}{⟩}_1^R{\lambda }^{-1}M{R}_s+⟨i_{L_s}{⟩}_1^{I}0+⟨u_{C_s}{⟩}_1^R{\lambda }^{-1}M+⟨u_{C_s}{⟩}_1^{I}0+⟨u_{C_f}{⟩}_0{\lambda }^{-1}M⟨S_r{⟩}_1^R\\ \frac{d⟨i_{L_p}{⟩}_1^I}{dt}& ={\lambda }^{-1}\left(R_p{L}_s⟨i_{L_p}{⟩}_1^I+L_s⟨u_{C_p}{⟩}_1^I+M{R}_s⟨i_{L_s}{⟩}_1^I+M⟨u_{C_s}{⟩}_1^I+M⟨S_r{u}_{C_f}{⟩}_1^I-L_s{U}_{\mathrm{in}}⟨S_i{⟩}_1^I\right)-\omega ⟨i_{L_p}{⟩}_1^R\\ & ={\lambda }^{-1}\left(R_p{L}_s⟨i_{L_p}{⟩}_1^I+L_s⟨u_{C_p}{⟩}_1^I+M{R}_s⟨i_{L_s}{⟩}_1^I+M⟨u_{C_s}{⟩}_1^I+M(⟨S_r{⟩}_0⟨u_{C_f}{⟩}_1^I+⟨S_r{⟩}_1^I⟨u_{C_f}{⟩}_0)-L_s{U}_{\mathrm{in}}⟨S_i{⟩}_1^I\right)-\omega ⟨i_{L_p}{⟩}_1^R\end{array}$$

• $⟨S_i{⟩}_0=0,⟨S_i{⟩}_1^R=0,⟨S_i{⟩}_1^I=\frac{2}{\pi }$
• $⟨S_r{⟩}_0=0,⟨S_r{⟩}_1^R=\frac{2}{\pi },⟨S_i{⟩}_1^I=0$

State space model:
$$\{\begin{array}{l}\dot{\mathbf{x}}=\mathbf{A}\cdot \mathbf{x}+\mathbf{B}\cdot U_{\mathrm{in}}\\ y={⟨u_{C_f}⟩}_0\end{array}$$
where
$$\begin{array}{rl}\mathbf{x}& ={\left[⟨i_{L_p}{⟩}_1^R,⟨i_{L_p}{⟩}_1^I,⟨u_{C_p}{⟩}_1^R,⟨u_{C_p}{⟩}_1^I,⟨i_{L_s}{⟩}_1^R,⟨i_{L_s}{⟩}_1^I,⟨u_{C_s}{⟩}_1^R,⟨u_{C_s}{⟩}_1^I,⟨u_{C_f}{⟩}_0\right]}^T\\ \mathbf{A}& =\left[\begin{array}{ccccccccc}{R}_p{L}_s\frac{1}{\lambda }& \omega & L_s\frac{1}{\lambda }& 0& M{R}_s\frac{1}{\lambda }& 0& M\frac{1}{\lambda }& 0& 2\frac{1}{\pi }M\frac{1}{\lambda }\\ -\omega & R_p{L}_s\frac{1}{\lambda }& 0& L_s\frac{1}{\lambda }& 0& M{R}_s\frac{1}{\lambda }& 0& M\frac{1}{\lambda }& 0\\ C_p^{-1}& 0& 0& \omega & 0& 0& 0& 0& 0\\ 0& C_p^{-1}& -\omega & 0& 0& 0& 0& 0& 0\\ M{R}_p\frac{1}{\lambda }& 0& M\frac{1}{\lambda }& 0& R_s{L}_p\frac{1}{\lambda }& \omega & L_p\frac{1}{\lambda }& 0& 2\frac{1}{\pi }{L}_p\frac{1}{\lambda }\\ 0& M{R}_p\frac{1}{\lambda }& 0& M\frac{1}{\lambda }& -\omega & R_s{L}_p\frac{1}{\lambda }& 0& L_p\frac{1}{\lambda }& 0\\ 0& 0& 0& 0& C_s^{-1}& 0& 0& \omega & 0\\ 0& 0& 0& 0& 0& C_s^{-1}& -\omega & 0& 0\\ 0& 0& 0& 0& 4\frac{1}{\pi }{C}_f^{-1}& 0& 0& 0& -C_f^{-1}{R}_{\mathrm{dc}}^{-1}\end{array}\right]\\ \mathbf{B}& ={\left[\begin{array}{lllllllll}0& 2\frac{1}{\pi }{L}_s\frac{1}{\lambda }& 0& 0& 0& 2\frac{1}{\pi }M\frac{1}{\lambda }& 0& 0& 0\end{array}\right]}^T\end{array}$$

• $\lambda =M^2-L_s{L}_p$

Simulation study

Configuration

SIMULINK 2018a or higher
仿真使用了移相控制，占空比 0.7，本文中的模型没有考虑移相控制，或者可以认为本文的模型是开关管满开的状态，即占空比为1，感兴趣的同学可以自己推导一下，后面有时间我可能会补上详细的推导。

Matlab code:

%---------------------------------------
% This is the simulation from yangHierarchical2018 
% Hierarchical multiobjective H-infinity robust control
% design for wireless power transfer system using genetic algorithm
%
%
% hu 2023-03-08 Created
% hu 2023-03-19 Corrected one error in the paper 
% hu 2023-04-05 Corrected one error in the paper 
% hu 2023-04-10 Applied ODE45 to solve ODE
% hu 2023-05-23 Dual direction phase shift is included and verified
%---------------------------------------

clc,clear,close all



ts = 0;
tf = .05;

Vin = 100;
%                 [iL1; uC1; iL2; uC2; vo];
flagModOutput   = [ 1;   1;   1;   1;   1]; 
flagSimOutput   = flagModOutput;
flagInterpertor = 1; % First order interper for Modelled signals


Rdc = 15;
f   = 85e3;
T   = 1 / f;
fC  = @(L)(1/2/pi/f)^2/L;
fw  = @(L,C)1/2/pi/sqrt(L * C);

Cf  = 4700e-6;
L1  = 275e-6;
L2  = 275e-6;
C1  = 12.75e-9;
C2  = 12.70e-9;
R2  = .191;
R1  = .192;
M   = 91.5e-6;
k12 = M / sqrt(L2 * L1);
u   = 100;
D   = .7; % Duty which is in 0 to 1;
Phaseshift = D;


lambda = M^2 - L1 * L2;
w      = 2 * pi * f;

f1 = fw(L1,C1);
f2 = fw(L2,C2);


Sr1R = sin(pi / 2 * D) * 2 / pi;
Si1I = sin(pi / 2 * D) * 2 / pi;

p1 = R1 * L2 * lambda^-1;
p2 = L2 * lambda^-1;
p3 = M  * R2 * lambda^-1; 
p4 = M  * lambda^-1;
p5 = Sr1R * M * lambda^-1;
s1 = M  * R1 * lambda^-1;
s2 = M  * lambda^-1;
s3 = R2 * L1 * lambda^-1;
s4 = L1 * lambda^-1;
s5 = Sr1R * L1 * lambda^-1;
c1 = 4 / pi / Cf;
c2 = -1 / Cf / Rdc;
b1 = Si1I * L2 / lambda;
b2 = Si1I * M / lambda;
% ----------------------------
% ----  Consider Cf ----
% ----------------------------

A(1,:) = [p1,   w,    p2,   0,    p3, 0,  p4, 0,  p5];
A(2,:) = [-w,   p1,   0,    p2,   0,  p3, 0,  p4, 0 ];
A(3,:) = [1/C1, 0,    0,    w,    zeros(1,5)];
A(4,:) = [0,    1/C1, -w,   0,    zeros(1,5)];
A(5,:) = [s1,   0,    s2,   0,    s3, w,  s4, 0,  s5];
A(6,:) = [0,    s1,   0,    s2,   -w, s3, 0,  s4, 0 ];
A(7,:) = [zeros(1,4), 1/C2, 0,    0,  w, 0];
A(8,:) = [zeros(1,4), 0,    1/C2, -w, 0, 0 ];
A(9,:) = [zeros(1,4), c1, 0,   0,  0, c2];

B = [0, b1, 0, 0, 0, b2, 0, 0, 0]';

A
B


tspan  = [ts,tf];
Relerr = 1e-7; % Relative error bound
Abserr = 1e-6; % Absolute error bound
x0     = zeros(9,1);
xdot   = @(t,x)A * x + B * u;
options = odeset('RelTol',Relerr,'AbsTol',Abserr,'Stats','on');
[t,x] =ode45(@(t,x)A * x + B * u,tspan,x0,options);

if(flagModOutput(1)) iL1out  = 2 * x(:,1) .* cos(w * t) - 2 * x(:,2) .* sin(w * t); end
if(flagModOutput(2)) uC1out  = 2 * x(:,3) .* cos(w * t) - 2 * x(:,4) .* sin(w * t); end
if(flagModOutput(3)) iL2out  = 2 * x(:,5) .* cos(w * t) - 2 * x(:,6) .* sin(w * t); end
if(flagModOutput(4)) uC2out  = 2 * x(:,7) .* cos(w * t) - 2 * x(:,8) .* sin(w * t); end
if(flagModOutput(5)) voout   = x(:,9); end

global ii, ii = 0;

%%

sim WPTWithPhaseShiftControl;
SIM = ans;

if(flagSimOutput(2)) uC1outSIM = SIM.SimData.Data(:,1); end
if(flagSimOutput(1)) iL1outSIM = SIM.SimData.Data(:,2); end
if(flagSimOutput(4)) uC2outSIM = SIM.SimData.Data(:,3); end
if(flagSimOutput(3)) iL2outSIM = SIM.SimData.Data(:,4); end
if(flagSimOutput(5)) vooutSIM  = SIM.SimData.Data(:,5); end

toutSIM   = SIM.tout;

if(flagInterpertor)
    if(flagSimOutput(1)) iL1out = interp1(t,iL1out,toutSIM); end
    if(flagSimOutput(2)) uC1out = interp1(t,uC1out,toutSIM); end
    if(flagSimOutput(3)) iL2out = interp1(t,iL2out,toutSIM); end
    if(flagSimOutput(4)) uC2out = interp1(t,uC2out,toutSIM); end
    if(flagSimOutput(5)) voout  = interp1(t,voout,toutSIM);  end
end


close all


pos = mypos(8);
i   = 1;
linewidth = 1.5;
fontsize  = 12;

tsplot    = 0;
tfplot    = tf - T;
M1        = find(toutSIM>tsplot,1);
M2        = find(toutSIM>tfplot,1);
xlim      = [tsplot,tfplot];
toutSIMplot   = toutSIM(M1:M2,1);
iL1outSIMplot = iL1outSIM(M1:M2,1);
uC1outSIMplot = uC1outSIM(M1:M2,1);
iL2outSIMplot = iL2outSIM(M1:M2,1);
uC2outSIMplot = uC2outSIM(M1:M2,1);
vooutSIMplot  = vooutSIM(M1:M2,1);

iL1outplot = iL1out(M1:M2,1);
uC1outplot = uC1out(M1:M2,1);
iL2outplot = iL2out(M1:M2,1);
uC2outplot = uC2out(M1:M2,1);
vooutplot  = voout(M1:M2,1);

if(flagModOutput(1))
    figure
    plot(toutSIMplot,iL1outplot,toutSIMplot,iL1outSIMplot,'linewidth',linewidth);
    set(gca,'XLim',xlim);
    h = legend('$i_{L1_{GSSA}}$','$i_{L1_{SIM}}$');
    h.Interpreter = 'latex';
    h.FontSize    = fontsize;
    h.Location    = 'northeast';
    h.Orientation = 'horizon';
    set(gcf,'position',pos{i});
    i = i + 1;
    grid on
end

if(flagModOutput(2))
    figure
    plot(toutSIMplot,uC1outplot,toutSIMplot,uC1outSIMplot,'linewidth',linewidth);
    set(gca,'XLim',xlim);
    h = legend('$u_{C1_{GSSA}}$', '$u_{C1_{SIM}}$');
    h.Interpreter = 'latex';
    h.FontSize    = fontsize;
    h.Location    = 'northeast';
    h.Orientation = 'horizon';
    set(gcf,'position',pos{i});
    i = i + 1;
    grid on
end

if(flagModOutput(3))
    figure
    plot(toutSIMplot,iL2outplot,toutSIMplot,iL2outSIMplot,'linewidth',linewidth);
    set(gca,'XLim',xlim);
    h = legend('$i_{L2_{GSSA}}$','$i_{L2_{SIM}}$');
    h.Interpreter = 'latex';
    h.FontSize    = fontsize;
    h.Location    = 'northeast';
    h.Orientation = 'horizon';
    set(gcf,'position',pos{i});
    i = i + 1;
    grid on
end

if(flagModOutput(4))
    figure
    plot(toutSIMplot,uC2outplot,toutSIMplot,uC2outSIMplot,'linewidth',linewidth);
    set(gca,'XLim',xlim);
    h = legend('$u_{C2_{GSSA}}$', '$u_{C2_{SIM}}$');
    h.Interpreter = 'latex';
    h.FontSize    = fontsize;
    h.Location    = 'northeast';
    h.Orientation = 'horizon';
    set(gcf,'position',pos{i});
    i = i + 1;
    grid on
end

if(flagModOutput(5))
    figure
    plot(toutSIMplot,vooutplot,toutSIMplot,vooutSIMplot,'linewidth',linewidth);
    set(gca,'XLim',xlim);
    h = legend('$u_{o_{GSSA}}$', '$u_{o_{SIM}}$');
    h.Interpreter = 'latex';
    h.FontSize    = fontsize;
    h.Location    = 'southeast';
    h.Orientation = 'horizon';
    set(gcf,'position',pos{i});
    i = i + 1;
    grid on
end

mypos function:

function pos = mypos(i,figs1,figs2)
% mypos.m                    给定 figure 对象个数求解合适的摆放位置向量以防止图片堆叠
% i                          figure 个数(直接写8就好了，用不到的就放着呗)
% figs1,figs2                figure 对象的长和高
% pos = mypos(i,figs1,figs2) 求出 i 个 figure 对象的合理摆放位置，且大小设置为[figs1,figs2]
%                            输出 pos 是元胞数组，使用规范（已生成figure对象后）：set(gcf,'position',pos{i})
% Remark                     更方便的绘图程序见 myplot.m

% hu 2018-6-11
% hu 2018-8-8  Modified Remark is added
% hu 2018-11-3 Modified Description is updated

if nargin ~= 3
	figs = [400,300]; %default size is 560*420, 500*280 is suitable for paper shows
else
    figs = [figs1,figs2];
end
if i > 8
    disp('too many figures! The maximum number is 8')
end
scr = get(0,'screensize');
for k = 1:i
    if k <= 4
        pos{k} = [scr(1) + (k - 1) * figs(1),scr(2) + scr(4) / 2,figs];
    end
    if k > 4
        pos{k} = [scr(1) + (k - 5) * scr(3) / 4,scr(2) + 30,figs];
    end
end
end

Results

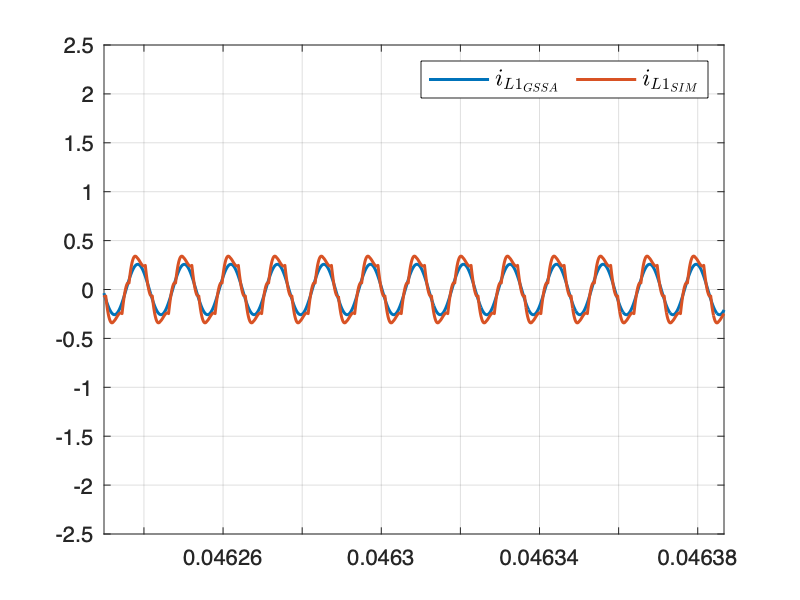
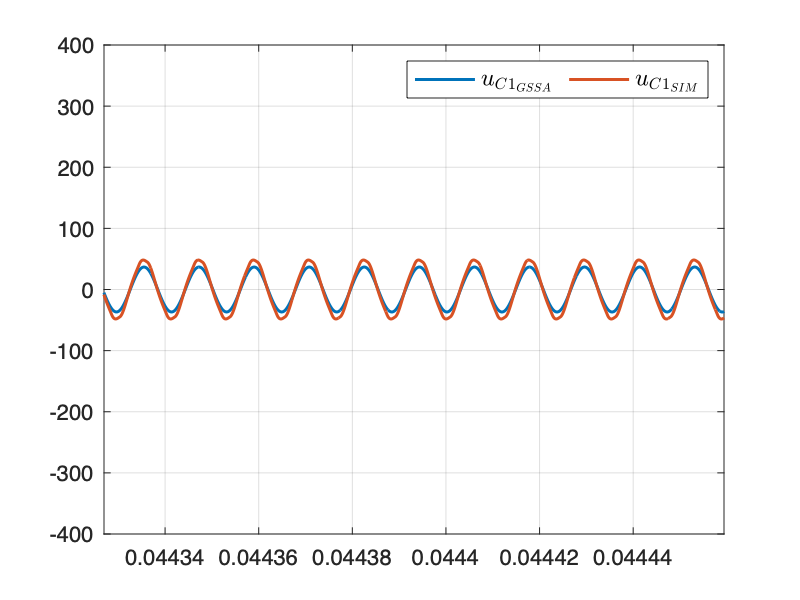
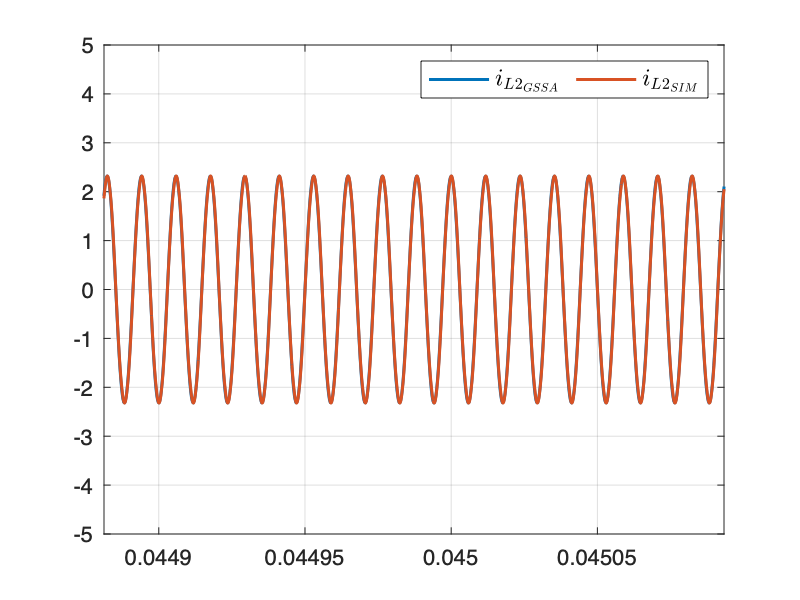
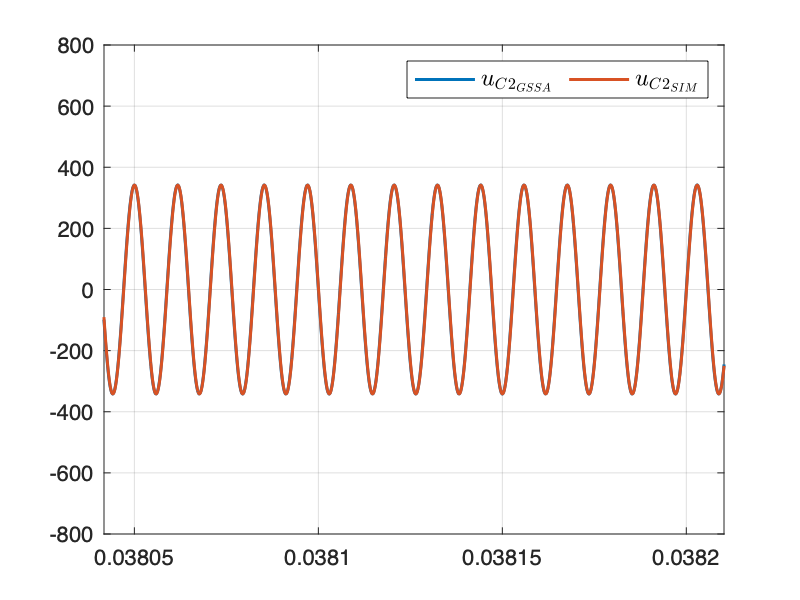
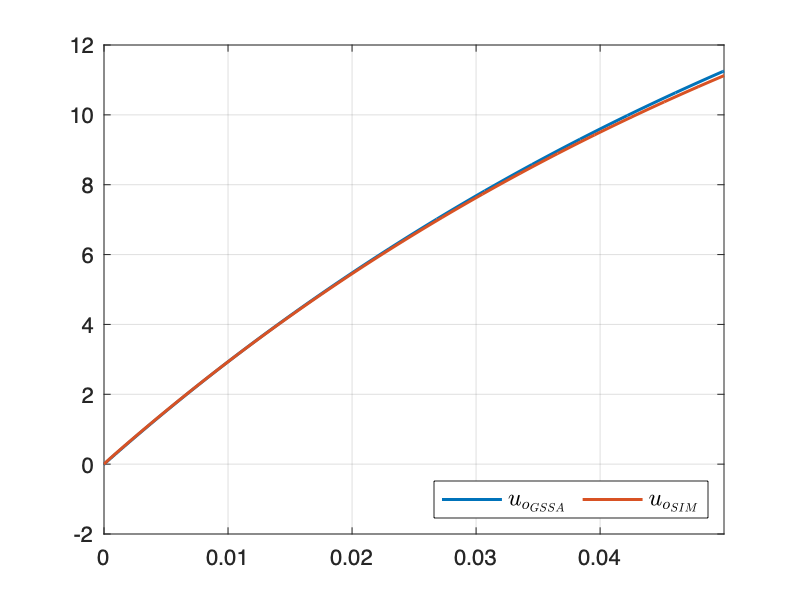
仿真结果与 SIMULINK 模型几乎重合，验证了建模的正确性

仿真模型：

https://download.csdn.net/download/hu3350261/87812337