9. 概率图模型
9.1 背景介绍
9.1.1 概述
- 什么是概率图
- 机器学习的重要思想就是,对已有的数据进行分析,然后对未知数据来进行预判或者预测等。概率图是将
概
率
的
特
征
引
入
到
图
中
\color{blue}概率的特征引入到图中
概率的特征引入到图中,方便进行直观分析,即:
有
图
有
真
相
\color{red}有图有真相
有图有真相。
- 概 率 \color{red}概率 概率:指概率模型,在机器学习中是对新的数据进行一些预测,对已知数据做聚类等。总的来说,就是对已有数据做一些操作,来预测未来。
- 图 \color{red}图 图:与数据结构的图一样,有无向图、有向图等。与数据结构不同的是,将概率嵌入图中,使得模型更加直观,可以将概率模型的特征明显表示出来。
- 由于现实世界的复杂性,数据通常都是多维的,因此以下用高维随机变量来讨论。
- 机器学习的重要思想就是,对已有的数据进行分析,然后对未知数据来进行预判或者预测等。概率图是将
概
率
的
特
征
引
入
到
图
中
\color{blue}概率的特征引入到图中
概率的特征引入到图中,方便进行直观分析,即:
有
图
有
真
相
\color{red}有图有真相
有图有真相。
- 高维随机变量性质
- 假设有一组高维随机变量,
p
(
x
1
,
x
2
,
⋯
,
x
n
)
p(x_1,x_2,\cdots,x_n)
p(x1,x2,⋯,xn),它有两个基本的概率定义:条件概率和边缘概率。条件概率的描述为
p
(
x
i
)
p(x_i)
p(xi),条件概率的描述为
p
(
x
j
∣
x
i
)
p(x_j|x_i)
p(xj∣xi)。根据这两个基本的概率,可得基本的运算法则:则:
- Sum Rule: p ( x 1 ) = ∫ p ( x 1 , x 2 ) d x 2 . (9.1.1) p(x_{1})=\int p(x_{1},x_{2})\mathrm{d}x_{2}.\tag{9.1.1} p(x1)=∫p(x1,x2)dx2.(9.1.1)
- Product Rule: p ( x 1 , x 2 ) = p ( x 1 ∣ x 2 ) p ( x 2 ) . (9.1.2) p(x_{1},x_{2})=p(x_{1}|x_{2})p(x_{2}).\tag{9.1.2} p(x1,x2)=p(x1∣x2)p(x2).(9.1.2)
- Chain Rule: p ( x 1 , x 2 , ⋯ , x p ) = ∏ i = 1 p p ( x i ∣ x i + 1 , x i + 2 , ⋯ , x p ) . (9.1.3) p(x_{1},x_{2},\cdots ,x_{p})=\prod_{i=1}^{p}p(x_{i}|x_{i+1},x_{i+2},\cdots ,x_{p}).\tag{9.1.3} p(x1,x2,⋯,xp)=i=1∏pp(xi∣xi+1,xi+2,⋯,xp).(9.1.3)
- Bayesian Rule: P ( x 2 ∣ x 1 ) = P ( x 1 , x 2 ) P ( x 1 ) = P ( x 1 , x 2 ) ∫ P ( x 1 , x 2 ) d x 2 = P ( x 2 ) P ( x 1 ∣ x 2 ) ∫ P ( x 2 ) P ( x 1 ∣ x 2 ) d x 2 . (9.1.4) P(x_{2}|x_{1})=\frac{P(x_{1},x_{2})}{P(x_{1})}=\frac{P(x_{1},x_{2})}{\int P(x_{1},x_{2})\mathrm{d}x_{2}}=\frac{P(x_{2})P(x_{1}|x_{2})}{\int P(x_{2})P(x_{1}|x_{2})\mathrm{d}x_{2}}.\tag{9.1.4} P(x2∣x1)=P(x1)P(x1,x2)=∫P(x1,x2)dx2P(x1,x2)=∫P(x2)P(x1∣x2)dx2P(x2)P(x1∣x2).(9.1.4)
- 高维随机变量困境:维度高,计算复杂,联合概率使用链式法则计算量太大。
当维度较高时, p ( x 1 , x 2 , ⋯ , x N ) = ∏ i = 1 N p ( x i ∣ x 1 , x 2 , ⋯ , x i − 1 ) p(x_1,x_2,\cdots,x_N) = \prod_{i=1}^N p(x_i|x_1,x_2,\cdots,x_{i-1}) p(x1,x2,⋯,xN)=∏i=1Np(xi∣x1,x2,⋯,xi−1)会算炸,因此需要简化运算。
- 假设有一组高维随机变量,
p
(
x
1
,
x
2
,
⋯
,
x
n
)
p(x_1,x_2,\cdots,x_n)
p(x1,x2,⋯,xn),它有两个基本的概率定义:条件概率和边缘概率。条件概率的描述为
p
(
x
i
)
p(x_i)
p(xi),条件概率的描述为
p
(
x
j
∣
x
i
)
p(x_j|x_i)
p(xj∣xi)。根据这两个基本的概率,可得基本的运算法则:则:
9.1.2 简化模型和算法分类
- 由于高位随机变量计算复杂度高,需要简化运算,介绍简化思路:
- 相互独立的假设
P ( x 1 , x 2 , ⋯ , x p ) = ∏ i = 1 p P ( x i ) . (9.1.5) P(x_{1},x_{2},\cdots ,x_{p})=\prod_{i=1}^{p}P(x_{i}).\tag{9.1.5} P(x1,x2,⋯,xp)=i=1∏pP(xi).(9.1.5)
也可以称为:朴素贝叶斯中的条件独立性假设( P ( x ∣ y ) = ∏ i = 1 p P ( x i ∣ y ) P(x|y)=\prod_{i=1}^{p}P(x_{i}|y) P(x∣y)=∏i=1pP(xi∣y));这个假设太强,实际情况中的依赖比这个要复杂的多。所以放弱一点,增加之间的依赖关系。 -
M
a
r
k
o
v
P
r
o
p
e
r
t
y
\color{red}Markov\; Property
MarkovProperty
马尔可夫性质:对于一个序列 { x 1 , x 2 , ⋯ , x N } \{ x_1,x_2,\cdots,x_N \} {x1,x2,⋯,xN},第 i i i项仅仅只和第 i − 1 i-1 i−1项之间存在依赖关系。用符号的方法我们可以表示为:
x j ⊥ x i + 1 ∣ x i , j < i . (9.1.6) x_{j}\perp x_{i+1}| x_{i},j< i.\tag{9.1.6} xj⊥xi+1∣xi,j<i.(9.1.6)
在HMM里面就是齐次Markov假设,但是还是太强了,我们还是要想办法削弱。 -
条
件
独
立
性
假
设
{\color{Red}{条件独立性假设}}
条件独立性假设
条件独立性假设是概率图的核心概念,可以大大的简化联合概率分布。而用图可以可视化表达条件独立性,用公式可以描述为:
x A ⊥ x B ∣ x C . (9.1.7) \color{red}x_{A}\perp x_{B}|x_{C}.\tag{9.1.7} xA⊥xB∣xC.(9.1.7)
x A 、 x B 、 x C x_{A}、x_{B}、x_{C} xA、xB、xC是 集 合 , 且 不 相 交 \color{blue}集合,且不相交 集合,且不相交。
- 相互独立的假设
- 概率图算法分类
概率图的算法大致可以分为三类:表示(Representation),推断(Inference)和学习(Learning),如下图:
概 率 图 { R e p r e s e n t a t i o n ( 表 示 ) { 有 向 图 B e y e s i a n N e t w o r k 高 斯 图 ( 连 续 ) { G a u s s i a n B N G a u s s i a n M N 无 向 图 M a r k o v N e t w o r k I n f e r e n c e ( 推 断 ) { 精 确 推 断 近 似 推 断 { 确 定 性 近 似 ( 变 分 推 断 ) 随 机 近 似 ( M C M C ) L e a r n i n g ( 学 习 ) { 参 数 学 习 { 完 备 数 据 { 有 向 无 向 隐 变 量 → E M 结 构 学 习 (9.1.8) \color{blue}概率图\left\{\begin{matrix} Representation(表示)\left\{\begin{matrix} 有向图\; Beyesian\; Network\\ 高斯图(连续)\left\{\begin{matrix} Gaussian\; BN\\ Gaussian\; MN \end{matrix}\right.\\ 无向图\; Markov\; Network \end{matrix}\right.\\ Inference(推断)\left\{\begin{matrix} 精确推断\\ 近似推断\left\{\begin{matrix} 确定性近似(变分推断)\\ 随机近似(MCMC) \end{matrix}\right. \end{matrix}\right.\\ Learning(学习)\left\{\begin{matrix} 参数学习\left\{\begin{matrix} 完备数据\left\{\begin{matrix} 有向\\ 无向 \end{matrix}\right.\\ 隐变量\rightarrow EM \end{matrix}\right.\\ 结构学习 \end{matrix}\right. \end{matrix}\right.\tag{9.1.8} 概率图⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧Representation(表示)⎩⎪⎪⎨⎪⎪⎧有向图BeyesianNetwork高斯图(连续){GaussianBNGaussianMN无向图MarkovNetworkInference(推断)⎩⎨⎧精确推断近似推断{确定性近似(变分推断)随机近似(MCMC)Learning(学习)⎩⎪⎪⎨⎪⎪⎧参数学习⎩⎨⎧完备数据{有向无向隐变量→EM结构学习(9.1.8)- 表 示 \color{blue}表示 表示的方法可以分为有向图,Bayesian Network;和无向图,Markov Network,这两种图通常用来处理变量离散的情况。对于连续性的变量,我们通常采用高斯图,同时可以衍生出,Gaussian Bayesian Network和Guassian Markov Network。
- 推 断 \color{blue}推断 推断可以分为精准推断和近似推断。所谓推断就是给定已知求概率分布。近似推断中可以分为确定性推断(变分推断)和随机推断(MCMC),MCMC是基于蒙特卡罗采样的。
- 学 习 \color{blue}学习 学习可以分为参数学习和结构学习。在参数学习中,参数可分为完备数据和非隐数据,我们可以采用有向图或者无向图来解决。而隐变量的求解我们需要使用到EM算法(EM算法在后面的章节会详细推导)。而结构学习则是,需要我们知道使用那种图结构更好,比如神经网络中的节点个数,层数等等,也就是现在非常热的Automate Machine Learning。
9.2 贝叶斯网络-Representation-条件独立性
9.2.1 概述
- 回顾
上一节我们知道高维随机变量的链式法则:
p ( x 1 , x 2 , ⋯ , x p ) = ∏ i = 1 p p ( x i ∣ x i + 1 , x i + 2 , ⋯ , x p ) p(x_{1},x_{2},\cdots ,x_{p})=\prod_{i=1}^{p}p(x_{i}|x_{i+1},x_{i+2},\cdots ,x_{p}) p(x1,x2,⋯,xp)=i=1∏pp(xi∣xi+1,xi+2,⋯,xp)
由于计算维度太高了,因此引入条件独立性,表达为 X A ⊥ X B ∣ X C X_A\bot X_B | X_C XA⊥XB∣XC( X A 、 X B 、 X C X_{A}、X_{B}、X_{C} XA、XB、XC是 集 合 , 且 不 相 交 \color{blue}集合,且不相交 集合,且不相交)。采用 因 子 分 解 \color{red}因子分解 因子分解的方法我们将联合概率的计算进行分解为:
p ( x 1 , x 2 , ⋯ , x N ) = ∏ i = 1 N p ( x i ∣ x p a { i } ) . (9.2.1) p(x_1,x_2,\cdots,x_N)=\prod_{i=1}^Np(x_i|x_{pa\{i\}}).\tag{9.2.1} p(x1,x2,⋯,xN)=i=1∏Np(xi∣xpa{i}).(9.2.1)
其中, p a { i } pa\{i\} pa{i}表示为 x i x_i xi的父亲节点。 - 拓扑排序
因 子 分 解 \color{red}因子分解 因子分解采用概率图表示条件独立性,直观性强。核心思想: 拓 扑 排 序 \color{red}拓扑排序 拓扑排序。如果存在一个关系由一个节点 x i x_i xi指向另一个节点 x j x_j xj,我们可以记为 p ( x j ∣ x i ) p(x_j|x_i) p(xj∣xi),如下图所示:

对于一个箭头 ⟶ \longrightarrow ⟶来说,箭头所在的方向称为Head,另一端被称为Tail。构建出概率图以后,我们可以根据图写出因子分解的结果。
9.2.2 概率图的三种基本结构
- 在局部的任何三个节点,可以有以下三种结构:
- Tail to Tail
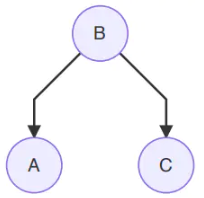
- 性质:
这种结构满足:
A ⊥ C ∣ B ⇔ 若 B 被 观 测 , 则 路 径 被 阻 塞 , A 与 C 独 立 。 (9.2.2) \color{red}A\perp C|B\Leftrightarrow 若B被观测,则路径被阻塞,A与C独立。\tag{9.2.2} A⊥C∣B⇔若B被观测,则路径被阻塞,A与C独立。(9.2.2) - 证明:
通过因子分解和链式规则可以进行证明:
P ( A , B , C ) = P ( A ∣ B ) P ( B ) P ( C ∣ B ) ⏟ 因 子 分 解 = P ( B ) P ( A ∣ B ) P ( C ∣ A , B ) ⏟ 链 式 法 则 ⇒ P ( C ∣ B ) = P ( C ∣ A , B ) ⇒ P ( C ∣ B ) P ( A ∣ B ) = P ( C ∣ A , B ) P ( C ∣ B ) ⇒ P ( C ∣ B ) P ( A ∣ B ) = P ( A , C ∣ B ) ⇒ C ⊥ A ∣ B P(A,B,C)=\underset{因子分解}{\underbrace{P(A|B)P(B)P(C|B)}}=\underset{链式法则}{\underbrace{P(B)P(A|B)P(C|A,B)}}\\ \Rightarrow P(C|B)=P(C|A,B)\\ \Rightarrow P(C|B)P(A|B)=P(C|A,B)P(C|B)\\ \Rightarrow P(C|B)P(A|B)=P(A,C|B)\\ \Rightarrow C\perp A|B P(A,B,C)=因子分解 P(A∣B)P(B)P(C∣B)=链式法则 P(B)P(A∣B)P(C∣A,B)⇒P(C∣B)=P(C∣A,B)⇒P(C∣B)P(A∣B)=P(C∣A,B)P(C∣B)⇒P(C∣B)P(A∣B)=P(A,C∣B)⇒C⊥A∣B
这就是条件独立性,在B已知的条件下,A和C独立。概率图中就已经蕴含这个分解了,只看图就可以看到这个性质,这就是图的直观性,条件独立性和图是一样的。
- 性质:
- Head to Head

- 性质
这种结构满足:
默 认 情 况 下 , A ⊥ C , 路 径 是 阻 塞 的 , A 与 C 独 立 。 { 若 B 被 观 测 , 则 路 径 是 通 , A 与 C 不 独 立 ; 若 B 仍 有 后 继 节 点 , 若 后 继 节 点 被 观 测 , 路 径 也 通 。 (9.2.3) \color{red}默认情况下,A\perp C,路径是阻塞的,A与C独立。\\\left\{\begin{matrix} 若B被观测,则路径是通,A与C不独立;\\若B仍有后继节点,若后继节点被观测,路径也通。\end{matrix}\right.\tag{9.2.3} 默认情况下,A⊥C,路径是阻塞的,A与C独立。{若B被观测,则路径是通,A与C不独立;若B仍有后继节点,若后继节点被观测,路径也通。(9.2.3)
如 果 B 有 孩 子 B ∗ , B ∗ ∗ , 那 么 B 的 孩 子 依 然 有 B 的 性 质 \color{red}如果B有孩子B^*, B^{**},那么B的孩子依然有B的性质 如果B有孩子B∗,B∗∗,那么B的孩子依然有B的性质。 - 证明
通过因子分解和链式规则可以进行证明:
P ( A , B , C ) = P ( A ) P ( C ) P ( B ∣ A , C ) ⏟ 因 子 分 解 = P ( A ) P ( C ∣ A ) P ( B ∣ A , C ) ⏟ 链 式 法 则 ⇒ P ( C ) = P ( C ∣ A ) ⇒ A ⊥ C P(A,B,C)=\underset{因子分解}{\underbrace{P(A)P(C)P(B|A,C)}}=\underset{链式法则}{\underbrace{P(A)P(C|A)P(B|A,C)}}\\ \Rightarrow P(C)=P(C|A)\\ \Rightarrow A\perp C P(A,B,C)=因子分解 P(A)P(C)P(B∣A,C)=链式法则 P(A)P(C∣A)P(B∣A,C)⇒P(C)=P(C∣A)⇒A⊥C
- 性质
- Head to Tail

- 性质
这种结构满足:
A ⊥ C ∣ B ⇔ 若 B 被 观 测 , 则 路 径 被 阻 塞 , A 与 C 独 立 。 (9.2.4) \color{red}A\perp C|B\Leftrightarrow 若B被观测,则路径被阻塞,A与C独立。\tag{9.2.4} A⊥C∣B⇔若B被观测,则路径被阻塞,A与C独立。(9.2.4) - 证明
通过因子分解和链式规则可以进行证明:
P ( A , B , C ) = P ( A ) P ( B ∣ A ) P ( C ∣ B ) ⏟ 因 子 分 解 = P ( A ) P ( B ∣ A ) P ( C ∣ B , A ) ⏟ 链 式 法 则 ⇒ P ( C ∣ B ) = P ( C ∣ B , A ) ⇒ P ( C ∣ B ) P ( A ∣ B ) = P ( C ∣ A , B ) P ( A ∣ B ) ⇒ P ( C ∣ B ) P ( A ∣ B ) = P ( C , A ∣ B ) ⇒ C ⊥ A ∣ B P(A,B,C)=\underset{因子分解}{\underbrace{P(A)P(B|A)P(C|B)}}=\underset{链式法则}{\underbrace{P(A)P(B|A)P(C|B,A)}}\\ \Rightarrow P(C|B)=P(C|B,A)\\ \Rightarrow P(C|B)P(A|B)=P(C|A,B)P(A|B)\\ \Rightarrow P(C|B)P(A|B)=P(C,A|B)\\ \Rightarrow C\perp A|B P(A,B,C)=因子分解 P(A)P(B∣A)P(C∣B)=链式法则 P(A)P(B∣A)P(C∣B,A)⇒P(C∣B)=P(C∣B,A)⇒P(C∣B)P(A∣B)=P(C∣A,B)P(A∣B)⇒P(C∣B)P(A∣B)=P(C,A∣B)⇒C⊥A∣B
- 性质
- Tail to Tail
9.3 贝叶斯网络-Representation-D-Seperation
在概率图中,我们用:
- p ( x 1 , x 2 , ⋯ , x N ) = ∏ i = 1 N p ( x i ∣ x p a { i } ) p(x_1,x_2,\cdots,x_N)=\prod_{i=1}^Np(x_i|x_{pa\{i\}}) p(x1,x2,⋯,xN)=∏i=1Np(xi∣xpa{i})
-
p
(
x
1
,
x
2
,
⋯
,
x
N
)
=
p
(
x
i
)
∏
i
=
1
N
p
(
x
i
∣
x
1
:
i
−
1
)
p(x_1,x_2,\cdots,x_N)=p(x_i)\prod_{i=1}^Np(x_i|x_{1:i-1})
p(x1,x2,⋯,xN)=p(xi)∏i=1Np(xi∣x1:i−1)
这两种表达形式是等价的。式子2是最完备的表达方法,式子1是表达是简化版本,他蕴含了概率图中得到的条件独立性关系简化的结果。我们通过D-Separation和Markov Blanket对上面两式子进行更深层次的理解:- D-Separation是在概率图中,帮助我们快速的判断条件独立性。
- 对于一个节点,它和哪些节点相关,它和和父亲,孩子,孩子的另一个双亲这三种节点相关,这三种点的集合就是Markov Blanket。
9.3.1 D-separation
有三个集合
X
A
,
X
B
,
X
C
X_A,X_B,X_C
XA,XB,XC,并且满足
X
A
⊥
X
C
∣
X
B
X_A\bot X_C|X_B
XA⊥XC∣XB。有一些节点连成的拓扑关系图,其中的节点
a
∈
X
A
,
c
∈
X
C
a\in X_A,c\in X_C
a∈XA,c∈XC,想要
a
a
a和
c
c
c之间相互独立,他们之间连接的节点需要满足什么样的条件才能满足D-Seperation?

假如从
a
a
a到
c
c
c中间通过一个节点
b
b
b,那么路径什么时候是连通的?什么时候又是阻塞的呢?
-
H
e
a
d
t
o
T
a
i
l
\color{green}Head\;to\;Tail
HeadtoTail
如图中绿色所示, a a a到 c c c中间的节点 b 1 b_1 b1,那么 b 1 b_1 b1必须被观测到( b 1 ∈ X B \color{green}b_1\in X_B b1∈XB), a a a与 c c c之间才能独立。 -
T
a
i
l
t
o
T
a
i
l
\color{red}Tail\;to\;Tail
TailtoTail
如图中红色所示, a a a到 c c c中间的节点 b 2 b_2 b2,那么 b 2 b_2 b2必须被观测到( b 2 ∈ X B \color{red}b_2\in X_B b2∈XB), a a a与 c c c之间才能独立。 -
H
e
a
d
t
o
H
e
a
d
\color{black}Head\;to\;Head
HeadtoHead
如图中黑色所示, a a a到 c c c中间的节点 b ∗ b^* b∗(以及 b b b的孩子 b ∗ , b ∗ ∗ b^*, b^{**} b∗,b∗∗) ,那么 b ∗ b^* b∗及其孩子必须不被观测到( b ∗ , b ∗ , b ∗ ∗ ∉ X B \color{black}b^*,b^*, b^{**}\notin X_B b∗,b∗,b∗∗∈/XB), a a a与 c c c之间才能独立。
符合上述3条规则,那么我们就可以称 a a a和 c c c之间是D-Separation的,也叫做全局马尔科夫性质 (Global Markov Property)。D-Separation非常的关键,我们可以直接用这个性质来检测两个集合关于另外一个集合被观测的条件是不是条件独立。
9.3.2 马尔可夫毯(Markov Blanket)
-
定义
在随机变量的全集 U U U中,对于给定的变量 X ∈ U X\in U X∈U和变量集 M B ⊂ U ( X ∉ M B ) MB\subset U(X\notin MB) MB⊂U(X∈/MB),若有
X ⊥ { U − M B − { X } } ∣ M B (9.3.1) \color{red}X\perp \{U-MB-\{X\}\}|MB\tag{9.3.1} X⊥{U−MB−{X}}∣MB(9.3.1)
则称能满足上述条件的 最 小 变 量 集 M B \color{blue}最小变量集MB 最小变量集MB为 X X X的马尔可夫毯(Markov Blanket)。解释:
- 形象一点:把一个随机变量全集 U U U分成互斥的三部分,变量 X X X以及集合 A A A和 B B B,三个子集没有交集,并集即为全集 U U U;如果说给定集合 A A A时,变量 X X X与集合 B B B没有任何关系,则称集合 A A A为变量 X X X的马尔可夫毯。在式(9.3.1)中,集合 M B MB MB即为我说的集合 A A A, { U − M B − { X } } \{U-MB-\{X\}\} {U−MB−{X}}即为我说的集合 B B B,符号“ ⊥ \perp ⊥”表示“独立”,符号“ ∣ | ∣”表示在给定xx条件下,因此式(9.3.1)可读为“在给定集合 M B MB MB时,变量 X X X与 { U − M B − { X } } \{U-MB-\{X\}\} {U−MB−{X}}独立”。
- 具体举例理解:全集U是整个社会,X是你个人,MB就是你生活圈子里的人。按照哲学的说法,万事万物都是有联系的;但是,你并不会与社会里的所有人有什么关系,而是通过你的生活圈子和他们有间接的关系,即当给定你的生活圈子以后,你和社会其余的人是没啥关系的(独立的)。
-
概率推导
首先定义 x − i x_{-i} x−i为 { x 1 , x 2 , ⋯ , x i − 1 , x i + 1 , ⋯ , x N } \{x_1,x_2,\cdots,x_{i-1},x_{i+1},\cdots,x_N\} {x1,x2,⋯,xi−1,xi+1,⋯,xN},这个序列中唯独不包括 x i x_i xi。那么,假设除了 x i x_i xi节点,其他节点都是可观测的,那么计算概率:
p ( x i ∣ x − i ) = p ( x i , x − i ) p ( x − i ) = p ( x ) ∫ x i p ( x ) d x i = ∏ j = 1 N p ( x j ∣ x p a ( j ) ) ∫ x i ∏ j = 1 N p ( x j ∣ x p a ( j ) ) d x i . (9.3.2) p(x_i|x_{-i}) = \frac{p(x_i, x_{-i})}{p(x_{-i})} = \frac{p(x)}{\int_{x_i}p(x)dx_i} = \frac{\prod_{j=1}^N p(x_j|x_{pa(j)})}{\int_{x_i}\prod_{j=1}^N p(x_j|x_{pa(j)})dx_i}.\tag{9.3.2} p(xi∣x−i)=p(x−i)p(xi,x−i)=∫xip(x)dxip(x)=∫xi∏j=1Np(xj∣xpa(j))dxi∏j=1Np(xj∣xpa(j)).(9.3.2)分析一下上述等式,可以将其分成两部分,将和 x i x_i xi相关的部分记为 Δ ˉ \bar{\Delta} Δˉ,和 x i x_i xi不相关的部分记为 Δ \Delta Δ。公式(9.3.2)可以改写为:
p ( x i ∣ x − i ) = Δ ⋅ Δ ˉ ∫ x i Δ ⋅ Δ ˉ d x i = Δ ⋅ Δ ˉ Δ ⋅ ∫ x i Δ ˉ d x i = = Δ ˉ ∫ x i Δ ˉ d x i . (9.3.3) p(x_i|x_{-i})= \frac{\Delta\cdot \bar{\Delta}}{\int_{x_i}\Delta\cdot \bar{\Delta}dx_i} = \frac{\Delta\cdot \bar{\Delta}}{\Delta\cdot \int_{x_i} \bar{\Delta}dx_i} = = \frac{ \bar{\Delta}}{ \int_{x_i} \bar{\Delta}dx_i}.\tag{9.3.3} p(xi∣x−i)=∫xiΔ⋅ΔˉdxiΔ⋅Δˉ=Δ⋅∫xiΔˉdxiΔ⋅Δˉ==∫xiΔˉdxiΔˉ.(9.3.3)
就将 p ( x i ∣ x − i ) p(x_i|x_{-i}) p(xi∣x−i)表示为一个函数 f ( Δ ˉ ) f(\bar{\Delta}) f(Δˉ)。 x i 和 其 他 所 有 点 的 关 系 化 简 为 只 和 x i 相 关 的 点 的 关 系 \color{red}x_i和其他所有点的关系化简为只和x_i相关的点的关系 xi和其他所有点的关系化简为只和xi相关的点的关系。将这个关系大致抽象出来,通过图来进行分析,找一找哪些节点是和 x i x_i xi相关的,直观性也是概率图模型的一大优点。假设 x i x_i xi是可以被观测到的
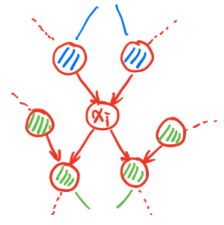
P ( x i ∣ x − 1 ) P(x_i|x_{-1}) P(xi∣x−1)首先包括一部分为 p ( x i ∣ x p a ( i ) ) p(x_i|x_{pa(i)}) p(xi∣xpa(i)),第二部分为 p ( x c h i l d ( i ) ∣ x i , x p a ( c h i l d ( x i ) ) ) p(x_{child(i)}|x_i,x_{pa(child(x_i))}) p(xchild(i)∣xi,xpa(child(xi)))。如图画阴影部分所示。为什么第二部分可以这样写呢?
首先 x i x_i xi作为两个父亲节点,得到两个孩子节点,毫无疑问对吧,那么我们可以写成 p ( x c h i l d ( i ) ∣ x i ) p(x_{child(i)}|x_i) p(xchild(i)∣xi)。但是和 p ( x c h i l d ( i ) ) p(x_{child(i)}) p(xchild(i))相关的变量除了 x i x_i xi肯定还有其他的,也就是 x p a ( c h i l d ( x i ) ) x_{pa(child(x_i))} xpa(child(xi)),所以我们就可以得到 p ( x c h i l d ( i ) ∣ x i , x p a ( c h i l d ( x i ) ) ) p(x_{child(i)}|x_i,x_{pa(child(x_i))}) p(xchild(i)∣xi,xpa(child(xi)))。 -
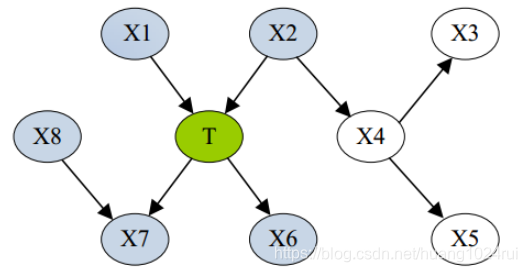
举例
在可信的贝叶斯网络中、一个结点的马尔可夫毯即为该结点的父节点、子节点以及子节点的父节点。在如图, M B ( T ) = { X 1 , X 2 , X 6 , X 7 , X 8 } MB(T)=\{X1 ,X2 ,X6 ,X7,X8\} MB(T)={X1,X2,X6,X7,X8}。
9.4 贝叶斯网络-Representation-具体模型例子
由于概率图是一个非常大的领域,不能一一详细的讲解每一个例子,所以从大的方面介绍一下贝叶斯网络的表示、推断和学习等模型通用的东西。本节介绍贝叶斯网络都有哪些类别及模型,进行一个简单的总结。
-
单一
单一最典型的代表就是Naive Bayesian,这是一种classification的模型。对于 p ( x ∣ y = 1 ) p(x|y=1) p(x∣y=1)的问题来说,假设各维度之间相互独立,于是就有:
p ( x ∣ y = 1 ) = ∏ i = 1 N p ( x i ∣ y = 1 ) . (9.4.1) p(x|y=1) = \prod_{i=1}^N p(x_i|y=1).\tag{9.4.1} p(x∣y=1)=i=1∏Np(xi∣y=1).(9.4.1)
概率图模型表示如下所示:
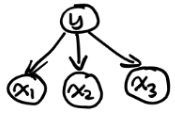
很显然是一个Tail to Tail的模型,我们很简单可以得出 x 1 ⊥ x 2 ⊥ ⋯ ⊥ x N x_1 \bot x_2 \bot \cdots \bot x_N x1⊥x2⊥⋯⊥xN。 -
混合
最常见的是Gaussian Mixture Model (GMM),这是一种聚类模型,将每个类别拟合一个分布,计算数据点和分布之间的关系来确定,数据点所属的类别。假设 Z Z Z是一个隐变量,并且 Z Z Z是离散的变量,那么 x ∣ z ∼ N ( μ , Σ ) x|z \sim \mathcal{N}(\mu,\Sigma) x∣z∼N(μ,Σ)。我们用模型可以表示为:

-
时间
- 时间上我们大致可以分成两种。第一种是Markov chain,这是随机过程中的一种;第二种事Gaussian Processing,实际上就是无限维的高斯分布。
- 实际上时间和混合可以一起看,我们称之为动态系统模型。并且,我们就可以衍生出三种常见的模型,这里讲的比较的模糊,在后面的章节我们会进行详细的分析。第一种是隐马尔可夫模型(HMM),这是一种离散的模型;第二种是线性动态系统(LDS),这是一种线性的连续的模型,包括典型的Kalman Filter。第三种是Particle Filter,一种非高斯的,非线性的模型。
-
连续
连续就是Guassian Bayesian Network,前面有提到过。 -
总结

- 总的来说,用两句话总结这些模型:
从 单 一 到 混 合 ; 从 有 限 到 无 限 。 \color{red}从单一到混合;\\ 从有限到无限。 从单一到混合;从有限到无限。 - 从有限到无限又可以分为两个角度:
- 空间(随机变量的取值从离散到连续)
- 时间(加入时间维度,从某一时刻延长到无限时间)
- 总的来说,用两句话总结这些模型:
9.5 马尔可夫随机场-Representation-条件独立性
-
上一小节,我们了解有向图Bayesian Network,学习了条件独立性、D-Seperation和因子分解( p ( x ) = ∏ i = 1 N p ( x i ∣ x p a ( i ) ) p(x) = \prod_{i=1}^N p(x_i|x_{pa(i)}) p(x)=∏i=1Np(xi∣xpa(i)))。虽然,有向图中可以方便直观的表达条件独立性,但是它也有局限性。即对于Head to Head的结构来说,当中间节点被观察到的时候,两端的节点反而是相关的,这违反了条件独立性的特点。
本节开始讲解Markov network(无向图的代表),其中也包含条件独立性和因子分解。
-
Markov中的条件独立,大致可以被我们分成三种情况,Global Markov,Local Markov和Pair Markov。三者之间满足: G l o b a l M a r k o v ⇔ L o c a l M a r k o v ⇔ P a i r M a r k o v . (9.5.1) \color{red}Global\;Markov\Leftrightarrow Local\;Markov\Leftrightarrow Pair\;Markov .\tag{9.5.1} GlobalMarkov⇔LocalMarkov⇔PairMarkov.(9.5.1)
- 全局马尔可夫性(Global Markov)
- 定义:在无向图中给定三个集合 A , B , C A,B,C A,B,C,在无向图中如果满足给定 X C X_C XC的条件下, X A X_A XA和 X B X_B XB相互独立,即 X A ⊥ X B ∣ X C \color{blue}X_{A}\perp X_{B}|X_{C} XA⊥XB∣XC,则满足全局马尔可夫性。
- 解释:在图中的判定方法为从
A
A
A中节点到
B
B
B中节点的任何路径上都至少有一个位于
C
C
C中的节点:

- 局部马尔可夫性(Local Markov)
- 定义:针对某个结点
a
a
a,当给定它的邻居结点时,它独立于其余结点。即:
a ⊥ { 全 集 − a − a 的 邻 居 } ∣ 邻 居 . (9.5.2) \color{red}a\bot \{全集-a-a的邻居\}|邻居.\tag{9.5.2} a⊥{全集−a−a的邻居}∣邻居.(9.5.2)
也可以写成: x ⊥ ( X − N e i g h b o r ( x ) − x ) ∣ N e i g h b o r ( x ) . (9.5.3) \color{red}x\perp (X-Neighbor(x)-x)|Neighbor(x).\tag{9.5.3} x⊥(X−Neighbor(x)−x)∣Neighbor(x).(9.5.3) - 举例:在下图对于节点
a
a
a,
x
⊥
{
e
,
f
}
∣
{
b
,
c
,
d
}
x\perp \left \{e,f\right \}|\left \{b,c,d\right \}
x⊥{e,f}∣{b,c,d}

- 定义:针对某个结点
a
a
a,当给定它的邻居结点时,它独立于其余结点。即:
- 成对马尔可夫性(Pair Markov)
成对马尔可夫性是指给定所有其他变量,两个非邻接变量条件独立,即:
x i ⊥ x j ∣ x − i − j 其 中 i ≠ j , x i , x j 不 相 邻 . (9.5.4) \color{red}x_{i}\perp x_{j}|x_{-i-j}\;其中i\neq j,x_{i},x_{j}不相邻.\tag{9.5.4} xi⊥xj∣x−i−j其中i=j,xi,xj不相邻.(9.5.4)
- 全局马尔可夫性(Global Markov)
9.6 马尔可夫随机场-Representation-因子分解
有向图中按照拓扑排序根据结点与其父结点的关系进行分解,但是在无向图中失去了方向性,从主观上来看,若 x i ⊥ x j x_{i}\perp x_{j} xi⊥xj那么, x i , x j x_{i},x_{j} xi,xj必然不在同一个因子里,从图上来看应该不是关联的。
-
团
- 团:一个关于结点的集合,集合中的结点之间相互都是连通的。(类似数据结构中的完全图)
- 最大团:在一个团中不能再添加任何结点,若添加后则不为团,称此团为最大团(数据结构中的极大连通子图)。
将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解。
-
因子分解
给定概率无向图模型, C i , i = 1 , 2 , ⋯ , k C_i,i=1,2,\cdots ,k Ci,i=1,2,⋯,k为无向图模型上的最大团,则 x x x的联合概率分布 P ( x ) P(x) P(x)可以写为:
p ( x ) = 1 Z ∏ i = 1 k ϕ ( x C i ) . (9.5.5) \color{red}p(x) = \frac{1}{Z}\prod_{i=1}^k \phi (x_{C_i}).\tag{9.5.5} p(x)=Z1i=1∏kϕ(xCi).(9.5.5)
其中, C i C_{i} Ci为最大团, x C i x_{C_{i}} xCi为最大团随机变量集合, ϕ ( x C i ) \phi (x_{C_{i}}) ϕ(xCi)为势函数(必须为正), Z Z Z是归一化因子。因为没有归一化因子的话,这不能被称为一个概率分布,因为概率分布要保证和等于 1 1 1。那么, Z Z Z可以写成:
z = ∑ x ∏ i = 1 k ϕ ( x C i ) = ∑ x 1 ∑ x 2 ⋯ ∑ x N ∏ i = 1 k ϕ ( x C i ) . (9.5.6) \color{red}z = \sum_x \prod_{i=1}^k\phi(x_{C_i}) = \sum_{x_1}\sum _{x_{2}}\cdots\sum_{x_N} \prod_{i=1}^k\phi(x_{C_i}).\tag{9.5.6} z=x∑i=1∏kϕ(xCi)=x1∑x2∑⋯xN∑i=1∏kϕ(xCi).(9.5.6)
其中 x x x有 N N N个点。 接 下 来 需 要 证 明 这 种 因 子 分 解 与 条 件 独 立 性 等 价 \color{blue}接下来需要证明这种因子分解与条件独立性等价 接下来需要证明这种因子分解与条件独立性等价。即:
G l o b a l M a r k o v ⇔ L o c a l M a r k o v ⇔ P a i r M a r k o v ⇔ H a m m e s l e y − C l i f f o r d 因 子 分 解 . (9.5.7) \color{red}Global\;Markov\Leftrightarrow Local\;Markov\Leftrightarrow Pair\;Markov\underset{Hammesley-Clifford}{ \Leftrightarrow} 因子分解.\tag{9.5.7} GlobalMarkov⇔LocalMarkov⇔PairMarkovHammesley−Clifford⇔因子分解.(9.5.7)
这个定理的证明非常的困难,我们这里就不做过多的阐述(有需求的小伙伴可以查下Hammesley-Clifford定理的证明)。 -
势函数
在我们之前的定义中,
p ( x ) = 1 Z ∏ i = 1 k ϕ ( x C i ) p(x) = \frac{1}{Z}\prod_{i=1}^k \phi(x_{C_i}) p(x)=Z1i=1∏kϕ(xCi)
其中 c i c_i ci为最大团; x c i x_{c_i} xci为最大团的随机变量集合; ϕ ( x c i ) \phi(x_{c_i}) ϕ(xci)为势函数,必须为正。势函数的概念是来自于统计物理学和热力学的过程。- 势函数必定为正,我们可以将势函数表达为
ϕ
(
x
c
i
)
=
exp
{
−
E
(
x
c
i
)
}
\phi(x_{c_i}) = \exp\{ -E(x_{c_i}) \}
ϕ(xci)=exp{−E(xci)}。其中,
E
(
x
c
i
)
E(x_{c_i})
E(xci)称为Energy function。实际上用这种形式表达的
p
(
x
)
p(x)
p(x),为Gibbs Distribution,或者又被称之为Boltzman Distribution。可以写成:
p ( x ) = 1 Z ∏ i = 1 K ϕ ( x c i ) = 1 Z ∏ i = 1 K exp { − E ( x c i ) } = 1 Z exp { − ∑ i = 1 k E ( x c i ) } . (9.5.8) p(x) = \frac{1}{Z}\prod_{i=1}^K\phi(x_{c_i}) = \frac{1}{Z}\prod_{i=1}^K \exp\{ -E(x_{c_i}) \} = \frac{1}{Z}\exp\{ - \sum_{i=1}^k E(x_{c_i}) \}.\tag{9.5.8} p(x)=Z1i=1∏Kϕ(xci)=Z1i=1∏Kexp{−E(xci)}=Z1exp{−i=1∑kE(xci)}.(9.5.8) - 指数族分布与势函数
我们将指数族分布和势函数联系起来:
p ( x ) = h ( x ) exp { η T ϕ ( x ) − A ( η ) } = h ( x ) 1 Z ( η ) exp { η T ϕ ( x ) } . (9.5.9) p(x) = h(x)\exp\{ \eta^T\phi(x) - A(\eta) \} = h(x)\frac{1}{Z(\eta)}\exp\{ \eta^T\phi(x)\}.\tag{9.5.9} p(x)=h(x)exp{ηTϕ(x)−A(η)}=h(x)Z(η)1exp{ηTϕ(x)}.(9.5.9)
发现势函数(Gibbs Distribution)是一个指数族分布。Gibbs是来自统计物理学,形式上和指数族分布时一样的。而指数族分布实际上是由最大熵分布得到的,那么我们可以理解Gibbs分布也是有最大熵原理得到的。而马尔可夫随机场(Markov Random Field)实际上等价于Gibbs分布。即:
最 大 熵 原 理 ⇒ 指 数 族 分 布 ( G i b b s 分 布 ) . (9.5.10) \color{red}{最大熵原理\Rightarrow 指数族分布(Gibbs分布)}.\tag{9.5.10} 最大熵原理⇒指数族分布(Gibbs分布).(9.5.10)
M a r k o v R a n d o m F i e l d ⇔ G i b b s D i s t r i b u t i o n . (9.5.11) \color{red}{Markov\ Random\ Field \Leftrightarrow Gibbs \ Distribution}.\tag{9.5.11} Markov Random Field⇔Gibbs Distribution.(9.5.11)
- 势函数必定为正,我们可以将势函数表达为
ϕ
(
x
c
i
)
=
exp
{
−
E
(
x
c
i
)
}
\phi(x_{c_i}) = \exp\{ -E(x_{c_i}) \}
ϕ(xci)=exp{−E(xci)}。其中,
E
(
x
c
i
)
E(x_{c_i})
E(xci)称为Energy function。实际上用这种形式表达的
p
(
x
)
p(x)
p(x),为Gibbs Distribution,或者又被称之为Boltzman Distribution。可以写成:
总结
- 马尔科夫随机场
- Global Markov: X A ⊥ X C ∣ X B X_A \bot X_C | X_B XA⊥XC∣XB。如果 A , B , C , A,B,C, A,B,C,满足 S e p ( A , C ∣ B ) Sep(A,C|B) Sep(A,C∣B),Sep代表D-Separation,那么 X A ⊥ X C ∣ X B X_A \bot X_C | X_B XA⊥XC∣XB。
- Local Markov Network: x i ⊥ x − i − n b ( i ) ∣ x n b ( i ) x_i\bot x_{-i-nb(i)}|x_{nb(i)} xi⊥x−i−nb(i)∣xnb(i),其实nb(i):neighbor of node i。
- Pair Markov: x i ⊥ x j ∣ x − i − j x_i \bot x_j|x_{-i-j} xi⊥xj∣x−i−j。
- 因子分解:
p
(
x
)
=
1
Z
∏
i
=
1
k
ϕ
(
x
C
i
)
p(x) = \frac{1}{Z}\prod_{i=1}^k \phi(x_{C_i})
p(x)=Z1∏i=1kϕ(xCi)
四者之间的关系:
G l o b a l M a r k o v ⇔ L o c a l M a r k o v ⇔ P a i r M a r k o v ⇔ H a m m e s l e y − C l i f f o r d 因 子 分 解 \color{red}Global\;Markov\Leftrightarrow Local\;Markov\Leftrightarrow Pair\;Markov\underset{Hammesley-Clifford}{ \Leftrightarrow} 因子分解 GlobalMarkov⇔LocalMarkov⇔PairMarkovHammesley−Clifford⇔因子分解
- 势函数
- 势函数必定为正,可以表达为
ϕ
(
x
c
i
)
=
exp
{
−
E
(
x
c
i
)
}
\phi(x_{c_i}) = \exp\{ -E(x_{c_i}) \}
ϕ(xci)=exp{−E(xci)}。其中,
E
(
x
c
i
)
E(x_{c_i})
E(xci)称为Energy function。实际上用这种形式表达的
p
(
x
)
p(x)
p(x),为Gibbs Distribution,或者又被称之为Boltzman Distribution。
最 大 熵 原 理 ⇒ 指 数 族 分 布 ( G i b b s 分 布 ) M a r k o v R a n d o m F i e l d ⇔ G i b b s D i s t r i b u t i o n . \color{red}{最大熵原理\Rightarrow 指数族分布(Gibbs分布)}\\ \color{red}{Markov\ Random\ Field \Leftrightarrow Gibbs \ Distribution}. 最大熵原理⇒指数族分布(Gibbs分布)Markov Random Field⇔Gibbs Distribution.
- 势函数必定为正,可以表达为
ϕ
(
x
c
i
)
=
exp
{
−
E
(
x
c
i
)
}
\phi(x_{c_i}) = \exp\{ -E(x_{c_i}) \}
ϕ(xci)=exp{−E(xci)}。其中,
E
(
x
c
i
)
E(x_{c_i})
E(xci)称为Energy function。实际上用这种形式表达的
p
(
x
)
p(x)
p(x),为Gibbs Distribution,或者又被称之为Boltzman Distribution。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








