9. 概率图模型之推断
9.7 推断Inference-总体介绍
-
定义
推断(Inference)这个词,对于学过机器学习的同学来说,一定听说,这也是贝叶斯方法中一个非常重要的理论性研究。那么什么是推断呢?推断就是 求 概 率 \color{red}求概率 求概率。比如,对联合概率密度函数 p ( x ) = p ( x 1 , x 2 , ⋯ , x p ) p(x)=p(x_1,x_2,\cdots,x_p) p(x)=p(x1,x2,⋯,xp)。我们需要求的有哪些呢?- 边缘概率: p ( x i ) = ∑ x 1 ⋯ ∑ x i − 1 ⋯ ∑ x i + 1 ⋯ ∑ x p p ( x ) p(x_i) = \sum_{x_1}\cdots\sum_{x_{i-1}}\cdots\sum_{x_{i+1}}\cdots\sum_{x_p}p(x) p(xi)=∑x1⋯∑xi−1⋯∑xi+1⋯∑xpp(x)。
- 条件概率: p ( x A ∣ x B ) p(x_A|x_B) p(xA∣xB),令 x = x A ∪ x B x=x_A\cup x_B x=xA∪xB。
- MAP Inference(最大后验概率推断):也就是 z ^ = a r g m a x z p ( z ∣ x ) ∝ a r g m a x p ( x , z ) \hat{z} = argmax_z\ p(z|x) \varpropto argmax \ p(x,z) z^=argmaxz p(z∣x)∝argmax p(x,z)。 p ( z ∣ x ) = p ( x , z ) p ( x ) ∝ p ( x , z ) p(z|x) = \frac{p(x,z)}{p(x)} \varpropto p(x,z) p(z∣x)=p(x)p(x,z)∝p(x,z)是因为目标是求最优的参数 z z z,所以 p ( x ) p(x) p(x)可以不看。
-
Inference求解方法
- 精确推断:
- Variable Elimination(VE,变量消除法)(针对树结构);
- Belief Propagation(BP,信念传播,又称Sum-Product Algorithm)(针对树结构);
- Junction Tree Algorithm(针对图结构,是BP算法在普通图结构上的扩展)
- 近似推断:
- Loop Belief Propagation(针对有环图);
- Mente Carlo Inference(基于采样问题)(例如:Importance Sampling,MCMC);
- Variational Inference(变分推断)
- 精确推断:
-
举例:隐马尔可夫模型(Hidden Markov Model)
Hidden Markov Model (HMM)算法将在后面做详细的描述,在这一小节中,主要进行概述。HMM的模型可视化为上图所示,其中 O O O是隐变量,也就是我们的观测变量。
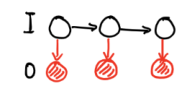
我们主要考虑三个问题,在三个问题为Inference的问题:- Evaluation,求边缘密度
P
(
O
)
=
∑
I
P
(
I
,
O
)
P(O) = \sum_I P(I,O)
P(O)=∑IP(I,O)。 计算量非常大,可采用两种算法:
- 前向:使用递推式从前往后走
- 后向:从最后一个时刻往前走
- Learning,也就是寻找 λ ^ \hat{\lambda} λ^。
- Decoding: I ^ = a r g m a x I P ( I ∣ O ) \hat{I} = argmax_I P(I|O) I^=argmaxIP(I∣O),属于MAP Inference,包括Vitebi Algorithm,这是一个动态规划算法。
隐马尔可夫模型实际上一种动态规划模型(Dynamic Bayesian Network)。
- Evaluation,求边缘密度
P
(
O
)
=
∑
I
P
(
I
,
O
)
P(O) = \sum_I P(I,O)
P(O)=∑IP(I,O)。 计算量非常大,可采用两种算法:
9.8 推断Inference-Variable Elimination
上一小节介绍了推断的背景和分类,我们知道大致推断的方法。推断的任务为:给定已知的 p ( x ) = ( x 1 , x 2 , ⋯ , x p ) p(x) = (x_1,x_2,\cdots,x_p) p(x)=(x1,x2,⋯,xp),求:
- 边缘概率: p ( x i ) = ∑ x 1 , ⋯ , x i − 1 , x i + 1 , ⋯ , x p p ( x 1 , x 2 , ⋯ , x p ) p(x_i) = \sum_{x_1,\cdots,x_{i-1},x_{i+1},\cdots,x_p}p(x_1,x_2,\cdots,x_p) p(xi)=∑x1,⋯,xi−1,xi+1,⋯,xpp(x1,x2,⋯,xp)。
- 条件概率: p ( x A ∣ x B ) p(x_A|x_B) p(xA∣xB),也就是在已知 x B x_B xB集合的情况下,如何求得 x A x_A xA集合的概率。
- 最大后验概率(MAP): x ^ A = a r g m a x x A p ( x A ∣ x B ) = a r g m a x p ( x A , x B ) \hat{x}_A=argmax_{x_A}p(x_A|x_B) = argmax\ p(x_A,x_B) x^A=argmaxxAp(xA∣xB)=argmax p(xA,xB)。
下面介绍最简单的一个精确推断,名为变量消除法(Variable Elimination)。虽然简单,也是推断法的核心概念之一。
- 问题描述
假如我们有一个马氏链:

对于上述图结构,假如我们希望求边缘概率 p ( d ) p(d) p(d),根据公式我们可以得到:
p ( d ) = ∑ a , b , c p ( a , b , c , d ) . (9.8.1) p(d) = \sum_{a,b,c}p(a,b,c,d).\tag{9.8.1} p(d)=a,b,c∑p(a,b,c,d).(9.8.1)
然后使用因子分解,我们可以得到:
p ( d ) = ∑ a , b , c p ( a ) p ( b ∣ a ) p ( c ∣ b ) p ( d ∣ c ) . (9.8.2) p(d) = \sum_{a,b,c}p(a)p(b|a)p(c|b)p(d|c).\tag{9.8.2} p(d)=a,b,c∑p(a)p(b∣a)p(c∣b)p(d∣c).(9.8.2)
假定, a , b , c , d a,b,c,d a,b,c,d都为均匀离散的二值random variable,所以 a , b , c , d ∈ { 0 , 1 } a,b,c,d\in \{0,1\} a,b,c,d∈{0,1}。所以将P(d)展开:
P ( d ) = ∑ a , b , c P ( a , b , c , d ) = ∑ a , b , c P ( a ) P ( b ∣ a ) P ( c ∣ b ) P ( d ∣ c ) = P ( a = 0 ) P ( b = 0 ∣ a = 0 ) P ( c = 0 ∣ b = 0 ) P ( d ∣ c = 0 ) + P ( a = 0 ) P ( b = 0 ∣ a = 0 ) P ( c = 1 ∣ b = 0 ) P ( d ∣ c = 1 ) + P ( a = 0 ) P ( b = 1 ∣ a = 0 ) P ( c = 0 ∣ b = 1 ) P ( d ∣ c = 0 ) + P ( a = 0 ) P ( b = 1 ∣ a = 0 ) P ( c = 1 ∣ b = 1 ) P ( d ∣ c = 1 ) + P ( a = 1 ) P ( b = 0 ∣ a = 1 ) P ( c = 0 ∣ b = 0 ) P ( d ∣ c = 0 ) + P ( a = 1 ) P ( b = 0 ∣ a = 1 ) P ( c = 1 ∣ b = 0 ) P ( d ∣ c = 1 ) + P ( a = 1 ) P ( b = 1 ∣ a = 1 ) P ( c = 0 ∣ b = 1 ) P ( d ∣ c = 0 ) + P ( a = 1 ) P ( b = 1 ∣ a = 1 ) P ( c = 1 ∣ b = 1 ) P ( d ∣ c = 1 ) = 8 ⋅ 因 子 积 . (9.8.3) P(d)=\sum _{a,b,c}P(a,b,c,d) =\sum _{a,b,c}P(a)P(b|a)P(c|b)P(d|c)\\ =P(a=0)P(b=0|a=0)P(c=0|b=0)P(d|c=0)\\ +P(a=0)P(b=0|a=0)P(c=1|b=0)P(d|c=1)\\ +P(a=0)P(b=1|a=0)P(c=0|b=1)P(d|c=0)\\ +P(a=0)P(b=1|a=0)P(c=1|b=1)P(d|c=1)\\ +P(a=1)P(b=0|a=1)P(c=0|b=0)P(d|c=0)\\ +P(a=1)P(b=0|a=1)P(c=1|b=0)P(d|c=1)\\ +P(a=1)P(b=1|a=1)P(c=0|b=1)P(d|c=0)\\ +P(a=1)P(b=1|a=1)P(c=1|b=1)P(d|c=1) =8\cdot 因子积.\tag{9.8.3} P(d)=a,b,c∑P(a,b,c,d)=a,b,c∑P(a)P(b∣a)P(c∣b)P(d∣c)=P(a=0)P(b=0∣a=0)P(c=0∣b=0)P(d∣c=0)+P(a=0)P(b=0∣a=0)P(c=1∣b=0)P(d∣c=1)+P(a=0)P(b=1∣a=0)P(c=0∣b=1)P(d∣c=0)+P(a=0)P(b=1∣a=0)P(c=1∣b=1)P(d∣c=1)+P(a=1)P(b=0∣a=1)P(c=0∣b=0)P(d∣c=0)+P(a=1)P(b=0∣a=1)P(c=1∣b=0)P(d∣c=1)+P(a=1)P(b=1∣a=1)P(c=0∣b=1)P(d∣c=0)+P(a=1)P(b=1∣a=1)P(c=1∣b=1)P(d∣c=1)=8⋅因子积.(9.8.3)
可以看出计算非常复杂,若变量取值有 k k k个,变量个数为 p p p个,则计算复杂度为 k p k^p kp。 - 计算
如果(9.8.3)直接计算,每一项再加起来就会需要相当大的计算量。变量消除法就是根据某些节点只与图中自己的邻接节点有关这一特性来简化计算,相当于应用了 乘 法 分 配 律 \color{red}乘法分配律 乘法分配律( a b + a c = a ( b + c ) ab+ac=a(b+c) ab+ac=a(b+c))来避免计算每一项在加起来。变量消除法在上式中的计算过程为:
P ( d ) = ( 将 与 a 有 关 的 放 到 一 起 ) = P ( c = 0 ∣ b = 0 ) P ( d ∣ c = 0 ) ⋅ P ( a = 0 ) P ( b = 0 ∣ a = 0 ) + P ( c = 1 ∣ b = 0 ) P ( d ∣ c = 1 ) ⋅ P ( a = 0 ) P ( b = 0 ∣ a = 0 ) + P ( c = 0 ∣ b = 1 ) P ( d ∣ c = 0 ) ⋅ P ( a = 0 ) P ( b = 1 ∣ a = 0 ) + P ( c = 1 ∣ b = 1 ) P ( d ∣ c = 1 ) ⋅ P ( a = 0 ) P ( b = 1 ∣ a = 0 ) + P ( c = 0 ∣ b = 0 ) P ( d ∣ c = 0 ) ⋅ P ( a = 1 ) P ( b = 0 ∣ a = 1 ) + P ( c = 1 ∣ b = 0 ) P ( d ∣ c = 1 ) ⋅ P ( a = 1 ) P ( b = 0 ∣ a = 1 ) + P ( c = 0 ∣ b = 1 ) P ( d ∣ c = 0 ) ⋅ P ( a = 1 ) P ( b = 1 ∣ a = 1 ) + P ( c = 1 ∣ b = 1 ) P ( d ∣ c = 1 ) ⋅ P ( a = 1 ) P ( b = 1 ∣ a = 1 ) ( 应 用 乘 法 分 配 律 ) = P ( c = 0 ∣ b = 0 ) P ( d ∣ c = 0 ) ⋅ ϕ a ( b = 0 ) + P ( c = 1 ∣ b = 0 ) P ( d ∣ c = 1 ) ⋅ ϕ a ( b = 0 ) + P ( c = 0 ∣ b = 1 ) P ( d ∣ c = 0 ) ⋅ ϕ a ( b = 1 ) + P ( c = 1 ∣ b = 1 ) P ( d ∣ c = 1 ) ⋅ ϕ a ( b = 1 ) ( 将 与 b 有 关 的 放 到 一 起 ) = P ( d ∣ c = 0 ) ⋅ P ( c = 0 ∣ b = 0 ) ϕ a ( b = 0 ) + P ( d ∣ c = 1 ) ⋅ P ( c = 1 ∣ b = 0 ) ϕ a ( b = 0 ) + P ( d ∣ c = 0 ) ⋅ P ( c = 0 ∣ b = 1 ) ϕ a ( b = 1 ) + P ( d ∣ c = 1 ) ⋅ P ( c = 1 ∣ b = 1 ) ϕ a ( b = 1 ) ( 应 用 乘 法 分 配 律 ) = P ( d ∣ c = 0 ) ⋅ ϕ b ( c = 0 ) + P ( d ∣ c = 1 ) ⋅ ϕ b ( c = 1 ) = ϕ c ( d ) . (9.8.4) P(d)= (将与a有关的放到一起)\\ ={\color{Red}{P(c=0|b=0)P(d|c=0)\cdot P(a=0)P(b=0|a=0)}}\\ +{\color{Green}{P(c=1|b=0)P(d|c=1)\cdot P(a=0)P(b=0|a=0)}}\\ +{\color{Blue}{P(c=0|b=1)P(d|c=0)\cdot P(a=0)P(b=1|a=0)}}\\ +{\color{Black}{P(c=1|b=1)P(d|c=1)\cdot P(a=0)P(b=1|a=0)}}\\ +{\color{Red}{P(c=0|b=0)P(d|c=0)\cdot P(a=1)P(b=0|a=1)}}\\ +{\color{Green}{P(c=1|b=0)P(d|c=1)\cdot P(a=1)P(b=0|a=1)}}\\ +{\color{Blue}{P(c=0|b=1)P(d|c=0)\cdot P(a=1)P(b=1|a=1)}}\\ +{\color{Black}{P(c=1|b=1)P(d|c=1)\cdot P(a=1)P(b=1|a=1)}}\\ (应用乘法分配律)\\ ={\color{Red}{P(c=0|b=0)P(d|c=0)\cdot \phi _{a}(b=0)}} +{\color{Green}{P(c=1|b=0)P(d|c=1)\cdot \phi _{a}(b=0)}}\\ +{\color{Blue}{P(c=0|b=1)P(d|c=0)\cdot \phi _{a}(b=1)}} +{\color{Black}{P(c=1|b=1)P(d|c=1)\cdot \phi _{a}(b=1)}}\\ (将与b有关的放到一起)\\ ={\color{Red}{P(d|c=0)\cdot P(c=0|b=0)\phi _{a}(b=0)}}+{\color{Green}{P(d|c=1)\cdot P(c=1|b=0)\phi _{a}(b=0)}}\\ +{\color{Red}{P(d|c=0)\cdot P(c=0|b=1)\phi _{a}(b=1)}} +{\color{Green}{P(d|c=1)\cdot P(c=1|b=1)\phi _{a}(b=1)}}\\ (应用乘法分配律)\\ ={\color{Red}{P(d|c=0)\cdot \phi _{b}(c=0)}} +{\color{Green}{P(d|c=1)\cdot \phi _{b}(c=1)}} =\phi _{c}(d).\tag{9.8.4} P(d)=(将与a有关的放到一起)=P(c=0∣b=0)P(d∣c=0)⋅P(a=0)P(b=0∣a=0)+P(c=1∣b=0)P(d∣c=1)⋅P(a=0)P(b=0∣a=0)+P(c=0∣b=1)P(d∣c=0)⋅P(a=0)P(b=1∣a=0)+P(c=1∣b=1)P(d∣c=1)⋅P(a=0)P(b=1∣a=0)+P(c=0∣b=0)P(d∣c=0)⋅P(a=1)P(b=0∣a=1)+P(c=1∣b=0)P(d∣c=1)⋅P(a=1)P(b=0∣a=1)+P(c=0∣b=1)P(d∣c=0)⋅P(a=1)P(b=1∣a=1)+P(c=1∣b=1)P(d∣c=1)⋅P(a=1)P(b=1∣a=1)(应用乘法分配律)=P(c=0∣b=0)P(d∣c=0)⋅ϕa(b=0)+P(c=1∣b=0)P(d∣c=1)⋅ϕa(b=0)+P(c=0∣b=1)P(d∣c=0)⋅ϕa(b=1)+P(c=1∣b=1)P(d∣c=1)⋅ϕa(b=1)(将与b有关的放到一起)=P(d∣c=0)⋅P(c=0∣b=0)ϕa(b=0)+P(d∣c=1)⋅P(c=1∣b=0)ϕa(b=0)+P(d∣c=0)⋅P(c=0∣b=1)ϕa(b=1)+P(d∣c=1)⋅P(c=1∣b=1)ϕa(b=1)(应用乘法分配律)=P(d∣c=0)⋅ϕb(c=0)+P(d∣c=1)⋅ϕb(c=1)=ϕc(d).(9.8.4)
我们就可以把这么一长串的公式进行逐步化简了,这就是变量消元的思想。 - 推广
- 上述都以链为例,将其推广到图:
- 先使用因子分解
- 然后逐步针对每一个结点,对与之相关的概率先计算
主要思想还是 分 配 率 \color{red}分配率 分配率!
- 同样在无向图中,我们也可以使用到马尔可夫网络中。使用最大团分解:
p ( a , b , c , d ) = 1 z ∏ i = 1 k ϕ c i ( x c i ) . (9.8.5) p(a,b,c,d) = \frac{1}{z}\prod_{i=1}^k \phi_{c_i}(x_{c_i}).\tag{9.8.5} p(a,b,c,d)=z1i=1∏kϕci(xci).(9.8.5)
由于是最大团,不能再添加其他结点,因此团与团的联系较小,同时每一个结点几乎不可能同时存在于所有团,因此同样可以使用Variable Elimination方法进行计算。
- 上述都以链为例,将其推广到图:
- 局限性
- 计算重复性
上述例子只计算了结点 d d d,若需要计算其他结点,又要重新计算,每次计算的中间结果没有存储,导致重复计算。 - 计算次序
变量消除的次序会决定时间复杂度,最优次序的寻找已被证明是一个NP-Hard问题,因此也可以使用一些启发式思想进行次序选择。
- 计算重复性
9.9 推断Inference-Belief Propagation(1)
上一小节介绍了变量消除(Variable Elimination)(核心是: 乘 法 对 加 法 的 分 配 律 \color{red}乘法对加法的分配律 乘法对加法的分配律),Variable Elimination的思想是Probability Graph中的核心思想之一。但Variable Elimination中存在重复计算和最优计算次序不好确定的问题。所以,这一节介绍Belief Propagation来解决重复计算的问题。
9.9.1 Belief Propagation思想(Variable Elimination的计算重复问题)
对于下图马氏链模型:

- 已知联合概率:
P ( a , b , c , d , e ) = P ( a ) P ( b ∣ a ) P ( c ∣ b ) P ( d ∣ c ) P ( e ∣ d ) . (9.9.1) P(a,b,c,d,e)=P(a)P(b|a)P(c|b)P(d|c)P(e|d).\tag{9.9.1} P(a,b,c,d,e)=P(a)P(b∣a)P(c∣b)P(d∣c)P(e∣d).(9.9.1) - 计算
P
(
e
)
\color{blue}P(e)
P(e)的边缘概率时,使用变量消除法的步骤如下:
P ( e ) = ∑ a , b , c , d P ( a , b , c , d , e ) = ∑ d P ( e ∣ d ) ∑ c P ( d ∣ c ) ∑ b P ( c ∣ b ) ∑ a P ( b ∣ a ) P ( a ) = ∑ d P ( e ∣ d ) ∑ c P ( d ∣ c ) ∑ b P ( c ∣ b ) m a → b ( b ) = ∑ d P ( e ∣ d ) ∑ c P ( d ∣ c ) m b → c ( c ) = ∑ d P ( e ∣ d ) m c → d ( d ) = m d → e ( e ) . (9.9.2) \begin{array}{l} P(e)=\sum_{a,b,c,d} P(a,b,c,d,e)\\ =\sum_dP(e|d)\sum_cP(d|c)\sum_bP(c|b)\sum_aP(b|a)P(a)\\ =\sum_dP(e|d)\sum_cP(d|c)\sum_bP(c|b) \color{red}{m_{a\to b}(b)}\\ =\sum_dP(e|d)\sum_cP(d|c) \color{red}{m_{b\to c}(c)}\\ =\sum_dP(e|d) \color{red}{m_{c\to d}(d)}\\ = \color{red}{m_{d\to e}(e)}\\ \end{array}.\tag{9.9.2} P(e)=∑a,b,c,dP(a,b,c,d,e)=∑dP(e∣d)∑cP(d∣c)∑bP(c∣b)∑aP(b∣a)P(a)=∑dP(e∣d)∑cP(d∣c)∑bP(c∣b)ma→b(b)=∑dP(e∣d)∑cP(d∣c)mb→c(c)=∑dP(e∣d)mc→d(d)=md→e(e).(9.9.2)
相当于沿着这个链这个马氏链一直往前走,也就是 前 向 算 法 ( F o r w a r d A l g o r i t h m ) \color{blue}前向算法(Forward Algorithm) 前向算法(ForwardAlgorithm)。我们用公式表达即为:
a ⟶ m a ⟶ b ( b ) b ⟶ m b ⟶ c ( c ) c ⟶ m c ⟶ d ( d ) d ⟶ m d ⟶ e ( e ) e . (9.9.3) \color{red}a \stackrel{m_{a\longrightarrow b}(b)}{\longrightarrow} b \stackrel{m_{b\longrightarrow c}(c)}{\longrightarrow} c \stackrel{m_{c\longrightarrow d}(d)}{\longrightarrow} d \stackrel{m_{d\longrightarrow e}(e)}{\longrightarrow} e.\tag{9.9.3} a⟶ma⟶b(b)b⟶mb⟶c(c)c⟶mc⟶d(d)d⟶md⟶e(e)e.(9.9.3) - 计算
P
(
c
)
\color{blue}P(c)
P(c)的边缘概率时,使用变量消除法的步骤如下:
P ( c ) = ∑ a , b , d , e P ( a , b , c , d , e ) = ∑ a , b , d , e P ( a ) P ( b ∣ a ) P ( c ∣ b ) P ( d ∣ c ) P ( e ∣ d ) = ( ∑ b P ( c ∣ b ) ∑ a P ( b ∣ a ) P ( a ) ) ⋅ ( ∑ c P ( d ∣ c ) ∑ d P ( e ∣ d ) ) . (9.9.4) P(c)=\sum_{a,b,d,e}P(a,b,c,d,e)\\ =\sum_{a,b,d,e}P(a)P(b|a)P(c|b)P(d|c)P(e|d)\\ =(\sum_{b}P(c|b)\sum_{a}P(b|a)P(a))\cdot (\sum_{c}P(d|c)\sum_{d}P(e|d)).\tag{9.9.4} P(c)=a,b,d,e∑P(a,b,c,d,e)=a,b,d,e∑P(a)P(b∣a)P(c∣b)P(d∣c)P(e∣d)=(b∑P(c∣b)a∑P(b∣a)P(a))⋅(c∑P(d∣c)d∑P(e∣d)).(9.9.4)
这里,我们就不仅用 前 向 算 法 \color{blue}前向算法 前向算法来解决了,需要用到 F o r w a r d − B a c k w a r d 算 法 \color{blue}Forward-Backward算法 Forward−Backward算法来解决了。传递过程为: a ⟶ b ⟶ c ⟵ d ⟵ e a\longrightarrow b \longrightarrow c \longleftarrow d \longleftarrow e a⟶b⟶c⟵d⟵e。
a ⟶ m a ⟶ b ( b ) b ⟶ m b ⟶ c ( c ) c ⟵ m c ⟵ d ( c ) d ⟵ m d ⟵ e ( d ) e . (9.9.5) \color{red}a \stackrel{m_{a\longrightarrow b}(b)}{\longrightarrow} b \stackrel{m_{b\longrightarrow c}(c)}{\longrightarrow} c \stackrel{m_{c\longleftarrow d}(c)}{\longleftarrow} d \stackrel{m_{d\longleftarrow e}(d)}{\longleftarrow} e.\tag{9.9.5} a⟶ma⟶b(b)b⟶mb⟶c(c)c⟵mc⟵d(c)d⟵md⟵e(d)e.(9.9.5) - 对比上面的计算 p ( e ) p(e) p(e)的过程,可以发现, ∑ b p ( c ∣ b ) ∑ a p ( b ∣ a ) p ( a ) \sum_b p(c|b)\sum_a p(b|a)p(a) ∑bp(c∣b)∑ap(b∣a)p(a)部分( m b ⟶ c ( c ) m_{b\longrightarrow c}(c) mb⟶c(c))是一模一样的。所以Variable Elimination里面有大量的重复计算。Belief的想法就是将 m i ⟶ j ( j ) m_{i\longrightarrow j}(j) mi⟶j(j) 全部事先计算好,就像一个个积木一样,然后再用这个积木来搭建运算。 那么也就是:事先将方向全部定义好,正向和反向的全部都求了再说。为了进一步探究Belief Background,我们需要讨论更加Generalize的情况: 从 C h a i n ⟶ T r e e \color{blue}从Chain\longrightarrow Tree 从Chain⟶Tree, 有 向 ⟶ 无 项 \color{blue}有向\longrightarrow无项 有向⟶无项的情况。
9.9.2 Belief Propagation的扩展
Generalize后,分析了一个树形的无向图结构。图的网络结构如下所示:
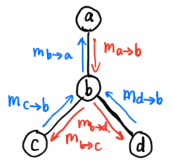
该图的联合概率的因子分解可以写为:
P
(
a
,
b
,
c
,
d
)
=
1
Z
ψ
a
(
a
)
ψ
b
(
b
)
ψ
c
(
c
)
ψ
d
(
d
)
⋅
ψ
a
b
(
a
,
b
)
ψ
b
c
(
b
,
c
)
ψ
b
d
(
b
,
d
)
.
(9.9.6)
P(a,b,c,d)=\frac{1}{Z}\psi _{a}(a)\psi _{b}(b)\psi _{c}(c)\psi _{d}(d)\cdot \psi _{ab}(a,b) \psi _{bc}(b,c) \psi _{bd}(b,d).\tag{9.9.6}
P(a,b,c,d)=Z1ψa(a)ψb(b)ψc(c)ψd(d)⋅ψab(a,b)ψbc(b,c)ψbd(b,d).(9.9.6)
- 求解边缘概率
P
(
a
)
P(a)
P(a)
应用到变量消除法,大体步骤是先消去 c c c和 d d d,然后再消去 b b b,该过程如下所示:
p ( a ) = ψ a ∑ b ψ b ⋅ ψ a b ( ∑ c ψ c ⋅ ψ b c ⏟ m c → b ( b ) ) ( ∑ d ψ d ⋅ ψ b d ⏟ m d → b ( b ) ) ⏟ m b → a ( a ) . (9.9.7) p(a)=\psi _{a}\underset{m_{b\rightarrow a}(a)}{\underbrace{\sum _{b}\psi _{b}\cdot \psi _{ab}(\underset{m_{c\rightarrow b}(b)}{\underbrace{\sum _{c}\psi _{c}\cdot \psi _{bc}}})(\underset{m_{d\rightarrow b}(b)}{\underbrace{\sum _{d}\psi _{d}\cdot \psi _{bd}}})}}.\tag{9.9.7} p(a)=ψamb→a(a) b∑ψb⋅ψab(mc→b(b) c∑ψc⋅ψbc)(md→b(b) d∑ψd⋅ψbd).(9.9.7)- 求解的过程主要就是求以下两项(这里写得规范一些,比如
a
a
a写作
x
a
x_a
xa):
{ m b → a ( x a ) = ∑ x b ψ a b ⋅ ψ b ⋅ m c → b ( x b ) ⋅ m d → b ( x b ) p ( x a ) = ψ a ⋅ m b → a ( x a ) (9.9.8) \left\{\begin{matrix} m_{b\rightarrow a}(x_{a})=\sum _{x_{b}}\psi _{ab}\cdot \psi _{b}\cdot m_{c\rightarrow b}(x_{b})\cdot m_{d\rightarrow b}(x_{b})\\ p(x_{a})=\psi _{a}\cdot m_{b\rightarrow a}(x_{a}) \end{matrix}\right.\tag{9.9.8} {mb→a(xa)=∑xbψab⋅ψb⋅mc→b(xb)⋅md→b(xb)p(xa)=ψa⋅mb→a(xa)(9.9.8) - 将求解
x
a
x_{a}
xa边缘概率的过程抽象出来得到求解
x
i
x_{i}
xi边缘概率的过程:
{ m j → i ( x i ) = ∑ x j ψ i j ⋅ ψ j ⋅ ∏ k ∈ N e i g h b o r ( j ) − i m k → j ( x j ) p ( x i ) = ψ i ⋅ ∏ k ∈ N e i g h b o r ( j ) m k → i ( x i ) (9.9.9) \color{blue}\left\{\begin{matrix} m_{j\rightarrow i}(x_{i})=\sum _{x_{j}}\psi _{ij}\cdot \psi _{j}\cdot \prod _{k\in Neighbor(j)-i}m_{k\rightarrow j}(x_{j})\\ p(x_{i})=\psi _{i}\cdot \prod _{k\in Neighbor(j)} m_{k\rightarrow i}(x_{i}) \end{matrix}\right.\tag{9.9.9} {mj→i(xi)=∑xjψij⋅ψj⋅∏k∈Neighbor(j)−imk→j(xj)p(xi)=ψi⋅∏k∈Neighbor(j)mk→i(xi)(9.9.9) - 续观察求解
x
i
x_{i}
xi边缘概率的公式,并对一些部分做一下定义:
{ m j → i ( x i ) = ∑ x j ψ i j ⋅ ψ j ⏟ s e l f ⋅ ∏ k ∈ N e i g h b o r ( j ) − i m k → j ( x j ) ⏟ c h i l d r e n ⏟ b e l i e f ( x j ) p ( x i ) = ψ i ⋅ ∏ k ∈ N e i g h b o r ( j ) m k → i ( x i ) (9.9.10) \color{red}\left\{\begin{matrix} m_{j\rightarrow i}(x_{i})=\sum _{x_{j}}\psi _{ij}\cdot\underset{belief(x_{j})}{ \underbrace{\underset{self}{\underbrace{\psi _{j}}}\cdot \underset{children}{\underbrace{\prod _{k\in Neighbor(j)-i}m_{k\rightarrow j}(x_{j})}}}}\\ p(x_{i})=\psi _{i}\cdot \prod _{k\in Neighbor(j)} m_{k\rightarrow i}(x_{i}) \end{matrix}\right.\tag{9.9.10} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧mj→i(xi)=∑xjψij⋅belief(xj) self ψj⋅children k∈Neighbor(j)−i∏mk→j(xj)p(xi)=ψi⋅∏k∈Neighbor(j)mk→i(xi)(9.9.10)
- 求解的过程主要就是求以下两项(这里写得规范一些,比如
a
a
a写作
x
a
x_a
xa):
- 总结
求解 m j → i ( x i ) \color{blue}m_{j\rightarrow i}(x_{i}) mj→i(xi)需要两步:
{ b e l i e f ( x j ) = s e l f ⋅ c h i l d r e n m j → i ( x i ) = ∑ x j ψ i j ⋅ b e l i e f ( x j ) (9.9.11) \color{red}\left\{\begin{matrix} belief(x_{j})=self\cdot children\\ m_{j\rightarrow i}(x_{i})=\sum _{x_{j}}\psi _{ij}\cdot belief(x_{j}) \end{matrix}\right.\tag{9.9.11} {belief(xj)=self⋅childrenmj→i(xi)=∑xjψij⋅belief(xj)(9.9.11)
根据避免重复计算的思路,可得出结论: 不 要 直 接 去 求 边 缘 概 率 密 度 ( p ( a ) , p ( b ) , p ( c ) , p ( d ) ) \color{red}不要直接去求边缘概率密度(p(a),p(b),p(c),p(d)) 不要直接去求边缘概率密度(p(a),p(b),p(c),p(d)),可以 先 建 立 一 个 C a c h e , 算 出 m i ⟶ j , 然 后 直 接 进 行 搭 建 和 拼 接 。 \color{red}先建立一个Cache,算出m_{i\longrightarrow j},然后直接进行搭建和拼接。 先建立一个Cache,算出mi⟶j,然后直接进行搭建和拼接。 从这里,引出了Belief Propagation(信念传播)。即:
B P = V E + c a c h BP=VE+cach BP=VE+cach
cach是计算所有的 m j → i m_{j \to i } mj→i。
9.10 推断Inference-Belief Propagation(2)
上节知道了BP(Belief Propagation)算法,BP算法实质是图的遍历或者树的遍历。BP算法的一般过程如下:
-
BP(sequential)

- Get Root: 首先假设一个节点为根节点。
- Collect Message: 对于每一个在根节点的邻接点中的节点
x
i
x_i
xi,Collect Message (
x
i
x_i
xi)。对应图中蓝色的线条。
for xi in NB(Root): Collect Message(xi) - Distribute Message: 对于每一个在根节点的邻接点中的节点
x
i
x_i
xi,Distribute Message (
x
i
x_i
xi)。对应图中红色的线条。
for xi in NB(Root): Distribute Message(xi)
通过以上三步,可得所有的 m i → j ∀ i , j ∈ V ( V 是 所 有 点 的 集 合 ) m_{i\to j}\ \ \forall i,j \in V(V是所有点的集合) mi→j ∀i,j∈V(V是所有点的集合),从而求得 P ( x k ) , k ∈ V P(x_k),k \in V P(xk),k∈V。
-
BP(Parellel Implementation)
这种方法采用并行分布式的方法- 随机找一个点 x x x;
- 求信息量 (刚开始只有 ψ x \psi _x ψx);
- 向他的邻居结点发生通知,邻居结点收到通知后进行同样的操作;
- 然后将消息传递回去。
最终会收敛,求得所有的 m i → j m_{i \to j} mi→j,此方法的优点是可以 并 行 计 算 \color{red}并行计算 并行计算。
9.11 推断Inference-Max Product
-
概率图模型
概率图模型是对于一个图,Graph = { X , E } \{ X,E \} {X,E},其中 X X X代表的是普通变量, E E E代表的是Evidence,也就是观测变量。概率图模型需要解决的是:
1. 边 缘 变 量 \color{blue}边缘变量 边缘变量
也就是已知: E = { e 1 , e 2 , ⋯ , e k } E=\{ e_1,e_2,\cdots,e_k \} E={e1,e2,⋯,ek},如何求 p ( E ) p(E) p(E)的问题,其中 E E E为一个变量或者为一个子集。实际上就是一个likelihood的问题。
2. 条 件 概 率 \color{blue}条件概率 条件概率
也就是一个求后验概率的问题,目标概率为 X = ( Y , Z ) X=(Y,Z) X=(Y,Z)。而 p ( Y ∣ E ) = ∑ z p ( X ∣ E ) p(Y|E) = \underset{z}{\sum} p(X|E) p(Y∣E)=z∑p(X∣E)。
3. 最 大 后 验 估 计 ( M A P ) \color{blue}最大后验估计(MAP) 最大后验估计(MAP)
也被我们称为Decoding的问题。也就是我们希望找到一个隐序列,使得: x ^ = a r g m a x x P ( X ∣ E ) \hat{x} = \underset{x}{argmax} P(X|E) x^=xargmaxP(X∣E), y ^ = a r g m a x y P ( Y ∣ E ) \hat{y} = \underset{y}{argmax} P(Y|E) y^=yargmaxP(Y∣E)。
Max-Product算法其实:- 从算法上是 B e l i e f P r o p a g a t i o n 算 法 的 改 进 \color{red}Belief Propagation算法的改进 BeliefPropagation算法的改进;
- 从模型上是 H M M 中 V i t e r b i 算 法 的 推 广 \color{red}HMM中Viterbi算法的推广 HMM中Viterbi算法的推广。
-
Belief Propagation算法的改进
对于下图,BP算法和Max Product Algorithm计算 P ( x a ) P(x_a) P(xa):
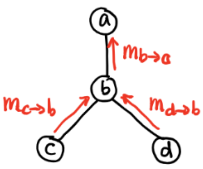
- 运用Belief Propagation
{ m b → a ( x a ) = ∑ x b ψ a b ⋅ ψ b ⋅ m c → b ( x b ) ⋅ m d → b ( x b ) p ( x a ) = ψ a ⋅ m b → a ( x a ) (9.11.1) \left\{\begin{matrix} \underset{b\rightarrow a}{m}(x_{a})=\underset{x_{b}}{\sum}\psi _{ab}\cdot \psi _{b}\cdot \underset{c\rightarrow b}{m}(x_{b})\cdot \underset{d\rightarrow b}{m}(x_{b})\\ p(x_{a})=\psi _{a}\cdot \underset{b\rightarrow a}{m}(x_{a}) \end{matrix}\right.\tag{9.11.1} ⎩⎨⎧b→am(xa)=xb∑ψab⋅ψb⋅c→bm(xb)⋅d→bm(xb)p(xa)=ψa⋅b→am(xa)(9.11.1)
即:
p ( a ) = ψ a ∑ b ψ b ⋅ ψ a b ( ∑ c ψ c ⋅ ψ b c ⏟ m c → b ( b ) ) ( ∑ d ψ d ⋅ ψ b d ⏟ m d → b ( b ) ) ⏟ m b → a ( a ) . (9.11.2) \color{red}p(a)=\psi _{a}\underset{m_{b\rightarrow a}(a)}{\underbrace{\sum _{b}\psi _{b}\cdot \psi _{ab}(\underset{m_{c\rightarrow b}(b)}{\underbrace{\sum _{c}\psi _{c}\cdot \psi _{bc}}})(\underset{m_{d\rightarrow b}(b)}{\underbrace{\sum _{d}\psi _{d}\cdot \psi _{bd}}})}}.\tag{9.11.2} p(a)=ψamb→a(a) b∑ψb⋅ψab(mc→b(b) c∑ψc⋅ψbc)(md→b(b) d∑ψd⋅ψbd).(9.11.2) - 运用Max-Product Algorithm
求解过程如下:
① m c → b = m a x x c ψ c ⋅ ψ b c . (9.11.3) ①\; m_{c\rightarrow b} =\underset{x_{c}}{max}\; \psi _{c}\cdot \psi _{bc}.\tag{9.11.3} ①mc→b=xcmaxψc⋅ψbc.(9.11.3)
把 ψ c ⋅ ψ b c \psi _{c}\cdot \psi _{bc} ψc⋅ψbc看作是一个关于 x c x_{c} xc的函数,也就是找到这个函数的最大值。
② m d → b = m a x x d ψ d ⋅ ψ b d . (9.11.4) ②\; m_{d\rightarrow b} =\underset{x_{d}}{max}\; \psi _{d}\cdot \psi _{bd}.\tag{9.11.4} ②md→b=xdmaxψd⋅ψbd.(9.11.4)
把 ψ d ⋅ ψ b d \psi _{d}\cdot \psi _{bd} ψd⋅ψbd看作是一个关于 x d x_{d} xd的函数,也就是找到这个函数的最大值。同理:
③ m b → a = m a x x b ψ b ⋅ ψ a b ⋅ m c → b ⋅ m d → b . (9.11.5) ③\; m_{b\rightarrow a} =\underset{x_{b}}{max}\; \psi _{b}\cdot \psi _{ab}\cdot m_{c\rightarrow b}\cdot m_{d\rightarrow b}.\tag{9.11.5} ③mb→a=xbmaxψb⋅ψab⋅mc→b⋅md→b.(9.11.5)
最后求解 x a x_{a} xa,得:
④ m a x P ( x a , x b , x c , x d ) = m a x x a ψ a ⋅ m b → a . (9.11.6) ④\; max\; P(x_{a},x_{b},x_{c},x_{d})=\underset{x_{a}}{max}\; \psi _{a}\cdot m_{b\rightarrow a}.\tag{9.11.6} ④maxP(xa,xb,xc,xd)=xamaxψa⋅mb→a.(9.11.6)
因此,Max-Product Algorithm可以写成:
( x a ∗ , x b ∗ , x c ∗ , x d ∗ ) = a r g m a x x a , x b , x c , x d P ( x a , x b , x c , x d ∣ E ) . (9.11.7) \color{red}(x_{a}^{*},x_{b}^{*},x_{c}^{*},x_{d}^{*})=\underset{x_{a},x_{b},x_{c},x_{d}}{argmax}\; P(x_{a},x_{b},x_{c},x_{d}|E).\tag{9.11.7} (xa∗,xb∗,xc∗,xd∗)=xa,xb,xc,xdargmaxP(xa,xb,xc,xd∣E).(9.11.7) - 总结
通过公式(9.11.2)和公式(9.11.7)可得:- Belief Propagation算法可以看作是
S
u
m
P
r
o
d
u
c
t
A
l
g
o
r
i
t
h
m
\color{red}Sum\;Product\;Algorithm
SumProductAlgorithm,即:
m j → i ( x i ) = ∑ j ψ i , j ψ j ∏ k ∈ N B ( j ) m k → j ( x j ) . (9.11.8) \color{blue}m_{j\to i}(x_i)=\sum_j \psi_{i,j} \psi_j \prod_{k\in NB(j)}m_{k \to j}(x_j).\tag{9.11.8} mj→i(xi)=j∑ψi,jψjk∈NB(j)∏mk→j(xj).(9.11.8) - Max-Product Algorithm则可以认为是
S
u
m
M
a
x
P
r
o
d
u
c
t
A
l
g
o
r
i
t
h
m
\color{red}Sum\;Max\;Product\;Algorithm
SumMaxProductAlgorithm,即:
m j → i ( x i ) = max j ψ i , j ψ j ∏ k ∈ N B ( j ) m k → j ( x j ) . (9.11.9) \color{blue}m_{j\to i}(x_i)=\underset{j}{\max}\ \psi_{i,j} \psi_j \prod_{k\in NB(j)}m_{k \to j}(x_j).\tag{9.11.9} mj→i(xi)=jmax ψi,jψjk∈NB(j)∏mk→j(xj).(9.11.9)
- Belief Propagation算法可以看作是
S
u
m
P
r
o
d
u
c
t
A
l
g
o
r
i
t
h
m
\color{red}Sum\;Product\;Algorithm
SumProductAlgorithm,即:
- 运用Belief Propagation
-
Viterbi算法的推广
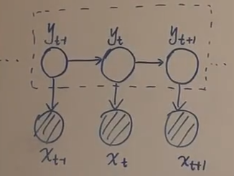
如图在HMM中解决Decoding问题需要求解 Y Y Y的隐状态序列(图中虚线框),即求解: Y ^ = a r g m a x Y P ( Y ∣ X ) \hat Y=arg\underset {Y}{max}P(Y|X) Y^=argYmaxP(Y∣X)。此问题使用Vitebi算法求解,是一种 动 态 规 划 \color{red}动态规划 动态规划的思想。Viterbi的思路:使用 δ t \delta_t δt代表从时刻 1 1 1到时刻 t t t中, 当 Y = y ^ 1 , y ^ 2 , ⋯ , y ^ t Y=\hat y_1,\hat y_2,\cdots,\hat y_t Y=y^1,y^2,⋯,y^t时对应的最大概率值,然后找到 δ t \delta_t δt与 δ t + 1 \delta_{t+1} δt+1的关系,最终将可以求得最优值 δ T \delta_T δT,之后进行反向tracking,找到最优的状态序列。
Max-Product Algorithm 思想与Vitebi算法类似,不过是对Vitebi算法的推广,从在链上使用推广到树上使用。所以Max-Product算法其实:
- 算法上:是 B e l i e f P r o p a g a t i o n 算 法 的 改 进 \color{red}Belief\;Propagation算法的改进 BeliefPropagation算法的改进;
- 模型上:是 H M M 中 V i t e r b i 算 法 的 推 广 \color{red}HMM中Viterbi算法的推广 HMM中Viterbi算法的推广。
9.12 道德图(Moral Graph)
这一小节补充一个概念:道德图(Moral Graph)。引入道德图的原因: 将 有 向 图 转 为 无 向 图 \color{red}将有向图转为无向图 将有向图转为无向图。转换后将不需要区分有向图和无向图,只需要研究无向图即可。
- 在概率图中,我们可以分为贝叶斯网络(有向图) 和 马尔可夫网络(无向图)。
- 无向图可以表示为:
p ( x ) = 1 z ∏ i = 1 k ϕ c i ( x c i ) . (9.12.1) p(x) = \frac{1}{z}\prod_{i=1}^k \phi_{c_i}(x_{c_i}).\tag{9.12.1} p(x)=z1i=1∏kϕci(xci).(9.12.1) - 有向图可以表示为:
p ( x ) = ∏ i = 1 p p ( x i ∣ x p a ( i ) ) . (9.12.2) p(x) = \prod_{i=1}^pp(x_i|x_{pa(i)}).\tag{9.12.2} p(x)=i=1∏pp(xi∣xpa(i)).(9.12.2)
其中, ϕ c i \phi_{c_i} ϕci代表的是最大团的意思。通过道德图,我们可以有效的将有向图转换为无向图。
- 无向图可以表示为:
- 三种基本有向图转换成无向图
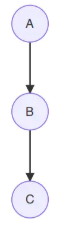
- 链式(head to tail)
 ⟶
\longrightarrow
⟶
⟶
\longrightarrow
⟶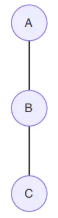
用公式表达为: P ( A , B , C ) = P ( A ) P ( B ∣ A ) ⏟ ϕ ( A , B ) P ( C ∣ B ) ⏟ ϕ ( B , C ) . (9.12.3) P(A,B,C)=\underset{\phi (A,B)}{\underbrace{P(A)P(B|A)}}\underset{\phi (B,C)}{\underbrace{P(C|B)}}.\tag{9.12.3} P(A,B,C)=ϕ(A,B) P(A)P(B∣A)ϕ(B,C) P(C∣B).(9.12.3)
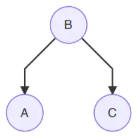
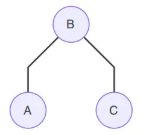
这说明A,B和B,C是团,因此可以直接去掉箭头。 - V形(tail to tail)
 ⟶
\longrightarrow
⟶
⟶
\longrightarrow
⟶
用公式表达为:
P ( A , B , C ) = P ( B ) P ( A ∣ B ) ⏟ ϕ ( A , B ) P ( C ∣ B ) ⏟ ϕ ( B , C ) . (9.12.4) P(A,B,C)=\underset{\phi (A,B)}{\underbrace{P(B)P(A|B)}}\underset{\phi (B,C)}{\underbrace{P(C|B)}}.\tag{9.12.4} P(A,B,C)=ϕ(A,B) P(B)P(A∣B)ϕ(B,C) P(C∣B).(9.12.4)
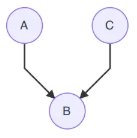
这说明A,B和B,C是团,因此可以直接去掉箭头。 - 倒V形(head to head)
 ⟶
\longrightarrow
⟶
⟶
\longrightarrow
⟶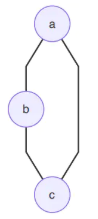
用公式表达为:
P ( A , B , C ) = P ( B ∣ A ) P ( B ) P ( B ∣ C ) ⏟ ϕ ( A , B , C ) . (9.12.5) P(A,B,C)=\underset{\phi (A,B,C)}{\underbrace{P(B|A)P(B)P(B|C)}}.\tag{9.12.5} P(A,B,C)=ϕ(A,B,C) P(B∣A)P(B)P(B∣C).(9.12.5)
说明A,B,C是一个团,需要在A,C之间加一条线。
- 链式(head to tail)
- 总结
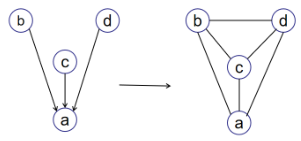
- 观察这三种情况可以将有向图到无向图的转换方法的步骤概括为:
① 将 每 个 节 点 的 ⽗ 节 点 两 两 相 连 \color{red}①将每个节点的⽗节点两两相连 ①将每个节点的⽗节点两两相连;
② 将 有 向 边 替 换 为 ⽆ 向 边 \color{red}②将有向边替换为⽆向边 ②将有向边替换为⽆向边。 - 举例:
- 意义
在判断条件独立性的时候,有时图形非常复杂的时候。我们在有向图中很难看出来,而在无向图中却可以很简单的得到我们想要的结果。也就是 S e p ( A , B ∣ C ) ⟺ D − S e p ( A , B ∣ C ) Sep(A,B|C) \Longleftrightarrow D-Sep(A,B|C) Sep(A,B∣C)⟺D−Sep(A,B∣C)。
- 观察这三种情况可以将有向图到无向图的转换方法的步骤概括为:
9.13 Factor Graph
上一节讲的道德图可以将有向图转换为无向图,但是可能会引入环(head-to-head类型),可能变成图,但是之前讲的BP(Belief Propagation)算法只能在树上操作,只能对树进行分解。
-
定义
因此需要引入因子图(Factor Graph),此方法有两大出发点:- 消 去 环 \color{red}消去环 消去环
- 简 便 \color{red}简便 简便
因子图的公式为:
p ( x ) = ∏ S p ( x S ) . (9.13.1) p(x) = \prod_{S}p(x_S).\tag{9.13.1} p(x)=S∏p(xS).(9.13.1)
其中, S S S是图的节点子集, x S x_S xS为对应的 X X X的子集,也就是 X X X的随机变量的子集。 -
举例
下图进行分解:
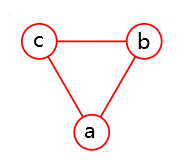
- 方法1
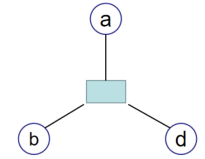
可以描述为: p ( x ) = f = f ( a , b , c ) p(x)=f = f(a,b,c) p(x)=f=f(a,b,c)。 - 方法2
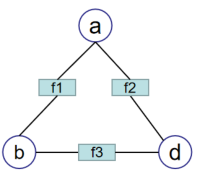
也可以描述为:
p ( x ) = f 1 ( a , b ) f 2 ( a , c ) f 3 ( b , c ) . (9.13.2) p(x) = f_1(a,b)f_2(a,c)f_3(b,c).\tag{9.13.2} p(x)=f1(a,b)f2(a,c)f3(b,c).(9.13.2) - 方法3
不仅是可以在两个节点之间插入关系,同时也可以对于单个节点引入函数。
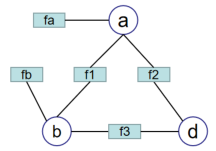
表达式为:
p ( x ) = f 1 ( a , b ) f 2 ( a , c ) f 3 ( b , c ) f a ( a ) f b ( b ) . (9.13.3) p(x) = f_1(a,b)f_2(a,c)f_3(b,c)f_a(a)f_b(b).\tag{9.13.3} p(x)=f1(a,b)f2(a,c)f3(b,c)fa(a)fb(b).(9.13.3)
上图可以看成是对因式分解的进一步分解,可以成功的消除环结构。如下图所示:
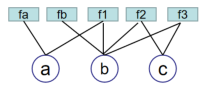
通过上面的三种方法,可以看到因子图存在的意义,它可以有效的 消 除 环 结 构 \color{red}消除环结构 消除环结构,通过一个重构的方式,重建出树的结构。这样可以有效的帮助我们使用Belief Propagation中的变量消除法等方法。
- 方法1























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








