python——numpy——random模块及常见分布模拟

最新推荐文章于 2025-02-03 14:05:14 发布

xia ge tou lia

最新推荐文章于 2025-02-03 14:05:14 发布

阅读量8k

点赞数 18

分类专栏： pyhton 概率论统计学

本文链接：https://blog.csdn.net/huangguohui_123/article/details/105160163

版权

pyhton 同时被 3 个专栏收录

44 篇文章

订阅专栏

统计学

30 篇文章

订阅专栏

概率论

6 篇文章

订阅专栏

一、随机数

1、numpy.random.rand()

生成均匀分布的随机小数。

rand函数根据给定维度生成[0,1)之间的数据，包含0，不包含1
括号参数为生成随机数的维度

一维数据

import numpy as np
import matplotlib.pyplot as plt
sample=np.random.rand(1000) #生成1000个(0,1]之间的小数。
plt.hist(sample)

输出：

二维数组

import numpy as np
np.random.rand(4,3)

输出：

array([[0.98518453, 0.44079493, 0.16225772],
       [0.77958445, 0.7090924 , 0.9106563 ],
       [0.92259129, 0.83041676, 0.61209929],
       [0.85128995, 0.82769906, 0.54040777]])

2、numpy.random.uniform()

生成[a, b)的均匀分布

sample=np.random.uniform(0, 5, size=2000)  #生成2000个0~5均匀分布的小数。
plt.hist(sample)

输出：

3、numpy.random.random()

与numpy.random.rand() 基本一致，生成均匀分布的随机小数。

4、numpy.random.randint()

返回均匀分布的随机整数。

范围区间为[low,high），包含low，不包含high
参数：low为最小值，high为最大值，size为数组维度，dtype为数据类型，默认的数据类型是np.int
high没有填写时，默认生成随机数的范围是[0，low)

一维数组

import numpy as np
import matplotlib.pyplot as plt
sample=np.random.randint(0,10,size=2000) #生成2000个(0,10]之间的整数。
plt.hist(sample)

输出：

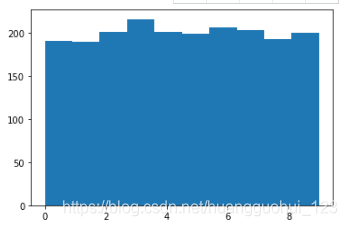
由上图可知，是均匀分布的。

二维数组

np.random.randint(-5,10) # 返回1个[-5,10)的随机整数
np.random.randint(-5,5,size=(2,2)) #size表示数组的维度

输出：

8
array([[ 0,  3],
       [-4,  1]])

5、numpy.random.randn()

返回一个或一组样本，具有标准正态分布
标准正态分布是以0为均值、以1为标准差的正态分布，记为N（0，1）。

import numpy as np
import matplotlib.pyplot as plt
sample=np.random.randn(2000) #生成2000个符合正态分布的浮点数。
plt.hist(sample)

输出：

同样，也可以生成二维数组：

np.random.randn(4,3)

输出：

array([[ 1.51323436e+00, -1.22829798e+00,  5.33658337e-01],
       [ 1.40142822e-03,  2.25463274e+00, -8.96981887e-02],
       [-5.13055770e-01,  2.38286579e+00,  7.84135515e-01],
       [ 4.20508288e-01, -8.41135019e-02, -2.07081489e+00]])

二、随机分布

二项分布和泊松分布属于离散型随机变量的分布，指数分布和正态分布属于连续型随机变量的分布。

1、np.random.binomial() 二项分布（贝努力分布）

二项分布的概率函数 P(X) 可用公式

$P(X)=C_{n}^{X}\pi^{X}(1-\pi )^{n-X}$

其中， $C_{n}^{X}=\frac{n!}{X!(n-X)!}$

最常见的二项分布就是投硬币问题了，投n次硬币，正面朝上次数就满足该分布。下面我们使用计算机模拟的方法，产生1000个符合 $(n,\pi )$ 的二项分布随机数，相当于进行1000次实验，每次实验投掷了n枚硬币，正面朝上的硬币数就是所产生的随机数。同时使用直方图函数绘制出二项分布的PMF图。

def plot_binomial(n,p):
    sample = np.random.binomial(n,p,size=1000)  # 产生1000个符合二项分布的随机数
    bins = np.arange(n+2) 
    plt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
    plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
    plt.hist(sample, bins=bins, align='left', density=True, rwidth=0.1)  # bins也就是总共有几条条状图,density表示条形图的总面积为1.
    #设置标题和坐标
    plt.title('概率质量分布：n={}, π={}'.format(n,p))  
    plt.xlabel('正面次数')
    plt.ylabel('概率')
    plt.show()
plot_binomial(10,0.5)

输出：

投10枚硬币，如果正面或反面朝上的概率相同，即π=0.5，那么出现正面次数的分布符合上图所示的二项分布。该分布左右对称，最有可能的情况是正面出现5次。

当π=0.2或者0.8时：

fig=plt.figure(figsize=(8,4))
ax=fig.add_subplot(1,2,1) 
plot_binomial(10,0.2)
ax=fig.add_subplot(1,2,2) 
plot_binomial(10,0.8)

输出：

2、np.random.poisson() 泊松分布

泊松分布分布一般记作 $P(\lambda )$ ，其概率函数为:

$P(X)=e^{-\lambda }\frac{\lambda ^{X}}{X!}$

式中， $\lambda=n\pi$ 为Poisson分布的总体均数( $\pi$ 表示概率)；为观察单位内某稀有事件的发生次数；为自然对数的底，为常数，约等于2.71828，自然对数的底数e是由一个重要极限给出的：当x趋于无限时， $\lim_{n \to +\propto }(1+\frac{1}{n})^n=e$ 。

比如你在等公交车，假设这些公交车的到来是独立且随机的，前后车之间没有关系，那么在1小时中到来的公交车数量就符合泊松分布。同样使用统计模拟的方法绘制该泊松分布，这里假设每小时平均来6辆车（即上述公式中 $\lambda$ =6）。

lamb = 6
sample = np.random.poisson(lamb, size=1000)  # 生成1000个符合泊松分布的随机数
bins = np.arange(20)
plt.hist(sample, bins=bins, align='left', rwidth=0.1, density=True) # bins也就是总共有几条条状图,density表示条形图的总面积为1.
plt.title('概率质量分布 (λ=6)')
plt.xlabel('一小时内公交车到达数量')
plt.ylabel('概率')
plt.show()

输出：

3、np.random.exponential() 指数分布

设随机变量X的分布密度函数为

$f(x)=\left\{\begin{matrix} \lambda e^{-\lambda x},x>0\\ 0,x\leq 0 \end{matrix}\right.$

指数分布通常用作各种“寿命”的分布。例如，无线电元件的寿命，动物的寿命等，另外电话问题的通话时间、随机服务系统中的服务时间等都可以认为服从指数分布，因此，它在排队论和可靠性理论等领域中有广泛的应用。

比如上面等公交车的例子，两辆车到来的时间间隔，就符合指数分布。假设平均间隔为10分钟（即1/ $\lambda$ =10)，那么从上次发车开始，你等车的时间就满足下图所示的指数分布。

t = 10
sample = np.random.exponential(t, size=10000)  # 产生10000个满足指数分布的随机数
plt.rcParams['font.sans-serif']=['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.hist(sample, bins=80, alpha=0.7, density=True) # bins也就是总共有几条条状图,density表示条形图的总面积为1.
plt.margins(0.02) 

# 根据公式绘制指数分布的概率密度函数
lam = 1 / t
x = np.arange(0,80,0.1)
y = lam * np.exp(- lam * x)
plt.plot(x,y,color='orange', lw=3)#设置标题和坐标轴
plt.title('指数概率密度函数, 1/λ=10')
plt.xlabel('时间')
plt.ylabel('概率')
plt.show()

输出：

4、np.random.normal() 正态分布

正态分布的概率密度函数（即纵向的曲线高度）

$f(X)=\frac{1}{\sigma \sqrt{2\pi }}e^{-\frac{1}{2}(\frac{X-\mu }{\sigma })^{2}}$ ， $-\infty < X< +\infty$

$\sigma$ 规定了曲线的形状， $\mu$ 反应了其在横轴上的位置不同。

绘制了 $\mu$ （均值）为0， $\sigma$ （标准差）为1的正态分布的概率密度曲线。

#根据概率密度函数，计算y值
def normal_pdf(x,mu,sigma):
    normal_pdf = np.exp(-(((x - mu)/sigma)**2) / 2) / (sigma * np.sqrt(2*np.pi))    
    return normal_pdf

mu = 0    # 均值为0
sigma = 1 # 标准差为1
# 用统计模拟绘制正态分布的直方图
sample = np.random.normal(mu, sigma, size=2000)
plt. hist(sample, bins=100, alpha=0.7, density=True)# bins也就是总共有几条条状图,density表示条形图的总面积为1.
x = np.arange(-5, 5, 0.01)  
y = normal_pdf(x, mu, sigma)
plt.plot(x,y, color='r', lw=3) #lw代表线的粗度
plt.show()

输出：