统计推断——假设检验——线性回归——R的平方可以为负数

在《统计推断——假设检验——简单线性回归分析》，我们学到了一个回归模型评价指标：决定系数。

回顾一下决定系数的公式：，其中代表离差总平方和，代表残差平方和，代表回归平方和，各指标计算如下所示：

例如下图中，P表示某一个观察点。

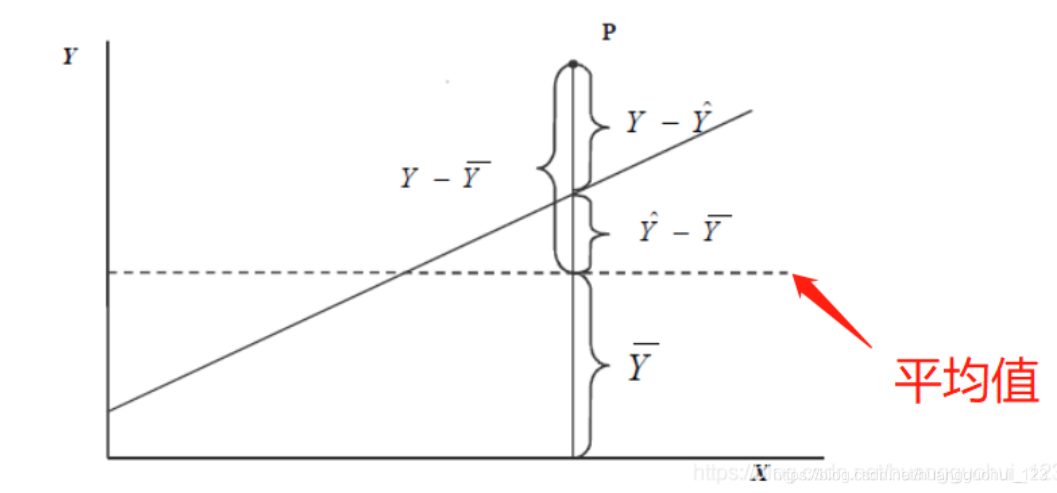
则根据：，根据上图进行分解：。

我们以下面数据为例，以生成点：

 生成的数据点及如下图所示.，在图中，蓝线上的数据是我们生成的数据，水平红线是该数据的平均值。这样根据公式我们就可以求出。

此数据的线性回归方程为，将代入可以求出相应的，然后根据公式，我们可以求得残差平方和。

最后根据公式：

算出来决定系数，那么如何定义它的效益呢？

• 为1.0最佳。这意味着你的回归模型没有错误。
• 为0表示你的回归并不比取平均值更好，即你没有使用其他变量中的任何信息。
• 为负表示你的回归模型的表现比平均值还差。

下面我们来考虑一个问题，可以为负吗？什么时候为负？

通过上面我们知道：任何大于零的都意味着回归分析比仅使用一条穿过平均值的水平线要好。在极少数情况下，你会得到负值，你可能应该重新考虑回归分析，尤其是在强制进行截距的情况下。

我们还是继续上面的数据进行讨论，我们随便找个线性回归方程为，如下图黑线代表，将代入可以求出相应的，然后根据公式，我们可以求得残差平方和。

最后根据公式：。

这个时候我们计算出来的就变成了负数，他代表的意义在于：该线性回归模型（黑线）对数据的拟合效果，还不如均值模型（红线）。在现实应用中，很少会出现这么离谱的情况，所以一般认为有用的模型的的取值范围在0-1之间。