Matlab实现——捕食者-被捕食者模型

欢迎前往个人博客 驽马点滴 和视频空间 哔哩哔哩-《挨踢日志》

问题重述：

捕食者－被捕食者模型非线性微分方程的一个例子是捕食者－被捕食者模型。设x(t)和y(t)分别表示兔子和狐狸在时刻t的数量，捕食者－被捕食者模型表明，x(t)和y(t)满足：

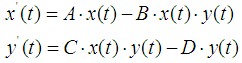
一个典型的计算机模拟可作用系数：

A=2,    B=0.02,    C=0.0002,    D=0.8

且满足：

x(0)=3000只兔子，y(0)=120只狐狸。

在区间[0,5]内：

(1)    用Euler法、Heun法和经典4阶Runge-kutta法取多种步长求解。

把x=x(t) 和y=y(t)画在同一张图上并给以解释。

(2) 为考察变量x和y之间的关系，将计算结果画在以x、y为坐标的图上，对所得结果加以解释。

 

原理介绍：

Euler Method

对于

dx=f(t,x,y)dt和dy=g(t,x,y)dt

将 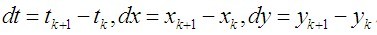代入上式得到：

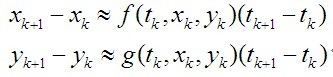
将区间分为M个子区间，宽度h=(b-a)/M,网格点为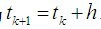

于是得到Euler Method:

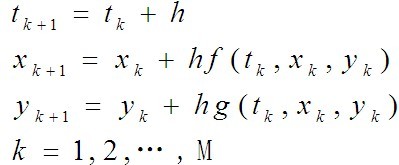
Heun Method

在区间[ , ]上对微分方程积分：

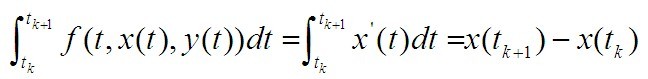
再利用trapezoidal rule可以得到：

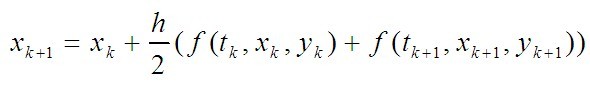
但右边含有，利用Euler Method 得到Heun Method：

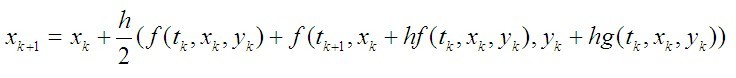
在每一步中，用Euler Method 作为预报，trapezoidal rule 进行校正，得到最终值。Heun Method的一般步骤如下：

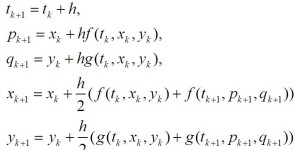
Runge-Kutta Method of Order 4

基于Heum Method 的推导过程，我们得到

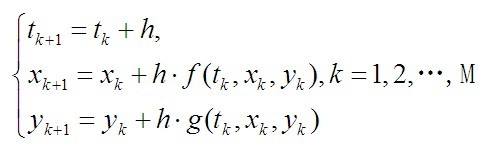
提高精度，得到4价Runge-Kutta Method:

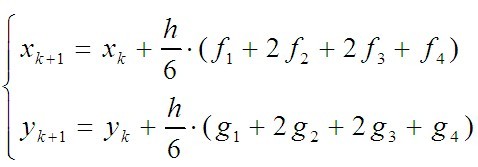
其中：

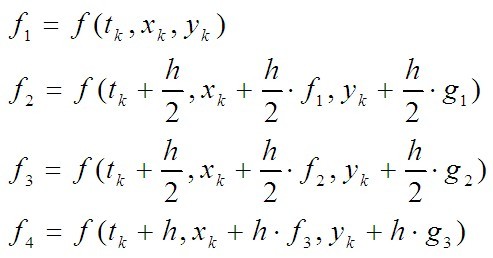
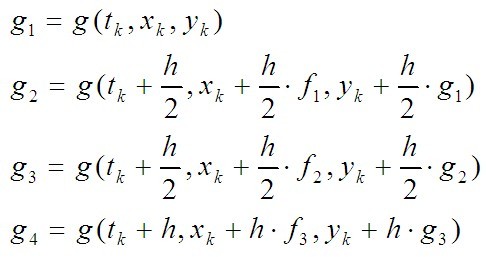
下面是程序：
function E=euler(f,g,a,b,xa,ya,M)
%Input - f is the function entered as a string 'f'
%      - g is the function entered as a string 'g'
%         - a and b are the left and right endpoints
%         - xa is the initial condition x(a)
%         - ya is the initial condition y(a)
%         - M is the number of steps
%Output - E=[T' X' Y'] where T is the vector of abscissas 
%              and X and Y are the vectors of ordinates
h=(b-a)/M;
T=zeros(1,M+1);
X=zeros(1,M+1);
Y=zeros(1,M+1);
T=a:h:b;
X(1)=xa;
Y(1)=ya;
for j=1:M
X(j+1)=X(j)+h*feval(f,T(j),X(j),Y(j));
Y(j+1)=Y(j)+h*feval(g,T(j),X(j),Y(j));
end
E=[T' X' Y'];

 

function H=heun(f,g,a,b,xa,ya,M)
%Input    - f is the function entered as a string 'f'
%         - g is the function entered as a string 'g'
%             - a and b are the left and right endpoints
%             - xa is the initial condition x(a)
%             - ya is the initial condition y(a)
%             - M is the number of steps
%Output - H=[T' X' Y'] where T is the vector of abscissas
%                and X and Y are the vectors of ordinates
h=(b-a)/M;
T=zeros(1,M+1);
X=zeros(1,M+1);
Y=zeros(1,M+1);
T=a:h:b;
X(1)=xa;
Y(1)=ya;
for j=1:M
    k1=feval(f,T(j),X(j),Y(j));
    k2=feval(g,T(j),X(j),Y(j));
    k3=feval(f,T(j+1),X(j)+h*k1,Y(j)+h*k2);
    k4=feval(g,T(j+1),X(j)+h*k1,Y(j)+h*k2);
    X(j+1)=X(j)+(h/2)*(k1+k3);
    Y(j+1)=Y(j)+(h/2)*(k2+k4);
end
H=[T' X' Y'];

 

function R=rk4(f,g,a,b,xa,ya,M)
%Input    - f is the function entered as a string 'f'
%         - g is the function entered as a string 'g'
%             - a and b are the left and right endpoints
%             - xa is the initial condition x(a)
%             - ya is the initial condition y(a)
%             - M is the number of steps
%Output -R=[T' X' Y'] where T is the vector of abscissas
%              and X and Y are the vectors of ordinates
h=(b-a)/M;
T=zeros(1,M+1);
X=zeros(1,M+1);
Y=zeros(1,M+1);
T=a:h:b;
X(1)=xa;
Y(1)=ya;
for j=1:M
    k1=h*feval(f,T(j),X(j),Y(j));
    k2=h*feval(g,T(j),X(j),Y(j));
    k3=h*feval(f,T(j)+h/2,X(j)+k1/2,Y(j)+k2/2);
    k4=h*feval(g,T(j)+h/2,X(j)+k1/2,Y(j)+k2/2);
    k5=h*feval(f,T(j)+h/2,X(j)+k3/2,Y(j)+k4/2);
    k6=h*feval(g,T(j)+h/2,X(j)+k3/2,Y(j)+k4/2); 
    k7=h*feval(f,T(j)+h,X(j)+k5,Y(j)+k6);
    k8=h*feval(g,T(j)+h,X(j)+k5,Y(j)+k6);
    X(j+1)=X(j)+(k1+2*k3+2*k5+k7)/6;
    Y(j+1)=Y(j)+(k2+2*k4+2*k6+k8)/6;
end
R=[T' X' Y'];

由于前面的原理介绍已经比较清楚了，所以程序中的计算就不赘述了

 

下面是M文件的截图：

 

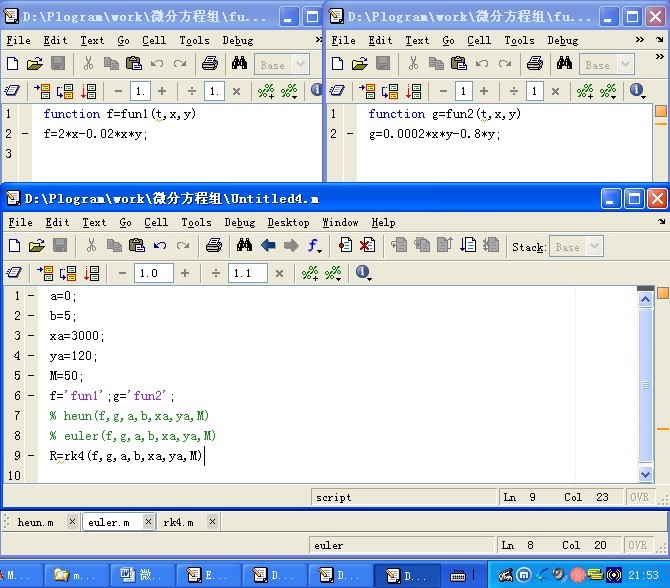
部分解释：

 

 

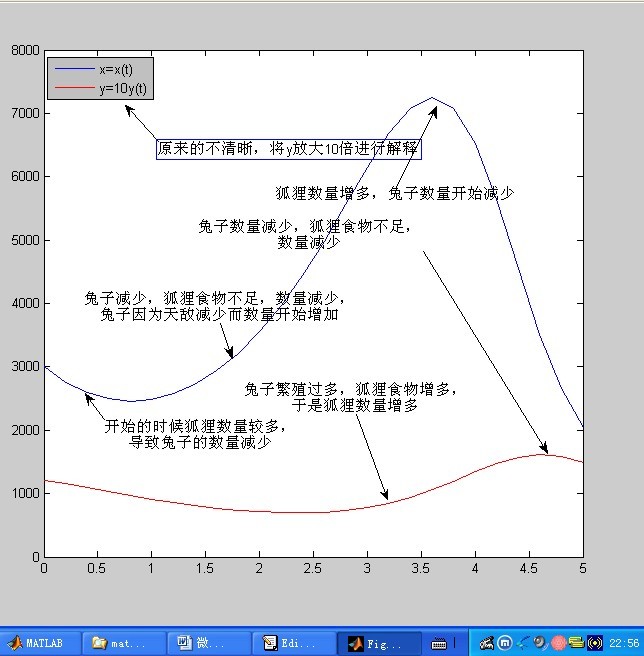
下面在同一个图中作出Euler,Heun,Runge-Kutta Method 对应的y-x图象：

 

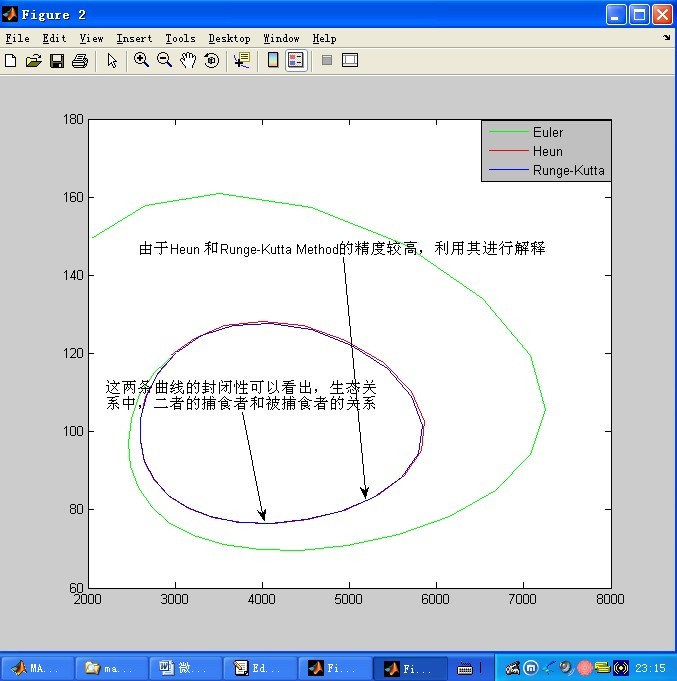
既然看出二者在同一个图中表示的是一条封闭曲线，说明了生态系统的自我调节过程，揭示了捕食者和被捕食者的在数量上的动态关系，图象的闭合性也说明了模型的正确性：具有周期性、在周期内的数量呈现振荡关系，一段时间内此消彼长，一段时间内，共同增加，但是增长率随着一方数量的增加而减小。具体的说，在捕食者和被捕食者模型中临界点为(D/C,A/B)=(4000,100)，并且知道这个临界点是中心。可以参考上图。初值条件X0越靠近(4000,100),周期解就越像相应线性方程组的椭圆解。g’((4000,100))的特征值为λ=±√(AD)*i=±2/5*√10i,所以周期为(√10)π/2,或者约等于4.97

 

总结：

可以看到,这个模型中，Heun Method 和Runge-Kutta Method对模型的拟合程度较高，精度也比Euler Method 高，从纵向比较，我们可以看出，随着步长的减小，Euler Method，Heun Method 和Runge-Kutta Method的精度提高。

这里，仍然有必要对x=x(t)和y=y(t)图象进行总的说明：

兔子和狐狸的数量在一开始的时候，由于狐狸的数量超过生态系统中的数量（换句话说，就是兔子的数量满足不了狐狸的需求），狐狸在一段时间内，由于食物缺乏而死亡，兔子由于过多狐狸的捕食而减少数量，当狐狸的数量减少到一定程度时，兔子由于天敌的减少而不断繁殖，于是数量增加，狐狸自身减少的同时，由于食物的增加，于是渐渐的食物充足而开始不断繁殖；狐狸不断繁殖，导致兔子的增长率减小，达到一定的程度时，兔子的数量满足不了狐狸的需求，狐狸开始减少，于是这样的周而复始……

对于y-x图象，前面已经说过，这是一条封闭的曲线，封闭性同说明了生态系统的自我调节过程，揭示了捕食者和被捕食者的在数量上的动态关系，图象的闭合性也说明了模型的正确性：具有周期性、在周期内的数量呈现的振荡关系：一段时间内此消彼长，一段时间内，共同增加――恰恰从另一个方面说明了x(t)-t,y(t)-t,的关系。

必须再次强调的是

在捕食者和被捕食者模型中临界点为(D/C,A/B)=(4000,100)，并且知道这个临界点是中心。初值条件X0越靠近(4000,100),周期解就越像相应线性方程组的椭圆解。g’((4000,100))的特征值为λ=±√(AD)*i=±2/5*√10i,所以周期为(√10)π/2,或者约等于4.97。

 

欢迎前往个人博客 驽马点滴 和视频空间 哔哩哔哩-《挨踢日志》