题意:给出一个三角形ABC的三条边长,求DEF的面积和阴影部分总面积。
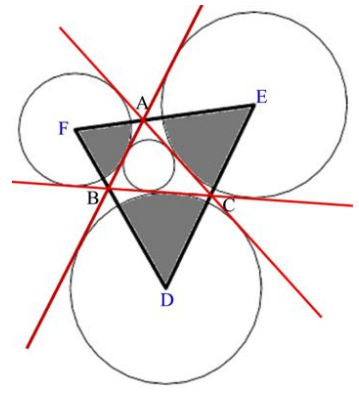
题解:三角形内部的圆是内切圆,而外面的三个圆是旁切圆,关于旁切圆有一个性质就是他的圆心是三角形两个外角的角平分线(比如AF和BF)和一条内角平分线(CF)的交点,由此可以推出∠EAC == ∠FAB,∠FBA == ∠CBD,∠BCD == ∠ACE。
然后可以推导出下列三个式子:
∠EAC + ∠E + ∠ACE = 180°
∠EAC + ∠F +∠FBA = 180°
∠FBA + ∠D + ∠ACE = 180°
上面三个式子相加推出 ∠FBA == ∠E
因为∠FAB == ∠EAC 且 ∠FBA == ∠E
那么△AFB和△ACE是相似三角形,同理推出 △BCD和他们也是相似的
现在已知△ABC三边长度,根据余弦定理可以得出所有角的大小,然后根据正弦定理计算所有边的长度,△DEF就很容易计算出来了。
阴影部分是三个扇形面积的和,扇形面积 S = n * π * r * r / 360°,n是圆心角的角度,r是半径。因为旁切圆和三角形相切,那么有了面积和底边长度,半径其实是三个小三角形的高。然后角度都已知,直接三个小扇形计算累加就是阴影部分的总面积。
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const double PI = acos(-1);
double a, b, c;
// ACE AFB DCB 相似
int main() {
int cas = 1;
while (scanf("%lf%lf%lf", &a, &b, &c) == 3 && a + b + c) {
double bac = acos((b * b + c * c - a * a) / (2 * b * c));
double abc = acos((c * c + a * a - b * b) / (2 * c * a));
double bca = acos((a * a + b * b - c * c) / (2 * a * b));
double d = (PI - bac) / 2.0;
double f = (PI - bca) / 2.0;
double e = (PI - abc) / 2.0;
double BF = c * sin(d) / sin(f);
double AF = c * sin(e) / sin(f);
double BD = a * sin(f) / sin(d);
double CD = a * sin(e) / sin(d);
double AE = b * sin(f) / sin(e);
double CE = b * sin(d) / sin(e);
double Sdef = 0.5 * (AF + AE) * (BD + BF) * sin(f); //1/2 * a * b * sin(C)
printf("Case %d: %.2lf", cas++, Sdef);
double Sabf = 0.5 * AF * BF * sin(f);
double r1 = Sabf * 2.0 / c;
double S1 = f * r1 * r1 / 2.0;//注意弧度转化成角度,这是式子化简后的样子
double Sbcd = 0.5 * BD * CD * sin(d);
double r2 = Sbcd * 2.0 / a;
double S2 = d * r2 * r2 / 2.0;
double Sace = 0.5 * AE * CE * sin(e);
double r3 = Sace * 2.0 / b;
double S3 = e * r3 * r3 / 2.0;
printf(" %.2lf\n", S1 + S2 + S3);
}
return 0;
}





















 716
716

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








