Algorinote_10_主定理与 Akra-Bazzi 定理
主定理 Master theorem
对于形如 T ( n ) = a T ( n b ) + f ( n ) T(n)=aT(\frac nb)+f(n) T(n)=aT(bn)+f(n) 的递归式,其中:
- n 是问题规模大小;
- a 是原问题的子问题个数;
- n/b 是每个子问题的大小,这里假设每个子问题有相同的规模大小;
- f(n) 是将原问题分解成子问题和将子问题的解合并成原问题的解的时间。
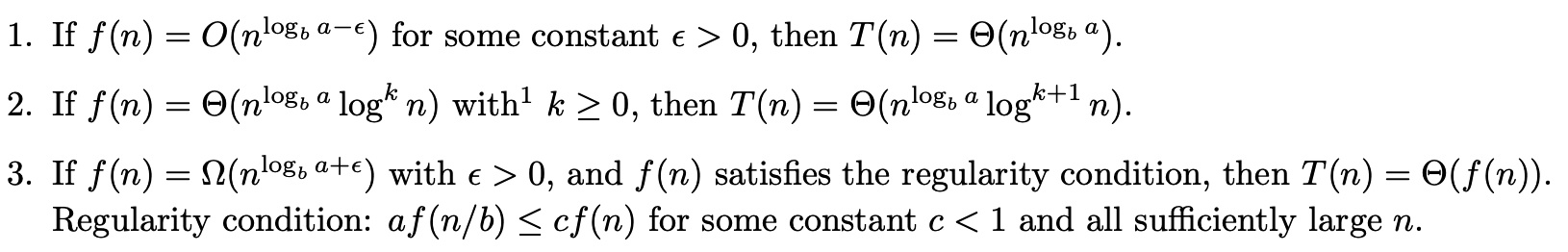
令 d 是 f(n) 中 n 的最高幂次, f ( n ) = Θ ( n d ) f(n)=\Theta(n^d) f(n)=Θ(nd)。
拿 f ( n ) f(n) f(n) 与 n log b a n^{\log_ba} nlogba 的增长速度进行对比,原理上是在每层的单个子问题的治理时间 a l a y e r a^{layer} alayer,与子问题的数量之间作权衡 b d ∗ l a y e r b^{d\ *\ layer} bd ∗ layer(具体证明可以看看下文),实际是比较 d − log b a d - \log_ba d−logba 或 a − b d a - b^d a−bd 。于是有:
- 如果后者更大,则 T ( n ) = Θ ( n l o g b a ) T(n)=\Theta(n^{log_ba}) T(n)=Θ(nlogba)
- 如果二者相等,则 T ( n ) = Θ ( n log b a log k + 1 n ) = Θ ( n d log n ) T(n)=\Theta(n^{\log_ba}\log^{k+1}n)=\Theta(n^d\log n) T(n)=Θ(nlogbalogk+1n)=Θ(ndlogn)
- 如果前者更大,则
T
(
n
)
=
Θ
(
n
d
)
T(n)=\Theta(n^d)
T(n)=Θ(nd)
- 注意还需要对充分大的 n,存在 c < 1 使 a f ( n b ) ≤ c f ( n ) af(\frac nb) \le cf(n) af(bn)≤cf(n)
其中第二点中,因为在对 f ( n ) f(n) f(n) 的分析时得到的通常都是多项式 n d n^d nd 形式,即原文所提到的 log k n \log^kn logkn 形式一般都是 k=0,所以我们把第二点化简成 i f f ( n ) = Θ ( n log b a ) if\ \ f(n)=\Theta(n^{\log_ba}) if f(n)=Θ(nlogba),也就是 d = log b a d = \log_ba d=logba
应用
认真理解一下 T ( n ) = a T ( n b ) + f ( n ) T(n)=aT(\frac nb)+f(n) T(n)=aT(bn)+f(n),a 代表当前层的分支数,f(n) 代表分支前的耗时,也就是本层用时,b 代表分解时对当前问题的切分程度,也即子问题与母问题的比例。
所以对于我们熟悉的快速排序,有 T ( n ) = 2 T ( n 2 ) + O ( n ) T(n)=2T(\frac n2)+O(n) T(n)=2T(2n)+O(n),所以 d = 1 = log 2 2 = 1 d=1 = \log_22=1 d=1=log22=1, T ( n ) = Θ ( n log n ) T(n)=\Theta(n\log n) T(n)=Θ(nlogn)
证明

根据对递归式的理解,第 i i i层有 a i a^i ai个子问题,每个子问题的大小是 n / b i n / b^i n/bi
所以这一层的用时是 a i ⋅ O ( ( n b i ) d ) = O ( n d ) ⋅ ( a b d ) i a^i \cdot O((\frac{n}{b^i})^d) = O(n^d)\cdot(\frac{a}{b^d})^i ai⋅O((bin)d)=O(nd)⋅(bda)i
把每层用时累加起来就是 KaTeX parse error: Expected group after '_' at position 5: \sum_̲\limits{i=0}^{\…,可以看出是一个等比数列,公比 q = a b d q=\frac{a}{b^d} q=bda ,考虑对 q 进行分类讨论(省略化简过程)
- q > 1,即 d < log b a d < \log_ba d<logba,最后一项占主导, S = O ( O ( n d ) ( a b d ) log b a ) = O ( n log b a ) S=O(O(n^d)(\frac{a}{b^d})^{\log_ba})=O(n^{\log_ba}) S=O(O(nd)(bda)logba)=O(nlogba)
- q = 1,全都一样大,求和 S = ( 1 + log b a ) O ( n d ) = O ( n d log n ) S=(1+\log_ba)O(n^d)=O(n^d\log n) S=(1+logba)O(nd)=O(ndlogn)
- q < 1,即
d
>
log
b
a
d > \log_ba
d>logba,第一项占主导,
S
=
O
(
O
(
n
d
)
⋅
1
)
=
O
(
n
d
)
S=O(O(n^d)\cdot1)=O(n^d)
S=O(O(nd)⋅1)=O(nd)
- 此时当 f(n) 不是 n 的简单次幂形式(含有 log)时,还需要考虑 a f ( n b ) ≤ c f ( n ) af(\frac nb) \le cf(n) af(bn)≤cf(n) 来保证序列增长级递减
Akra-Bazzi 定理
考虑形如 T ( x ) = ∑ i = 1 k a i T ( b i x + h i ( x ) ) + f ( x ) , f o r x ≥ x 0 T(x)=\sum\limits_{i=1}^{k}a_iT(b_ix+h_i(x))+f(x),\ \ for\ x\ge x_0 T(x)=i=1∑kaiT(bix+hi(x))+f(x), for x≥x0 的递归式(T的转移可以有更多部分),其中:
- $a_i>0, 0<b_i<1 $
- ∣ g ( x ) ∣ ∈ O ( x c ) , 其 中 c 是 常 数 |g(x)|\in O(x^c),其中c是常数 ∣g(x)∣∈O(xc),其中c是常数
- ∣ h i ( x ) ∣ ∈ O ( x log 2 x ) |h_i(x)|\in O(\frac{x}{\log^2x}) ∣hi(x)∣∈O(log2xx)
则有 T ( x ) = Θ ( x p + x p ⋅ ∫ 1 x f ( u ) u p + 1 d u ) \Large T(x) = \Theta(x^p + x^p\cdot\int_{1}^{x} \frac{f(u)}{u^{p+1}}du) T(x)=Θ(xp+xp⋅∫1xup+1f(u)du),其中 ∑ i = 1 k a i b i p = 1 \sum\limits_{i=1}^{k}a_ib_i^p=1 i=1∑kaibip=1
应用
例题1 T ( n ) = 7 4 T ( 1 2 n ) + T ( 3 4 n ) + n 2 T(n)=\frac 74 T(\frac 12 n)+T(\frac 34n)+n^2 T(n)=47T(21n)+T(43n)+n2
先找 p: 7 4 ( 1 2 ) p + ( 3 4 ) p = 1 \frac 74(\frac 12)^p+(\frac 34)^p = 1 47(21)p+(43)p=1,解得 p=2
所以 T ( x ) = Θ ( x 2 ( 1 + ∫ 1 x u 2 u 3 d u ) ) = Θ ( x 2 ( 1 + log x ) ) = Θ ( x 2 log x ) T(x) = \Theta(x^2 (1+\int_{1}^{x} \frac{u^2}{u^{3}}du))=\Theta(x^2(1+\log x))=\Theta(x^2\log x) T(x)=Θ(x2(1+∫1xu3u2du))=Θ(x2(1+logx))=Θ(x2logx)
例题2 T ( n ) = 1 4 T ( 3 4 n ) + 3 4 T ( 1 4 n ) + 1 T(n)=\frac 14 T(\frac 34 n)+\frac 34 T(\frac 14n)+1 T(n)=41T(43n)+43T(41n)+1
显然 p=0, T ( x ) = Θ ( 1 + ∫ 1 x 1 u d u ) = Θ ( log x ) T(x)=\Theta(1+\int_1^x\frac 1udu)=\Theta(\log x) T(x)=Θ(1+∫1xu1du)=Θ(logx)
Ref
https://zhuanlan.zhihu.com/p/100531135
https://my.oschina.net/u/4324616/blog/4778589
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








