IEEE754-2008 标准详解(三)：十进制交换格式编码

IEEE754-2008 标准详解(三)：十进制交换格式编码

---

本文为原创文章，转载请注明出处，并注明转载自“黄邦勇帅(原名：黄勇)”
本文是对《C++语法详解》一书相关章节的增补，以增强读者对浮点数的理解，原书引用的是老版的 IEEE754-1985 标准

《C++语法详解》网盘地址：https://pan.baidu.com/s/1dIxLMN5b91zpJN2sZv1MNg

本文摘自本人所作《IEEE754-2008标准详解》网盘地址
链接：https://pan.baidu.com/s/10soDctgCJ84MDs3PyhJBcw?pwd=lzku
提取码：lzku

有兴趣的读者可参阅本人所著《C++语法详解》一书，电子工业出版社出版，该书语法示例短小精悍，对查阅C++知识点相当方便，并对语法原理进行了透彻、深入详细的讲解，可确保读者彻底弄懂C++的原理，彻底解惑C++，使其知其然更知其所以然。此书是一本全面了解C++不可多得的案头必备图书。

由于本人能力有限，文中难免有错漏之处，望广大读者指出更正，不胜感激

---

3.1 十进制交换格式编码的格式

---

3.1.1、讲解之前的说明

1、十进制交换格式编码是对十进制浮点数据的编码方法，因此，在编码之前，应使用真实十进制浮点数据，其中基数必须是10，尾数可以是二进制也可以是十进制，

2、十进制编码的真实浮点数据应使用形式为 (−1)^s × c × b^q 的指数表示法，需要注意的是此处的尾数c是整数。

3.1.2、十进制交换格式编码各字段详解

1、与二进制编码相同，IEEE 754同样把浮点数据的编码分为3个字段(或部分)，即：

• 一位符号位S

• w+5位组合字段G，
  当编码数据是一个有限数时，则G是由指数q和有效数(即尾数c)的编码组合而成的，也就是说字段G当中既含有指数q的编码也含有尾数的编码，注：G中只含有部分尾数的编码，详见后文。

• t位末尾有效数字段T，
  该字段仅包含大部分尾数c的编码(注意：并未包含c的全部编码)，其中

  t = J × 10 //公式3.1

  当字段T与组合字段G中的尾数c的编码组合时，总共可编码

  p = 3 × J + 1 //公式3.2

  位十进制数字

• w+2位偏移指数E
  E= q + bias，其前两位合起来(taken together)的值为0，1或2，也就是说，前两位不能同时为1，因为，若同时为1，则其值为3了。

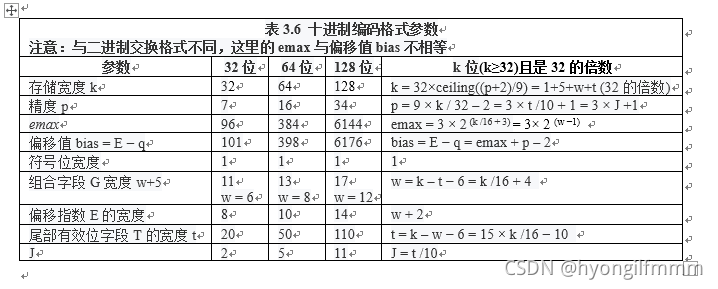
2、图XXX显示了十进制编码的格式，图中同时给出了float、double各字段所占的宽度。通常float型使用总宽度32位存储，而double使用64位总宽度存储。注：总宽度就是指的存储宽度，使用k表示。

3、当k是32的正数倍时，各参数可使用以下公式计算，注：ceiling()表示向上取整。

k = 1 + 5 + w + t = 32 × ceiling(( p + 2) /9)
w = k – t − 6 = k /16 + 4
t = k – w − 6 = 15 × k /16 − 10
p = 3 × t /10 + 1 = 9 × k /32 − 2
emax = 3 × 2 ^(w−1) //公式3.3
emin = 1 − emax //公式3.4
bias = emax + p − 2 //公式3.5

4、注意以下问题

• 十进制编码格式中，q是真实指数，c是尾数且是整数，字段T中的编码不再是二进制编码格式时的小数部分的原码(具体编码规则见后文)

5、表XXX给出了十进制编码格式各参数的取值

---

3.2 十进制交换格式的编码规则

---

3.2.1、指数的编码规则

1、十进制交换格式的真实指数q，仍然使用偏移指数来编码，其偏移值的公式是

bias = E − q = emax + p – 2 //公式3.6

其中

emax = 3 × 2 (k /16 + 3) = 3 × 2 ^(w−1) //公式3.7

偏移指数E的公式为

E = q + bias = q + emax + p – 2 (占w+2位) //公式3.8

比如，对于float型p = 7，k = 32， bias = 101，emax = 96

2、因为E的具体编码规则比较复杂，见后文。

3.2.2、编码前的一些说明

1、十进制交换格式不再像二进制交换格式一样，将相应的数转换为二进制后依次编码在相应的字段即可，十进制交换格式使用的是另一种编码规则。

2、为讲解方便，本文引入如下书写规则

• 偏移指数使用下标形式指明所在的位(从最高位0开始)，如E₀表示偏移指数第1位。
• 使用不带下标的字母表示该类型的所有位，如
  • E = 0，表示E的所有位都编码为0，注意，E所占的位置并不一定是连续的。
  • c = G_w+2 ~ G_w+4 ⋃ T ，表示c的编码由G_w+2 ~ G_w+4 和 T的所有位组成。
  • c = G₄ ⋃ T，表示c的编码由G₄和T的所有位组成

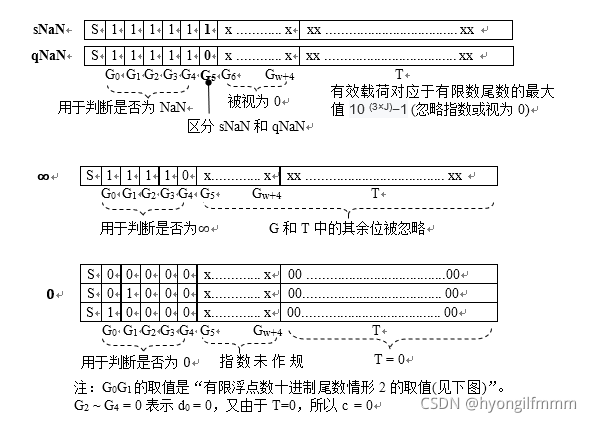
3.2.3、NaN、∞的编码规则

1、NaN

• 若G₀G₁G₂G₃G₄ = 11111，则无论S如何，该数都为NaN，若G₅ = 1，则是sNaN，否则为qNaN

• NaN的有效载荷(payload)编码于末尾有效数字段，类似于将G的所有位都视为0时(也可理解为忽略指数字段)，具有以下最大值的整数，即，编码后的有效载荷对应的整数值的最大值为以下数：

  payload ≤ 10 ^(3×J)−1 (全为9) //公式3.9

  即，全为9，比如float，payload ≤10 ^(3×J)−1 = 10 ^(3×2)−1 = 99999

• 若G₆到G_w+4的位全是0，且有效载荷的编码是规范的(canonical)，则这个NaN就是它的规范(首选)表示法

2、∞

• 若G₀G₁G₂G₃G₄ = 11110，则该数是无穷大，G和T中的其余位被忽略，此时的真实浮点数据为
  v = (−1) _S × (+∞)
• 有两种无穷大的规范表示法，即G₅到G_w+4 为0和T = 0，

3.2.4、有限浮点数的编码规则

1、当十进制交换格式表示的是有限浮点数时，其真实浮点数据的公式为

v = (−1) ^S × c × 10 ^(E−bias)

其中c是由字段T和字段G组合而成的，此时的偏移指数E被编码在字段G中。其具体的编码规则取决于实现对于尾数c是使用十进制编码还是二进制编码。

2、当实现对尾数c使用十进制编码时

• 1)、低位的编码

  • 指数的最低有效的w位是G₅ ~ G_w+4 (注：指数占据w + 2位)，即

    E₂ ~ E_w+1 = G₅ ~ G_w+4 //公式3.10

  • c的p−1位(即d₁…d_p-1)由T组成，使用densely-packed decimal编码方式编码(详见后文)

• 2)、高位的编码
  E的最高两位和c的最高有效位d₀由以两种方式之一编码，具体使用哪种方式需根据真实数的最高位d₀是否大于等于7来判断

  • 情形1：当G₀ ~ G₄ = 110xx或1110x时(注意：G₂G₃ ≠ 11)

    • E的最高两位为

      E₀E₁ = 2G₂ + G₃ = G₂ × 2¹ + G₃ ×2⁰

      其值为0，1或2 (注意：不能等于3，这说明G₂、G₃不能同时为1)

    • c的前导有效数d₀为

      d₀ = 8 + G₄

      其值为8或9

    • 最终编码的结果为

      E = E₀ ~ E_w+1 = G₂G₃ ⋃ G₅ ~ G_w+4 (共w+2位) //公式3.11
      c = d₀ ~ d_p−1 = G₄ ⋃ T (共t + 1位) //公式3.12

  • 情形2：当G₀ ~ G₄ = 0xxxx或10xxx时，(注意：G₀G₁ ≠ 11)

    • E的最高两位为

      E₀E₁ = 2G₀ + G₁ = G₀ × 2¹ + G₁ ×2⁰

      其值为0，1或2 (注意：不能等于3，这说明G₀、G₁不能同时为1)

    • c的前导有效数d₀为

      d₀ = 4G₂ + 2G₃ + G₄ = G₂ × 2² + 2G₃ × 2¹ + G₄ × 2⁰

      其值为0 ~ 7

    • 最终编码的结果为

      E = E₀ ~ E_w+1 = G₀G₁ ⋃ G₅ ~ G_w+4 (共w+2位) //公式3.13
      c = d₀ ~ d_p−1 = G₂G₃G₄ ⋃ T (共t + 1位) //公式3.14

    • 0的编码
      因此，若此时T = 0，且G₀ ~ G₄为00000、01000或10000时(此时属情形2，可见，d₀ = 0)，该数为0，其真实浮点数据为v = (−1) ^S × (+0)
      注意：并未指明E是否需要为0

  • 可把以上两种情形综合理解为

    • 只要G₀ ~ G₃(前4位)不全为1时即为有限数
    • 尾数c的最高位d₀被编码在字段G中，有可能使用1位或3位来编码d₀
    • 指数q全部编码在字段G中，但不一定是连续的。

3、当实现对尾数c使用二进制编码时
注：二进制编码有个重要的问题，IEEE754并没有指定“实现”使用何种方式的二进制编码，如十进制尾数可使用BCD编码，2421编码，压缩十进制编码或者其他编码等多种编码方式

• 1)、情形1：
  当G₀G₁是00、01、10中的一个时(注意：G₀G₁ ≠ 11)

  E = G₀ ~ G_w+1 ==//公式3.15 ==
  c = G_w+3 ~ T //公式3.16

• 2)、情形2：
  当G₀G₁ = 11，G₂G₃为00、01、10时(注意：G₂G₃ ≠ 11)

  E = G₂ ~ G_w+3 //公式3.17
  c 由 8 + G_w+4 和 T形成 //公式3.18

• 3)、可把以上两种情形综合理解为只要G₀ ~ G₃(前4位)不全为1时即为有限数

4、二进制编码尾数的最大值与对应的十进制编码尾数的最大值相同，即，都为

10 ^(3×J+1)−1 (或10 ^(3×J)−1，当T用作NaN的有效载荷时)

如果该值超过最大值，则有效数c是非规范的，且用于c的值为零。

5、图XXX分别为NaN、∞、0和有限浮点数编码的图示表示

3.2.5、densely-packed decimal编码

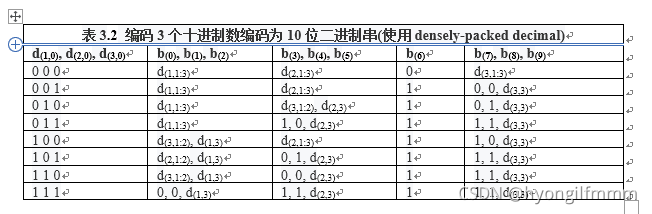
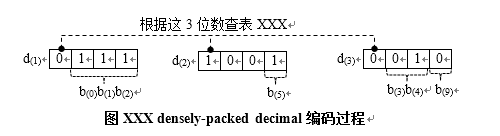
1、表3.2将3个十进制数d₍₁₎、d₍₂₎、d₍₃₎编码为10位二进制串 ( b₍₀₎到b₍₉₎ )，其中每个十进制数各有4位二进制串，可以通过如下所示的第二个下标表示

d_(1,0:3)、d_(2,0:3)、d_(3，0:3)
其中0:3中的0是最高位，3是最低位，d_(3，0:3)是指的d₍₃₎的第0 ~ 3位(从高到低)。
如，789，则
d₍₁₎ = 7 = 0111₂，d₍₂₎ = 8 = 1000₂，d₍₃₎ = 9 = 1001₂
d_(3,1:3) = 001，d_(3,3) = 1
其中d_(3,1:3)是指的d₍₃₎的1 ~ 3位(从高到低)，d_(3,3)是指的d₍₃₎的第3位(从高到低)
计算运算(什么是计算运算详见后文)仅生成表XXX定义的1000个规范的(canonical )10位模式。

2、IEEE 754把使用densely-packed decimal编码后的10位二进制串称为“declet”。

3、表3.3将10位二进制串b₍₀₎到b₍₉₎ (即delcet)解码为3个十进制数d₍₁₎、d₍₂₎、d₍₃₎ 其中x表示任意的。因此，所有1024个可能的10位模式都必须被接受，并映射为1000个可能的3个位数(3-digit)组合，并具有一定的冗余。

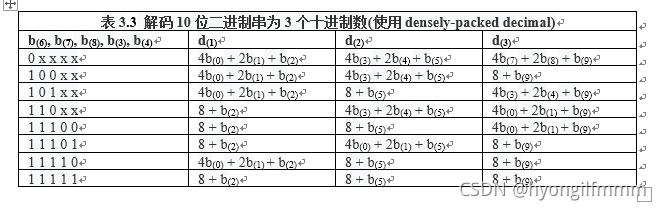
在计算运算的结果中不会生成01x11x111x、10x11x111x或11x11x111x(其中“x”表示“不在乎(don’t care)”位)等24种非规范(non-canonical)模式。然而，如上表3.3所示，这些24位模式确实映射到0到999范围内的值。NaN末尾有效数字段中的位模式会影响NaN的传播方式(详见后文)。

4、示例1：使用densely-packed decimal编码数字792，然后再解码该编码

解：编码过程

d₍₁₎ = 7 = 0111₂，d₍₂₎ = 9 = 1001₂，d₍₃₎ = 2 = 0010₂
根据d_(1,0)d_(2,0)d_(3,0) = 010查表3.2得
b₍₀₎b₍₁₎b₍₂₎ = d_(1,1:3) = 111，
b₍₃₎b₍₄₎b₍₅₎ = d_(3,1:2)d_(2,3) = 011 ,
b₍₆₎ = 1，
b₍₇₎b₍₈₎b₍₉₎ = 01d_(3,3) = 010
因此 752 = b₍₀₎ ~ b₍₉₎ = 111 011 1 010

图XXX为densely-packed decimal编码过程

解码过程

b₍₀₎ ~ b₍₉₎ = 111 011 1 010

根据b₍₆₎b₍₇₎b₍₈₎b₍₃₎b₍₄₎ = 10101查表3.3得
d₍₁₎ = 4b₍₀₎ + 2b₍₁₎ + b₍₂₎ = 4×1+2×1+1 = 7
d₍₂₎ = 8 + b₍₅₎ = 9
d(3) = 4b₍₃₎ + 2b₍₄₎ + b₍₉₎ = 4×0 + 2×1 + 1×0 = 2
因此b₍₀₎ ~ b₍₉₎ = 111 011 1 010 = 792

3.2.6、十进制交换格式编码和解码示例

**示例：**将数字7.92452×10⁸⁵编码后再解码，假设使用32位存储，尾数使用十进制编码

编码过程
1、查表XXX，得到32位宽度的十进制交换格式的各参数分别为

p = 7，bias = 101，w = 6，t = 20，J = 2，E占8位，G占11位

2、将尾数化为整数，由于p =7，因此，尾数需保留7位数，即

7.924×10⁸⁵ = 7924520 × 10⁷⁹

3、判断使用哪种10进制情形，
由于d₀ = 7，所以应使用情形2编码，即，组合字段G的最高5位G₀ ~ G₄ = 0xxxx或10xxx的情形

4、编码指数
偏移指数E = e + bias = 79 +101 = 180 = 1011 01002 ，由于
E = E₀ ~ E₇ = G₀G₁ ⋃ G₅ ~ G₁₀ ，
所以

G₀G₁ = E₀E₁ = 10
G₅ ~ G₁₀ = E₂ ~ E₇ = 11 0100

5、编码尾数的最高位d₀
由于d₀ = 4G₂ + 2G₃ + G₄ = 7 ，因此，

G₂G₃G₄ = 111

6、至此，组合字段G的编码为

G = G₀ ~ G₁₀ = 10111 110100

7、编码尾数的低位d₁ ~ d₆ = 924520

• 1)、编码d₁d₂d₃ = 924
  需要使用densely-packed decimal编码

  d₍₁₎ = 9 = 1001₂，d₍₂₎ = 2 = 0010₂，d₍₃₎ = 4 = 0100₂
  根据d_(1,0)d_(2,0)d_(3,0) = 100查表3.2得
  b₍₀₎b₍₁₎b₍₂₎ = d_(3,1:2)d_(1,3) = 101
  b₍₃₎b₍₄₎b₍₅₎ = d_(2,1:3) = 010
  b₍₆₎ = 1
  b₍₇₎b₍₈₎b₍₉₎ = 10d_(3,3) = 100
  因此 924 = b₍₀₎ ~ b₍₉₎ = 10 1010 1100

• 2)、编码d₄d₅d₆ = 520

  d₍₁₎ = 5 = 0101₂，d₍₂₎ = 2 = 0010₂，d₍₃₎ = 0 = 0000₂

  注意：不带括号的下标表示的是真实数据某位的数字，而带括号的下标是指的用于densely-packed decimal编码时使用的数字，二者不要混淆了。如，d₄表示的是真实浮点数据的第4位(从0开始计算)，而d₍₁₎表示的是使用densely-packed decimal编码时的第一个十进制数字(范围为1~3)

  根据d_(1,0)d_(2,0)d_(3,0) = 000查表3.2得
  b₍₀₎b₍₁₎b₍₂₎ = d_(1,1:3) = 101
  b₍₃₎b₍₄₎b₍₅₎ = d_(2,1:3) = 010
  b₍₆₎ = 0
  b₍₇₎b₍₈₎b₍₉₎ = d_(3,1:3) = 000
  因此 520 = b₍₀₎ ~ b₍₉₎ = 10 1010 0000

• 3)、所以T =924520 = 10 1010 1100 10 1010 0000

8、符号位S = 0

9、所以，最终编码为
S + G + T = 0 10111 110100 10 1010 1100 10 1010 0000 (如下图所示)

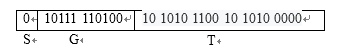
10、注：理论上来讲，以上编码过程也可将原数转换为

7.924×10⁸⁵ = 792452 × 10⁸⁰ = 0792452 × 10⁸⁰

的形式来编码(即，在高位补0的方式)，此时c的最高位d₀ = 0，读者可自行按此方式编码(注：IEEE754并未讲清楚具体应该使用前面补0还是后面补0的方式)。至于为什么会有多种情形编码，详见后文对“队列”的讲解。

解码过程

0 10111 110100 10 1010 1100 10 1010 0000

1、由于G₀ ~ G₄ = 10111，属于尾数是十进制编码的情形2

2、解码指数
由于G₀G₁ =10，G₅ ~ G₁₀= 11 0111，因此
E = E₀ ~ E₇ = G₀G₁ + G₅ ~ G₁₀ = 1011 0100 = 180
因此，真实指数

q = E − bias = 180 − 101 = 79

3、解码尾数

• 1)、解码尾数的最高位d₀

  d₀ = 4G2 + 2G3 + G4 = 7

• 2)、解码尾数的其他位
  由于，T = 10 1010 1100 10 1010 0000
  T的高10位为10 1010 1100

  根据b₍₆₎b₍₇₎b₍₈₎b₍₃₎b₍₄₎ = 110 01查表3.3得到
  d₍₁₎ = 8 + b₍₂₎ = 8 + 1 = 9
  d₍₂₎ = 4b₍₃₎ + 2b₍₄₎ + b₍₅₎ = 0 + 2 + 0 = 2
  d₍₃₎ = 4b₍₀₎ + 2b₍₁₎ + b₍₉₎ = 4 + 0 + 0 = 4
  因此，尾数的d₁d₂d₃ = 924

  T的低10位为10 1010 0000

  根据b₍₆₎b₍₇₎b₍₈₎b₍₃₎b₍₄₎ = 000 01查表.3.3得到
  d₍₁₎ = 4b₍₀₎ + 2b₍₁₎ + b₍₂₎ = 4 + 0 + 1 = 5
  d₍₂₎ = 4b₍₃₎ + 2b₍₄₎ + b₍₅₎ = 0 + 2 + 0 = 2
  d₍₃₎ = 4b₍₇₎ + 2b₍₈₎ + b₍₉₎ = 0 + 0 + 0 = 0
  因此，尾数的d₄d₅d₆ = 520

3、因此，尾数c = d₀ ~ d₆ = 7924520

4、符号位S = 0

5、所以，最终解码后的真实浮点数据为

v = (−1) ^S × c × 10 ^q = (−1) ⁰ × 7924520 × 10 ⁷⁹ = 7924520 × 10 ⁷⁹

3.2.7、队列 (chort)

1、十进制浮点格式与二进制浮点格式不同，在十进制浮点格式中，对同一个浮点数可能有多种不同的表示法，这些表示法的集合称为“浮点数的队列(简称队列)”，队列中的表示法称为队列的成员，比如，若c是10的倍数，则(−1) ^S × c × 10 ^q 和 (−1) ^S × c/10 × 10 ^q+1 表示的是相同的浮点数，但他们属于同一列队，(−1) ^S × c × 10 ^q 和 (−1) ^S × c/10 × 10 ^q+1 是队列中的两个成员。

2、队列有一个限制条件，尾数需要是整数，比如，450，45×10 ¹，4500×10 ⁻¹，45000×10 ⁻²，450000 × 10 ⁻³ 都属于同一个队列，他们是表示的同一个数，但尾数必须是整数。

3、对于格式中精度为p的n位数，若该数末尾不含0，且是整数，则最多有

p − n + 1 //公式3.19

个成员，若该数是接近格式指数范围的极端值，则有可能少于p − n + 1个成员。比如，若p = 7，则表示45的队列有p − n +1 = 7 − 2 + 1 = 6个成员，如下所示

45，450 × 10 ⁻¹，4500 × 10 ⁻²，45000 × 10 ⁻³，450000 × 10 ⁻⁴，4500000 × 10⁻⁵

同理，可把尾数含有0的数转换为尾数不含0的形式，从而计算出队列成员的个数仍为p − n +1， 如，450可转换为45 × 10，从而队列的个数为p − 2 +1

4、0有一个更大的队列，+0的队列包含每个指数的表示法，−0的队列也是如此。

3.2.8 十进制交换格式真实指数q的取值范围

1、由公式1.6可知
emin ≤ q + p − 1 ≤ emax
因此，q的取值范围为

emin − ( p − 1) ≤ q ≤ emax − ( p − 1) //公式3.20

注意：q的取值范围并不是 emin ≤ q ≤ emax

2、q的取值范围是能被编码的范围，如下所示：

• 1)、由前文对十进制交换格式编码的讲解可知，有限浮点数无论使用哪种情形，偏移指数E的最大取值都只能为

  E = 10111…111₂ (共w+2位) = 2^w+1 + 2^w −1 = 3 × 2^w−1 = 2 × 3 × 2^w−1 −1

  由于emax = 3 × 2^w−1 ，bias = emax + p – 2 ，
  因此，以上的

  E = 2 × emax −1

  所以，能被编码的有限浮点数的最大指数q为：

  q = E − bias = (2 × emax −1) − (emax + p − 2 ) = emax − (p − 1)

  由此可见，当有限浮点数的真实指数q超过emax − (p − 1)时，将不能被编码，即，有p − 1个真实指数不能被编码，比如，对于32位的十进制交换格式，emax = 96，p = 7，所以，能被编码的有限浮点数的真实指数q的最大值为emax − (p − 1) = 90，当真实指数为91~96时将不能被编码(指数溢出了)。

• 2)、十进制交换格式的编移指数E的最小值可以为0，因此，能被编码的有限浮点数的最小指数q为：

  q = 0 − bias = − emax − p + 2 = 1 − emax − p + 1 = emin − (p − 1)

  由此可见，能被编码的真实指数比最小值emin还要小p−1，如，对于32位的十进制交换格式，emin = −95，p = 7，所以，能被编码的有限浮点数的真实指数q的最小值为emin − (p − 1) = −101，也就是比最小指数−95还要小的指数仍然可以被编码。

3、十进制交换格式真实指数q的取值范围并不位于emin或emax之间的原因，可能与队列有关(注：这是本人个人推测)，如下所示：

• 因为，被编码的有限浮点数的尾数必须表示为p位，因此，若某个p位真实浮点数的指数为emax − (p−1)时，虽然该数的指数不能表示为emax，但他的队列有可能会包含真实指数为emax的成员(也就是说，该数有可能已经达到最大指数了)，比如，当p = 7时，浮点数3000000 × 10⁹⁰，该数的指数为90，该指数小于最大指数96，但他的队列的成员有

  300000×10⁹¹，30000×10⁹²，3000×10⁹³，300×10⁹⁴，30×10⁹⁵，3×10⁹⁶

  其中，成员3×10⁹⁶ 就达到了最大指数emax = 96，这可能是为什么能被编码的指数的最大值为emax − (p−1)的原因之一。所以，类似3×10⁹⁶ 的数，虽不能被直接编码，但可转换为3000000 × 10⁹⁰ 的形式再编码，但类似34 × 10⁹⁶ 的数没法进行转换后再编码，因为若将指数转换为q = 90之后，尾数c的位数超过了7位(尾数溢出)，若将尾数转换为7位，则指数p又超过了90(指数溢出)，仍无法编码。

3.2.9 十进制交换格式下的规约数与非规约数

1、下面我们来按照之前讲解的规约数与非规约数的规则(见第1章)来推导十进制交换格式下的规约数与非规约数，注意：推导时，尾数由m换为c，但仍应使用纯小数形式来推导，并且基数应换为10，指数e换为q。

2、由第1章讲解可知，正规约数的范围为

b ^emin ~ (b−b^1−p) × b ^emax

因此，对于float型，最小和最大的正规约数分别是

b ^emin = 1 × 10⁻⁹⁵ = 1 000 000 × 10⁻¹⁰¹
(b−b^1−p) × b ^emax = (10−10⁻⁶) × 10⁹⁶ = 9.999 999 × 10⁹⁶

float型规约数的取值范围是

1 × 10⁻⁹⁵ ~ 9.999 999 × 10⁹⁶ (1)

或

1 000 000 × 10⁻¹⁰¹ ~ 9 999 999 × 10⁹⁰ (2)

由(1)可见，指数范围刚好是float型的emin~emax之间，但由(2)可见，将尾数转换为整数后，其指数范围就刚好位于可编码的真实指数的范围之内了。

3、由第1章讲解可知，正非规约数的范围为

b ^emin+1−p ~ (1−b^1−p) × b^emin

对于float型，最小和最大的正非规约数分别是

b ^emin+1−p = 1 × 10 ⁻¹⁰¹ = 0.000 001 × 10 ⁻⁹⁵
(1−b1−p) × b emin =(1−10⁻⁶) × 10 ⁻⁹⁵ = 0.999 999 × 10 ⁻⁹⁵ = 999 999 × 10 ⁻¹⁰¹

float型非规约数的取值范围是

0.000 001 × 10 ⁻⁹⁵ ~ 0.999 999 × 10 ⁻⁹⁵ (3)

或

1 × 10 ⁻¹⁰¹ ~ 999 999 × 10 ⁻¹⁰¹ (4)

由(4)可见，当向左补0以达到p位时，非规约数的最高位d₀ = 0，因此，在该情形下，当d₀ ≠ 0时，该数必是规约数，但当d₀ = 0时，未必一定是非规约数，因为，当尾数不足p位时，若向左补0来编码，此时无论是规约数还是非规约数，d₀ 一定等于 0，所以，能使d₀ = 0的规约数有很多。

---

作者：黄邦勇帅(原名：黄勇）

2021-11-29

---