（五十）时间序列分析一：效应分解法

时间序列的效应分解

将时间序列分为趋势、周期、随机三个部分，并对前两个部分（稳定的可用于预测的）使用曲线拟合。

• 长期趋势变动：序列朝着一定的方向持续上升或下降，或停留在某一水平上的倾向。比如随着企业近段时间拓展业务，销售额稳步上升的趋势。
• 周期性/季节性变动：周期性通常是指经济周期，由非季节因素引起的与波形相似的涨落起伏波动，比如GDP增长率随经济周期的变化而变化。但是周期性变动稳定性不强，在实际操作中主要考虑的是季节性变动，比如啤酒的销售量在春夏季较高而在秋冬季较低、交通流量在上班高峰时大而其他时间小等。
• 随机变动：随机变动指随机因素导致时间序列的小幅度波动。

这三种效应可以组合成加法模型和乘法模型，即三种效应之间相加或者相乘，图形上的区别就是加法效应下季节效应的振幅随时间变化不大（第一行图），乘法效应下振幅逐渐增大（第二行图）。

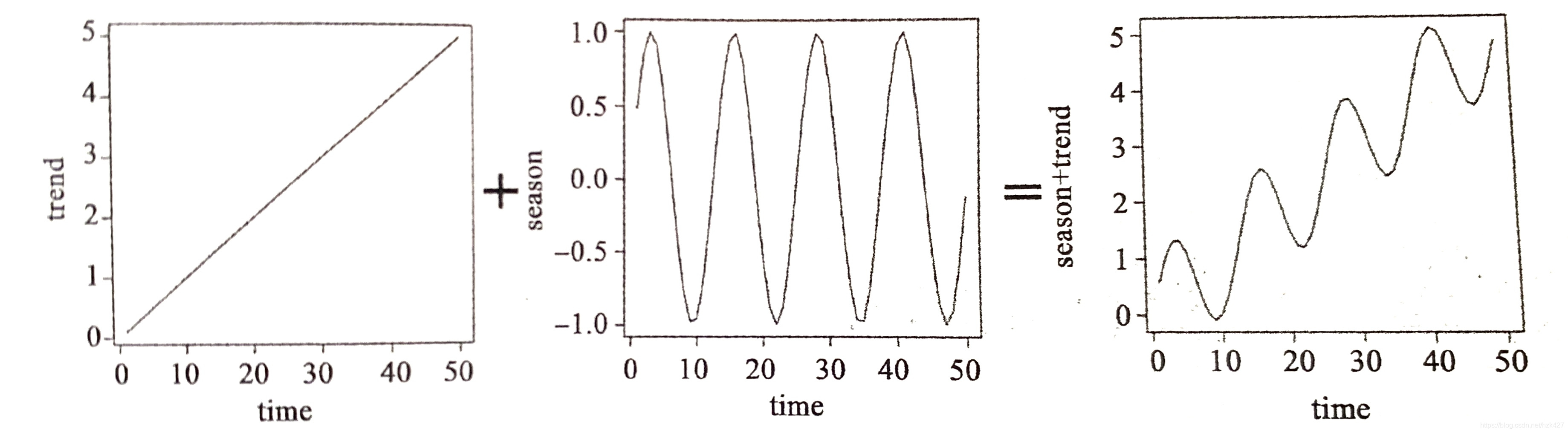
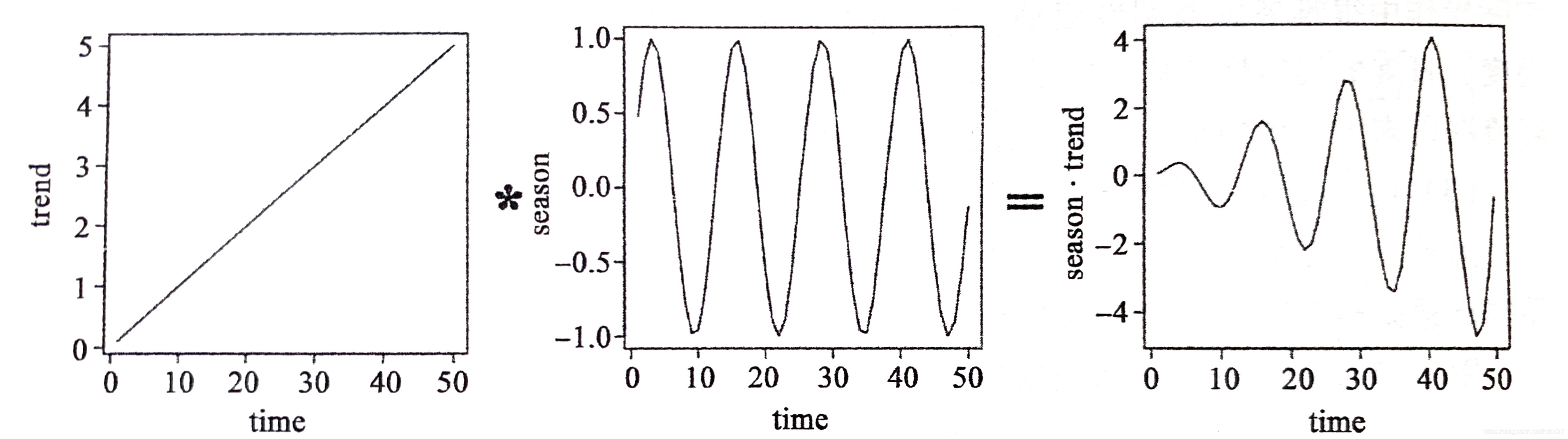
案例

AirPassengers数据集是一份某航空公司从1949年到1960年每月的客运量数据。可以使用Facebook数据科学家贡献的fbprophet包（安装时cmd里面运行 conda install -c conda-forge fbprophet）：

import pandas as pd
from fbprophet import Prophet
import matplotlib.pyplot as plt
df = pd.read_csv(r'C:\Users\lenovo\Desktop\AirPassengers.csv')
#将字符串改为日期
df['DATE'] = pd.to_datetime(df['DATE'])
df.head()
Out[4]: 
        DATE  AIR
0 1949-01-01  112
1 1949-02-01  118
2 1949-03-01  132
3 1949-04-01  129
4 1949-05-01  121

由于Prophet函数要求其只能处理单变量的时间序列，导入的数据第一列必须是日期类型的变量，变量名为“ds" ；第二列必须为数值类型的变量，变量名称必须为”y”：

df = df.rename(columns={'DATE':'ds','AIR':'y'})
df.head(2)
Out[6]: 
          ds    y
0 1949-01-01  112
1 1949-02-01  118
#看看该时间序列数据的趋势和周期性
pd.plotting.register_matplotlib_converters()
#上一条代码是因pandas版本的问题造成时间戳'Timestamp'的报错处理
ax = df.set_index('ds').plot(figsize=(12, 8))
ax.set_ylabel('Monthly Number of Airline Passengers')
ax.set_xlabel('Date')
plt.show()

下面使用Prophet函教对时间序列进行建模。虽然该函数有很多参数，但是大郎分采用默认即可。其中只有两个参数需要修改：growth参数用于指定长期趋势部分的拟合函数的形式，选项有Iiner和logistic两个。通过观察该数据集的趋势可以确定是线性趋势，假设发现时间序列的趋势是非线性的，无论是指数形式还是对数形式，均可以选择logstic；预测值的置信区间默认为80%，而我们常用的是95%，因此需要设置一下：

# 设置趋势的形式和预测值的置信区间为95% 
my_model = Prophet(growth='linear',interval_width=0.95)
my_model.fit(df)

接下来进行预测。make_future_dataframe函数用于准备好预测使用的日期字段，periods参数指定预测的期数，由于freq设置为“MS”代表月度数据，因此36期代表生成了3年的月度字段。predict函数使用只有日期字段的空表进行预测，其预测的输出变量较多，主要变量是时间序列的预测均值"yhat"，预测均值95%置信区间的下限"yhat_lower"，预测均值95%置信区间的上限"yhat_upper"：

future_dates = my_model.make_future_dataframe(periods=36, freq='MS')
forecast = my_model.predict(future_dates)
forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail(2)
Out[7]: 
            ds        yhat  yhat_lower  yhat_upper
178 1963-11-01  534.021253  488.073721  578.596021
179 1963-12-01  563.611828  517.280040  606.959414

最后展示预测的结果，其中uncertainty参数用于设置是否在图中展示置信区间：

my_model.plot(forecast,uncertainty=True)

在图中，蓝色的实线为预测的均值，浅蓝色区域为95%的置信区间，黑色的点为原始数据，最后三年为预测数据。可以发现随着时间的增长，季节效应的振幅逐渐增大，但是Prophet本身没有设置加法效应和乘法效应的选项，只能做加法效应模型。如果需要做乘法模型，只需要对时间序列取自然对数：

import numpy as np
df['y'] = np.log(df['y'])
my_model = Prophet(growth='linear',interval_width=0.95)
my_model.fit(df)
future_dates = my_model.make_future_dataframe(periods=36, freq='MS')
forecast = my_model.predict(future_dates)
my_model.plot(forecast,uncertainty=True)

可以看到，这个模型拟合效果更好（对比1957年-1961年那一段），预测更符合实际情况。也就是说如果季节效应随着趋势增加，就需要对数据取对数再建模。