01.神经网络和深度学习 —— week2 神经网络基础

2.1 二分类问题

1. 两个问题

• 实现神经网络如果遍历训练集，不需要用for循环；
• 为什么神经网络的计算过程可以分为前向传播和后向传播；

2. 给出几个符号及含义

• 样本$(x,y)$，训练样本包括m个；
• $x\in R^{n_x}$，表示样本x包含$n_x$个特征（hight * width * channel）；
• $y\in (0,1)$，目标值属于0,1分类；
• 训练数据：$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})$；
• $X=[x^{(1)},x^{(2)},...,x^{(m)}]，X.shape=(n_x,m)$；
• $Y=[y^{(1)},y^{(2)},...,y^{(m)}]，Y.shape=(1,m)$；

2.2 Logistic Regression

• $logisticregression$用于二分类问题的监督学习；
• 分类任务中：$Given$ $x$, $want$ $\hat{y}=P(y=1|x)$，其中$x\in R^{n_x}$， y ∈ { 0 , 1 } y \in \{0, 1\} y∈{0,1}， $\hat{y}\in [0,1]$；
• Parameters：$w\in R^{n_x}$，$b\in R$；
• 计算 $\hat{y}=w^{T}x+b$，引入sigmoid函数限制 $\hat{y}$ 取值范围：$\hat{y}=sigmoid(w^{T}x+b)=\sigma (w^{T}x+b)$；
• $\sigma (z)=\frac{1}{1+e^{-z}}$ ，${\sigma }^{\prime }(z)=\sigma (z)(1-\sigma (z))$；
• $sigmoid$函数图像：
  
  - 梯度消失问题；

2.3 Logistic Regression cost function

为了训练$logistic$回归模型的参数$w$以及$b$，需要定义一个成本函数。

1. recap

• ${\hat{y}}^{(i)}=\sigma (w^T{x}^{(i)}+b)$ $where$ $\sigma (z^{(i)})=\frac{1}{1+e^{-z^{(i)}}}$，$z^{(i)}=w^T{x}^{(i)}+b$
• $Given$ X = { x ( 1 ) , x ( 2 ) , . . . , x ( m ) } X = \{x^{(1)}, x^{(2)} , ... , x^{(m)} \} X={x(1),x(2),...,x(m)}，$want$ ${\hat{y}}^{(i)}\approx y^{(i)}$

2. loss (error) function

• 一般使用平方误差函数 $(squared$ $error）$：$L(\hat{y},y)=\frac{1}{2}(\hat{y}-y{)}^2$，但在logistic regression里，一般不用平方误差作为loss function，因为平方误差损失函数一般是非凸函数，使用梯度下降时，容易得到局部最优解，而不是全局最优。
• $logisticregression的lossfunction$： $L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$
  当 $y=1$ 时，$L(\hat{y},y)=-log\hat{y}$ ：$\hat{y}\to 1$时，$L(\hat{y},y)\approx 0$，表示预测效果越好；$\hat{y}\to 0$时，$L(\hat{y},y)\approx \infty$，表示预测效果越差；
  当 $y=0$ 时，$L(\hat{y},y)=-log(1-\hat{y}))$ ：$\hat{y}\to 0$时，$L(\hat{y},y)\approx 0$，表示预测效果越好；$\hat{y}\to 1$时，$L(\hat{y},y)\approx \infty$，表示预测效果越差；
• $lossfunction$是在单个训练样本中定义的，衡量了算法在单个训练样本上的表现。

3. Cost Function

• 衡量参数$w$和$b$在全体训练样本上的表现，是所有训练样本的$lossfunction$之和。
• $J(w,b)=\frac{1}{m}{\sum }_{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=-\frac{1}{m}{\sum }_{i=1}^m[(ylog\hat{y}+(1-y)log(1-\hat{y}))]$
• $CostFunction$是关于参数$w，b$的函数，我们的目标是迭代计算出最佳的$w和b$的值，最小化$CostFunction$，使其尽可能趋近于0。

2.4 梯度下降法

使用梯度下降法来训练或学习得到训练集上的参数$w$和$b$，使$cost$ $function$最小。

• r e p e a t : { repeat:\{ repeat:{
                        $w=:w-\alpha \frac{\delta J(w,b)}{\delta w}$
                         $b=:b-\alpha \frac{\delta J(w,b)}{\delta b}$
                  $\}$
  在程序代码中通常使用$dw$来表示$\frac{\delta J(w,b)}{\delta w}$，$db$来表示$\frac{\delta J(w,b)}{\delta b}$。
• 直观看梯度下降：
  
• 从低维解释梯度下降：
  

2.5 计算图

一个神经网络的计算都是按照前向或反向传播的过程来计算的。首先计算出神经网络的输出，接着进行反向传输操作（计算对应的梯度或导数）。

• 示例：
  

2.6 Logistc Regression中的梯度下降

• $Logistic$ $Regression$中的$loss$ $function$表达式：
  $z=w^{T}x+b$
  $\hat{y}=a=\sigma (z)$
  $L(a,y)=-(y\ast log(a)+(1-y)\ast log(1-a))$

• 反向传播过程：
  

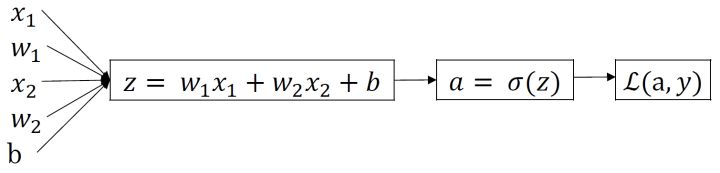
• 反向传播计算导数：

  $da=\frac{\delta L}{\delta a}=-\frac{y}{a}+\frac{1-y}{1-a}$

  $dz=\frac{\delta L}{\delta z}=\frac{\delta L}{\delta a}\cdot \frac{\delta a}{\delta z}=(-\frac{y}{a}+\frac{1-y}{1-a})\cdot a(1-a)=a-y$

  $d{w}_1=\frac{\delta L}{\delta w_1}=\frac{\delta L}{\delta z}\cdot \frac{\delta z}{\delta w_1}=(a-y)\cdot x_1$

  $d_b=\frac{\delta L}{\delta b}=\frac{\delta L}{\delta z}\cdot \frac{\delta z}{\delta b}=a-y$

• 参数更新：

  $w_1=:w_1-\alpha d{w}_1$
  $w_2=:w_2-\alpha d{w}_2$
  $b=:b-\alpha db$

2.7 m个样本的梯度下降

• $logistic$ $regression$ 中 $cost$ $function$表达：

  $z^{(i)}=w^T{x}^{(i)}+b$

  ${\hat{y}}^{(i)}=a^{(i)}=\sigma (z^{(i)})$

  $J(w,b)=\frac{1}{m}{\sum }_{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=-\frac{1}{m}{\sum }_{i=1}^m[(ylog\hat{y}+(1-y)log(1-\hat{y}))]$

• 全局成本函数实际上是 $1$ 到 $m$项损失函数和的平均，因此全局成本函数对$w_1$的导数，同样是各项损失函数对$w_1$导数和的平均值。即：

         $d{z}^{(i)}=a^{(i)}-y^{(i)}$

         $d{w}_1=\frac{1}{m}{\sum }_{i=1}^{m}d{z}^{(i)}\cdot x_1^{(i)}$

         $d{w}_2=\frac{1}{m}{\sum }_{i=1}^{m}d{z}^{(i)}\cdot x_2^{(i)}$

         $d_b=\frac{1}{m}{\sum }_{i=1}^m(a^{(i)}-y^{(i)})$

• 参数更新

2.8 向量化

深度学习的算法中，我们通常面临大数据集，程序编写过程中，尽可能减少loop循环语句，使用向量化提高程序运行速度。

• 逻辑回归向量化
  输入矩阵$X:(n_x,m)$
  权重矩阵$w:(n_x,1)$
  偏置变量$b:一个常数$
  输出矩阵$Y:(1,m)$

• 单次迭代梯度下降算法流程：

#正向
Z = np.dot(w.T,X)+b
A = sigmoid(Z)
#反向
dZ = A - Y
dw = 1/m * np.dot(X,dZ.T)
db = 1/m * np.sum(dZ)
#参数更新
w = w - alpha * dw
b = b - alpha * db

2.9 logistic regression cost function 的解释

预测输出$\hat{y}=\sigma (w^{T}x+b)，where$ $\sigma (z)=\frac{1}{1+e^{-z}}$，$\hat{y}$表示预测输出为正类（+1）的概率。

• $loss$ $function:$
  $\hat{y}=P(y=1|x)$：当$y=1$时，$P(y|x)=\hat{y}$；当$y=0$时，$P(y|x)=1-\hat{y}$。
  上述两种情况整合到一起，即$P(y|x)={\hat{y}}^y(1-\hat{y}{)}^{1-y}$。
  对上式进行log处理（单调函数不影响原函数的单调性）：
  $logP(y|x)=log({\hat{y}}^y(1-\hat{y}{)}^{1-y})=ylog\hat{y}+(1-y)(1-\hat{y})$
  概率$P(y|x)$表示预测的准确性，越大越好。对上式加上负号，转化为单个样本的$loss$函数，期望越小越好：
  $L(\hat{y},y)=-(ylog\hat{y}+(1-y)(1-\hat{y}))$
• $cost$ $function:$
  $m$个训练样本时，假设样本之间独立同分布，则：

       $P(label$ $in$ $labelset)={\prod }_{i=1}^{m}P(y^{(i)}|x^{(i)})$

  $\Rightarrow logP(...)={\sum }_{i=1}^{m}P(y^{(i)}|x^{(i)})=-{\sum }_{i=1}^{m}L(\hat{y},y)$

        此时$cost$ $function:$（因为$cost$求最小，加负号）

       $J(w,b)=\frac{1}{m}{\sum }_{i=1}^{m}L(\hat{y},y)=-\frac{1}{m}{\sum }_{i=1}^m(ylog\hat{y}+(1-y)(1-\hat{y}))$

参考资料：

[1] Andrew Ng 课程笔记连载：https://zhuanlan.zhihu.com/p/29688927
[2] 网易云课堂 Andrew Ng课程

本周编程作业链接：https://blog.csdn.net/iCode_girl/article/details/86702982
测验链接：https://blog.csdn.net/u013733326/article/details/79865858