HMM模型

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。隐马尔可夫模型（HMM）可以用五个元素来描述，包括2个状态集合和3个概率矩阵：1. 隐含状态 S、2. 可观测状态 O、3. 初始状态概率矩阵 π、4. 隐含状态转移概率矩阵 A、5. 观测状态转移概率矩阵 B 。

马尔科夫链

对于一个马尔可夫链来说，第n+1刻的状态只跟第n刻的状态有关，与第n-1,n-2,n-3,…等时刻的状态是没有任何关系的。

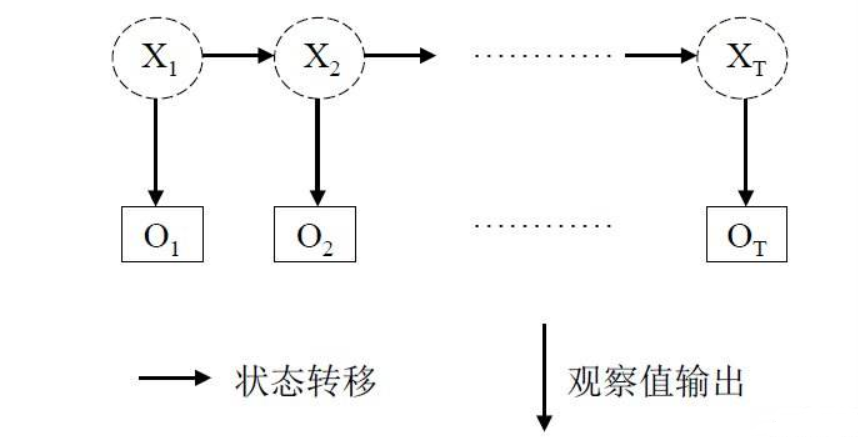
隐马尔科夫模型

对于上图，有两个行数据，这两列数据分布的特点，第一行是x行，第二行是o行，x行的某一个状态依赖于前一个状态,x行的每一个都指向o行其中的一个.

对于上图，一般把x行称为状态序列，o行称为观测序列，状态序列和观测序列是什么？
状态序列：隐藏的马尔科夫链随机生成的状态序列，称为状态序列。
观测序列：每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列
所以有马尔科夫模型定义：隐马尔可夫模型是一个关于时序的概率模型，它描述了一个由隐藏的马尔可夫链生成状态序列，再由状态序列生成观测序列的过程。其中，状态之间的转换以及观测序列和状态序列之间都存在一定的概率关系。

HMM 表示

设Q是所有可能的状态的集合，V是所有可能的观测的集合。

Q=q1,q2,…,qN,V=v1,v2,…,vM
其中，N是可能的状态数，M是可能的观测数。

I是长度为T的状态序列，O是对应的观测序列。

I=(i1,i2,…,iT),O=(o1,o2,…,oT)
A是状态转移矩阵：A=[aij]N×N
i=1,2,…,N;j=1,2,…,N
其中，在时刻t，处于qi 状态的条件下在时刻t+1转移到状态qj 的概率：

aij=P(it+1=qj|it=qi)
B是观测概率矩阵：B=[bj(k)]N×M
k=1,2,…,M;j=1,2,…,N
其中，在时刻t处于状态qj 的条件下生成观测vk 的概率：

bj(k)=P(ot=vk|it=qj)
π是初始状态概率向量：π=(πi)
其中，πi=P(i1=qi)
隐马尔科夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定。π和A决定状态序列，B决定观测序列。因此，隐马尔科夫模型λ可以由三元符号表示，即：λ=(A,B,π)。A,B,π称为隐马尔科夫模型的三要素。

两个假设

（1）：设隐马尔科夫链在任意时刻t的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻t无关。（齐次马尔科夫性假设）

（2）：假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他观测和状态无关。（观测独立性假设）

示例

wiki上面有一个预测病人是否感冒的例子
想象一个乡村诊所，村名的身体状况要么健康要么发烧，他们只有问诊所的医生的才能知道是否发烧。医生通过询问村名的感觉去诊断他们是否发烧。村民自身的感觉有正常、头晕或冷。
假设一个病人每天来到诊所并告诉医生他的感觉。假设病人的健康状况是一个离散马尔可夫链。病人的状态有两种：健康和发烧，但医生不能直接观察到，这意味着状态对医生是不可见的。
每天病人会告诉医生自己有以下几种由他的健康状态决定的感觉的一种：正常、冷或头晕。这些是观察结果。 整个系统为一个隐马尔可夫模型(HMM)。
现状：医生知道村民的总体健康状况，还知道发烧和没发烧的病人通常会表明自己有什么症状。 换句话说，医生知道隐马尔可夫模型的参数。
根据收集到的信息，得出以下的数据。
病人的状态，也就是Q(‘Healthy’, ‘Fever’)
病人的感觉，即观测状态，也就是V：(‘normal’, ‘cold’, ‘dizzy’)
π是初始状态概率向量:{‘Healthy’: 0.6, ‘Fever’: 0.4}
状态转移矩阵：

transition_probability = {
   
   'Healthy' : {
   'Healthy': 0.7, 'Fever': 0.3},
   'Fever' : {
   'Healthy': 0.4, 'Fever': 0.6},
   }

观测概率矩阵：

emission_probability = {