经典皇后问题

 

题目描述:编写一个程序求解皇后问题：在n×n的方格棋盘上，放置n个皇后，要求每个皇后不同行、不同列、不同左右对角线。

 

解法一：递归算法

 

设f(i,n)表示在n×n的方格棋盘上，已放置好第1个，...，第i-1个皇后，现要放置第i个，...，第n个皇后。放置前i个皇后的解法f(i,n)和放置前i+1个皇后的解法f(i+1,n)是相似的。求解皇后问题的递归模型如下。

①f(i,n):若i=n，则n个皇后放置完毕，输出解。

②f(k,n):在第k列上找到合适的位置放置一个皇后，f(k+1,n)。

 

接下来问题的关键是如果找到这个合适的位置，使得每个皇后不同行、不同列、不同左右对角线。

①显然不同列是成立的。因为前面k-1个皇后分别放置在1~k-1列，而该皇后则放在k列上。

②假设前面第j(1<=j<=k-1)个皇后，放置在位置为(q[j],j)的方格上，其中q[j]为行，j为列。则要求与(i,k)位置的皇后不同行的条件为：q[j]!=i;

③先来看一下图1：

 

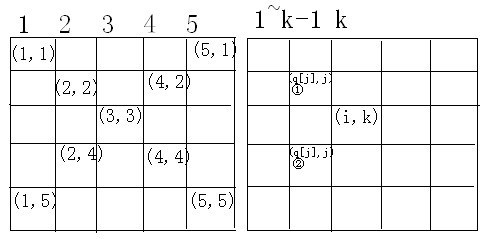
我们会发现一个简单的规律：即同一条对角线上的由左上方到右下方的每个元素有相同的“行-列”值，1-1=2-2=...=5-5。同样，在同一条对角线上的由右上方到左下方的每个元素则有相同的“行+列”的值，1+5=2+4=...=5+1。然后，根据右图可得到一下结论：当q[j]-j==i-k或则q[j]+j==i+k时，它们才在同一对角线上。两式一项整理得：当且仅当|q[j]-1|==|j-k|时，两个皇后在同一条对角线上。

 

对应的递归算法如下：
void Queens(int k,int n)
{
            if(k==n) 输出第一个解；
            else
                   for(int i=1;i<=n;i++)
                        if(第k列的第i行合适)
                        {
                          在位置处放一个皇后即q[k]=i;
                          Queens(k+1,n);
                         }
}

 

C++实现如下：

 

#include<iostream> #include<cstdlib> using namespace std; const int N=20; //最多皇后个数 int q[N]; //存放皇后所在的行号 int count=0; //存放解的个数 void Print(int n) //输出一个解 { count++; int i; cout<< "第" << count << "个解:"; for(i=1;i<=n;i++) cout<< "(" << i << "," << q[i] << ")"; cout<<endl; } int Place(int i,int k)//测试第k列的i行上能否摆放皇后 { int j; j=1; while(j<k) //j=1~k-1是已放置了皇后的列 { if((q[j]==i) || (abs(q[j]-i)==abs(j-k))) //第j列皇后是否在i行上，位置(q[j],j)与(i,k)是否同对角线 return 0; j++; } return 1; } void Queens(int k,int n)//第k个皇后放到第k列上 { if(k>n) Print(n); //所有皇后放置结束 else for(int i=1;i<=n;i++)//在第k列上穷举每一个位置 if(Place(i,k)) { q[k]=i; Queens(k+1,n); } } void main() { int n; //n存放实际皇后个数 cout<< "皇后问题(n<20) n:"; cin>> n; if(n>20) cout<< "n值太大，不能求解/n"; else { cout<< "皇后问题求解如下:"<<endl; Queens(1,n); cout<<endl; } }

 

皇后问题(n<20) n:6
皇后问题求解如下:
第1个解:(1,2)(2,4)(3,6)(4,1)(5,3)(6,5)
第2个解:(1,3)(2,6)(3,2)(4,5)(5,1)(6,4)
第3个解:(1,4)(2,1)(3,5)(4,2)(5,6)(6,3)
第4个解:(1,5)(2,3)(3,1)(4,6)(5,4)(6,2)

请按任意键继续. . .