读书笔记《机器学习》： 第八章：集成学习

目录：
8.1 个体与集成
8.2 Boosting
8.3 Bagging与随机森林
8.4 结合策略
8.5 多样性

---

8.1 个体与集成

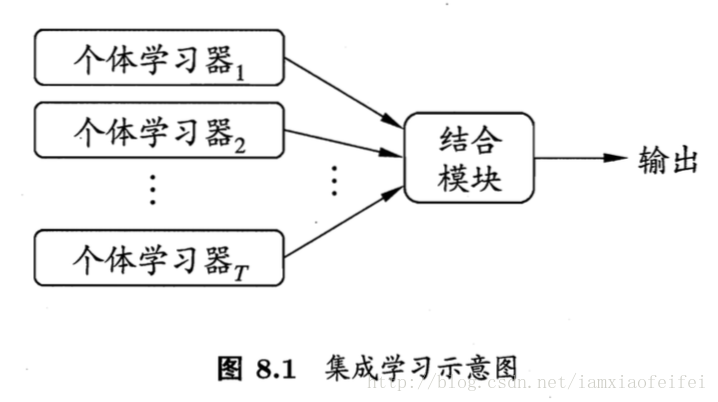
集成学习（ensemble learning）通过构建并结合多个学习器来完成学习任务。
同质集成：同质集成中的个体学习器也叫基学习器（base learner）
异质集成：异质集成中的个体学习器一般称组件学习器（component learner）

弱学习器（weak learner）指泛化性能略优于随机猜测的学习器。

假设基分类器的错误率相互独立，由hoeffding不等式可以推出集成的错误率，随着集成的个体分类器的数目的增加，集成的错误率将呈指数级下降，最终趋向于0.

集成学习研究的核心就是产生并结合“好而不同”的个体学习器。

集成学习主要分为两类：
1. 个体学习器存在强依赖关系，必须串行生成的序列化方法，代表adboost
2. 个体学习器不存在强依赖关系，可同时生成的并行化方法，代表bagging和随机森林。

8.2 Boosting

Boosting的工作机制：
先从初始训练集训练一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器。重复进行，直至基学习器数目达到指定的值，最终将这些基学习器加权结合。

基于加性模型迭代式优化指数损失函数角度推倒Adboost。
待补充

注意：
Boosting算法要求基学习器能对特定的数据分布进行学习。对于可以接受带权样本的基学习算法，可以通过重赋权法（re-weighting），在训练的每一轮中根据样本分布对训练样本重新赋予权重。对无法接受待权样本的基学习算法，可以使用重采样法（re-sampling）。

偏差-方差分解：Boosting使用的是弱分类器，主要关注降低偏差，能基于泛化性能弱的基学习器构造出很强的集成。

---

8.3 Bagging与随机森林

Bagging：对包含m个样本的训练集，使用自助采样法（bootstrap sampling）进行m次随机采样，生成T个包含m个样本的采样集，然后针对每个采样集生成一个学习器，再将这些学习器结合（分类任务简单投票即可，回归任务简单平均即可）即可。

训练一个bagging学习器与直接使用基学习算法训练一个学习器的复杂度同阶。
bagging算法可以不加修改的应用于多分类、回归任务。

由于使用了自助采样，对于每个基学习器而言，只使用了初始训练集中大约63.2%的样本，剩下约36.8%的样本可以当做验证集对泛化性能进行包外估计（out of bag estimate , 决策树的话还可以用于剪枝）

bagging主要关注降低方差，所以需要使用一些比较强的学习器，不如不剪枝的决策树、神经网络等。

随机森林：
两大扰动：样本扰动、属性扰动（一般log2d）
样本扰动就是初始训练集采样bootstrap sampling
属性扰动就是初始属性集采样
使得个体学习器的差异增加，从而使得最终集成的泛化性能增加。

一般地，随机森林的训练效率一般优于bagging，因为随机森林多了一个属性扰动，训练选择最优属性的时候只考察了属性子集而非全集。

8.4 结合策略

学习器结合的三个好处：

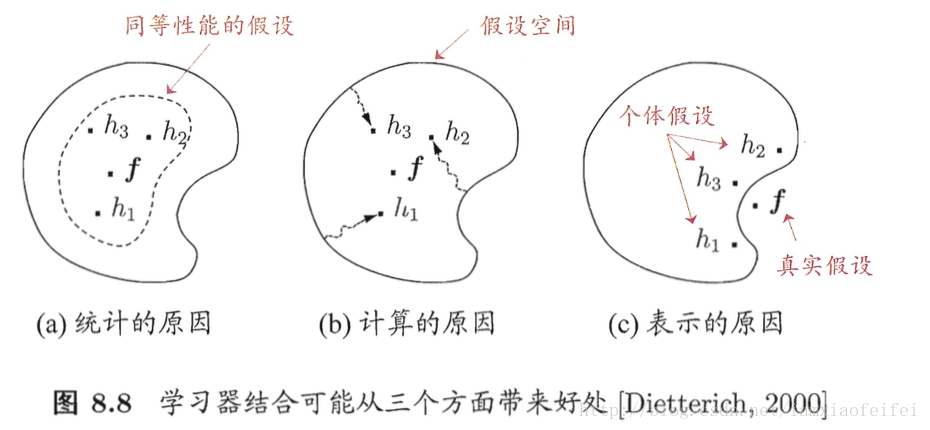
这个图非常的形象
1. 统计角度：学习任务的假设空间往往很大，可能有多个假设在训练集上达到同等性能，单单使用一个可能泛化性能不佳，但是结合多个可以降低这一风险。
2. 计算角度：算法有可能陷入局部极小值，结合多个可以降低这一风险
3. 表示角度：真实可能可能和我学习器的假设根本不在一个空间，结合多个可以使得假设空间变大，更有可能接近真实假设。

结合策略：
1. 数值型输出常常使用平均法
简单平均法
加权平均法
一般在个体学习器性能差异较大时使用加权平均，差异较小时使用简单平均法。
2. 分类任务常使用投票法
绝对多数投票法
相对多数投票法
加权投票法
还有软投票、硬投票一说，一个投0或1，一个输出概率值
如果基学习器类型不同，则其输出概率值不具有可比性，须将结果转换成硬投票0或1.

Stacking
Stacking是学习法的典型代表，相当于把各个基学习器的结果当做输入特征，其真实结果当做Label，训练一个次级学习器（也叫元学习器meta-learner）

一般使用交叉检验，避免直接使用训练初始学习器的训练集直接训练，这样吧很容易过拟合。使用初始学习器未使用的样本训练次级学习器。

8.5 多样性

误差-分歧分解（error-ambiguity decomposition）：个体学习器准确性越高、多样性越大，则集成越好。

通过这个误差-分歧分解，也可以很好地说明为什么集成学习追求的是好而不同的个体学习器。

多样性度量的指标：
不合度量（disagreement measure）
相关系数（correlation coefficient）
Q-统计量（Q-statistics）
$\kappa$-统计量

多样性增强的方法：
1. 数据样本扰动：bagging 自助采样，Adboost 序列采样
决策树、神经网络对数据敏感
线性学习器、支持向量机、朴素贝叶斯、KNN常被称为稳定基学习器（stable base learner），对这类数据样本扰动效果不明显

1. 输入属性扰动
2. 输出表示扰动
3. 算法参数扰动