[算法]平方根倒数速算法FISR详解，STM32G071实战测试

家介绍经典C语言平方根倒数速算法（或称Fast Inverse Square Root）。详细推导魔法数字0x5f3759df究竟从何而来，并最终在MCU上对比该算法和<math.h>中double sqrt(double)方法的性能表现并给出使用建议。本文不涉及高深的数学变换或复杂的计算机原理，但希望读者具备一些C语言基础；此外任何相关领域的积累都可能有助于内容理解。

希望本文能帮助到有需要的朋友。

平方根倒数简介

求平方根倒数在向量单位化操作中很常见，先举个例子，假设在二维平面内有一向量：

将该向量单位化，即将向量模长缩放为1，用向量除以它的模，可以表达成下式：

此处，单位向量的坐标，即是原向量坐标和模长倒数的乘积。

一般而言，对任一数x， 

 即被称作平方根倒数。

C语言内求平方根倒数

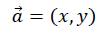
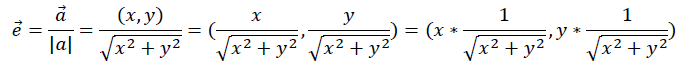
C语言内求平方根属于常规操作，因为<math.h>中已经提供了double sqrt(double)函数给大家调用，该函数接收一个double型变量，并返回其平方根。部分场合使用float类型，如果是我，我会这么写：

#include <math.h>

float x =0;

float inverse_square_root =0;

inverse_square_root =1/sqrt(x);

事实上，大多数计算机处理加法和乘法时更快，对于除法和开方运算，速度相对较慢。定义在<math.h>中的sqrt()方法其系统开销是比较大的，尤其在部分MCU上，有时不能很好地满足系统实时性要求。

速算法介绍

该情景与上世纪末PC算力较低的情况颇有几分相似，而在那段PC内存按MB计算的岁月里，优秀的C语言程序员们找到了该问题的解决方法：平方根倒数速算法（Fast Inverse Square Root），据说该算法最早由GaryTarolli在SGI Indigo开发中使用，对起源感兴趣的朋友可自行探究。

平方根倒数速算法是一个单独的函数实现，代码如下：

float FInvSqrtRoot(float x)

{

    long i = 0;

    float y, halfx;

    halfx = 0.5 * x;

    i = *(long*) &x;                 // 按照整型方法操作浮点数

    i = 0x5f3759df - (i >> 1);       // 魔法？

    y = *(float*) &i;                // 获得平方根倒数近似值

    y = y * (1.5 - halfx * y * y);   // 一次牛顿迭代

    return y;

}

该函数接收一个float型变量，并返回其平方根倒数。

Step1.奇怪的地址类型转换

i = *(long *) &x;                // 按照整型方法操作浮点数

代码第四行将浮点数x按照整型数据操作，这里的操作方法与类型转换有很大不同；类型转换将内存中按照浮点数标准表示的值近似为最接近的整数，并按照整数标准储存在内存中，像这样：i=(long)x;要理解*(long *) &x与(long)x的不同，需要了解浮点数在计算机中的表示方法。
浮点数在计算机中使用类似科学计数法的形式储存，float类型的浮点数使用32bit表示，结构如下：

最高位，第31位，为符号位，若S=0，该浮点数为正数；若S=1，该浮点数为负数。
接下来的8位数字，为指数部分，指数E范围为[0，255]，为可以表示负指数，规定在E的范围基础上-127，即[-127，128]；例如E=3表示2^(3-127)=2^(-124)。
接下来的23位数字，为尾数部分，即有效数字部分。由于二进制下有效数字必为1.xxx的形式，整数部分必为1，因此无需使用第22位表示整数1，而是直接表示小数点后一位，整数部分不在尾数M中体现，只在计算时加上；即M=0101…表示二进制的1.0101。以上，float型浮点数在内存中的存放形式已经明确。
现假设有一float型浮点正数x，其在内存中按照上述方式存放，即：

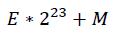
则x表示的浮点数值为：

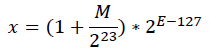
注意平方根倒数速算法只接收正数，所以全文只讨论x为正浮点数的情况。

此时再回来看i=*(long *) &x这行代码；

第一步；取x的地址，注意此时x的地址指向一个浮点数，内存中对应的数据为：E*2^23+M

第二步；将该地址转换为指向long整型的地址，注意转换的是地址类型而不是数据，现在内存中的数据仍然是：E*2^23+M

第三步，取该地址指向的数据，赋给i；此时程序将按照整型标准去读取这个数据。因此，可以将i理解为x对应内存数据的整型解释。现在可以对i进行整型支持的操作，比如接下来要用到的位移操作。

准备工作已经完成，现在进入算法的核心，即施放魔法：

i = 0x5f3759df - (i >> 1);       // 魔法？

要理解这行代码，需要一点点数学铺垫；我们先给x表示的浮点数取个对数：

其中，M表示尾数，M/2^23范围在[0,1)之间；在极限理论中，若x属于[0,1]，有以下关系：

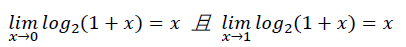
即在x接近0或1的条件下，log2(1+x)接近x；很明显当x不靠近0或1时，误差会变大，如下图左侧所示：

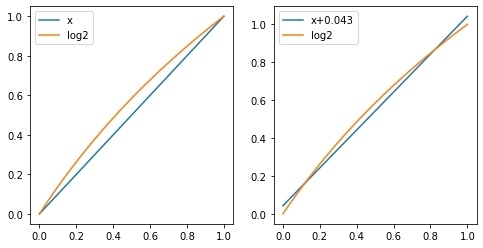
如果在等式右侧加入一个微小量u，可以使得x+u在[0,1]范围内近似log2(1+x)，如上图右侧所示：

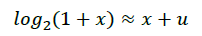
所以有：

因此，

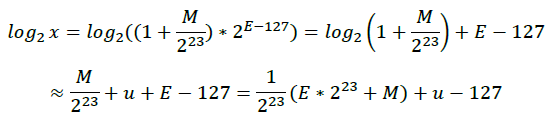
此时再倒回去看浮点数x在内存中的存放形式，即：E*2^23+M；

因此可以认为浮点数的对数形式与其内存存放形式相似，只是添加了缩放和平移。我们知道：

令：

所以有：

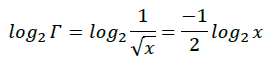
将上式展开：

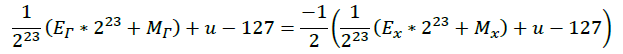
稍作整理： 

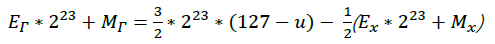
这太棒了，因为浮点数在内存中的存放形式，即：E*2^23+M

而上式中

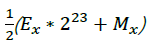
则相当于对其内存形式右移1位，即

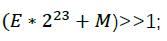
由此可知，魔法数字0x5f3759df就是包含u在内的修正项：

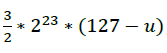
至此我们已经完成了魔法代码的解析：

 

这太棒了，因为浮点数在内存中的存放形式，即：E*2^23+M

而上式中

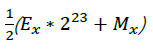
则相当于对其内存形式右移1位，即

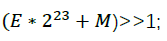
由此可知，魔法数字0x5f3759df就是包含u在内的修正项：

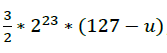
至此我们已经完成了魔法代码的解析：

i = 0x5f3759df - (i >> 1);       // 魔法

i就是x对应内存数据的整型解释，将i右移1位相当于乘以二分之一，也就是1/2*(Ex*2^23+Mx);

等式右侧的运算结果，就是 

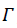
 ，也就是

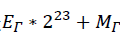
即

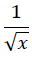
注意此时程序认为i是整型变量，所以需要下一行代码再将其转换为浮点型；

y = *(float *) &i;              // 获得平方根倒数估计值

此时y即是x的平方根倒数。

Step3.优化结果

由于上述推导中，引入了修正系数u，所以y只是近似解。

接下来使用牛顿法（Newton Method）进行一次迭代，使y更接近准确值。简单来说，使用牛顿法，可以从一个近似解获得一个更接近准确答案的解；牛顿法的核心思想是迭代，对于我们正在讨论的问题，属于已知x求y的类型，即

假设已经获取一个近似解y1，则可以通过一次迭代求取更优解y2：

神奇的是计算y2仅需要乘法和减法运算，于是有如下代码：

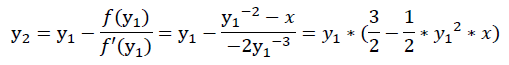
y = y * (1.5 - halfx * y * y);   // 一次牛顿迭代

该行代码返回优化后的平方根倒数，也就是最终运算结果。

性能测试
接下来我会在STM32G071上测试Fast Inverse Square Root算法与<math.h>中提供的double sqrt(double)算法的性能，并尝试以此证明它为何被尊为经典。STM32G071运行在64MHz下，编译器和调试器优化分别为-O0和-g3。
使用uint32_t替代long型：

float FInvSqrtRoot(float x)

{

    uint32_t i = 0;

    float y, halfx;

    halfx = 0.5 * x;

    i = *(uint32_t*) &x;             // 按照整型方法操作浮点数

    i = 0x5f3759df - (i >> 1);       // 施放魔法

    y = *(float*) &i;                // 获得平方根倒数近似值

    y = y * (1.5 - halfx * y * y);   // 一次牛顿迭代

    return y;

}

因为STM32G071的RAM大小为36KB，先构造了8000个float数据的数组，大小为32KB；构造方法如下：

float test_data[8000] ={ 0 };

for (uint16_t i = 0; i < 8000; i++)

  test_data[i] = i * 1000 + (float)i / 1000;

使用两种不同算法处理上述8000个数据，测试代码如下（注意此处仅作演示，测试方法不一定严谨）：

//平方根倒数速算法

printf("FISR Test Start!\r\n");

ticks = 0;//定时器计数，1ms/tick

HAL_TIM_Base_Start_IT(&htim1);

for (uint16_t i = 0; i < 8000; i++)

  sroot=FInvSqrtRoot(test_data[i]);

HAL_TIM_Base_Stop_IT(&htim1);

printf("FISR Test Stop!\r\n");

printf("FISR Time Elapsed:%f\r\n", ((float) ticks) / 1000);



//传统1/sqrt()

printf("SQRT Test Start!\r\n");

ticks = 0;

HAL_TIM_Base_Start_IT(&htim1);

for (uint16_t i = 0; i < 8000; i++)

  sroot=1 / sqrt(test_data[i]);

HAL_TIM_Base_Stop_IT(&htim1);

printf("SQRT Test Stop!\r\n");

printf("SQRT Time Elapsed:%f\r\n", ((float) ticks) / 1000);

在上述测试环境下，FInvSqrtRoot耗时181ms，1 / sqrt()耗时325ms，FInvSqrtRoot比1 / sqrt()快大约79%。由于sroot是float型，sqrt()返回double型，所以1 / sqrt()测试时有额外的类型转换损耗；将sroot更改为double型，则类型转换损耗由FInvSqrtRoot承担；该状态下，FInvSqrtRoot耗时187ms，1 / sqrt()耗时315ms，FInvSqrtRoot比1 / sqrt()快大约68%。注意FInvSqrtRoot求取的仅是平方根倒数的近似值，和1 / sqrt()比对，误差约在1%以内。
 

魔改：平方根速算法

根据上述原理，可将平方根倒数速算法修改为平方根速算法，代码如下：

float FSqrtRoot(float x) {

    uint32_t i = 0;

    float y;

    i = *(uint32_t *) &x;            // 按照整型方法操作浮点数

    i = 0x1fbd1df5 + (i >> 1);       // 施放魔法

    y = *(float *) &i;               // 获得平方根近似值

    y = 0.5 * (y + x / y);           // 一次牛顿迭代

    return y;

}

在上述测试环境下，FSqrtRoot耗时109ms，sqrt()耗时221ms，FInvSqrtRoot比sqrt()快大约100%。由于sroot是float型，sqrt()返回double型，所以sqrt()测试时有额外的类型转换损耗；将sroot更改为double型，则类型转换损耗由FSqrtRoot承担；该状态下，FSqrtRoot耗时115ms，sqrt()耗时208ms，FInvSqrtRoot比sqrt()快大约80%。

以上代码仅作原理演示用，已通过附件分享 

  FISR.zip  (474 Bytes)  ；
感兴趣的朋友可自行推导实验，算法性能也请根据实际需求比对。
---------------------
作者：Litthins
链接：https://bbs.21ic.com/icview-3160046-1-1.html
来源：21ic.com
此文章已获得原创/原创奖标签，著作权归21ic所有，任何人未经允许禁止转载。