合成器基础(一) - 声音基础知识

目录

声音基础知识

音调、泛音、谐波和分音

傅立叶转换和泛音

频谱

其他波形属性

---

声音基础知识

        从技术上来说，声音是物理能量( physical energy )（如拍手）到空气压力扰动的转换。空气压力中的这种改变通过空气以一连串振动( vibrations )，即声波( a coustic wave )的形式传播。声音振动也可以通过其他介质传播，如墙壁或地板。

        如果振动以周期形式传播，我们就说声音具有波形( waveform )。

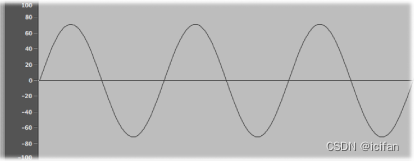
        上图显示了正弦波( sine )的示波图（图形显示），这是一种最简单的波形。 所有声音的波形，除了基本正弦波外，都由基频和多种其他不同的频率组成。

        如果振动不以可辨别的形式传播，则声音就称为噪音( noise )。

        波形的重复（示波器中的每个波峰和波谷）被称为循环。每秒钟发生的循环数决定波形的基本音高( basic pitch )，通常称为频率( frequency )。 

音调、泛音、谐波和分音

        声音的频率被称为基础音调。 （简称基音或基频，fundamental tone / frequency）。

        基频整数倍的非基础频率被称为泛音( overtones )与谐波( harmonics )。不是整数倍的非基础音调被称为分音( partials )。而若为基频的几分之几，则称为次泛音( subharmonic )。

        当发声体由于震动而发出声音时，声音一般可以分解为许多单纯的正弦波，也就是说所有的自然声音基本都是由许多频率不同的正弦波组成的，其中频率最低的正弦波即为基频，而其他频率较高的正弦波则为泛音。音乐演奏或歌唱中，基频是区别音高的主要元素，决定旋律( melody )。而泛音则决定乐器或人声的音色( timbre )。

        基础音调( fundamental tone )被称为第一谐波( 1st harmonic )，通常比其他泛音声音更大。

        以两倍于第一泛音频率弹奏的音调称为第一泛音( 1st overtone )或第二谐波( 2nd harmonic )。

        以三倍于第一泛音频率弹奏的音调称为第二泛音( 2nd overtone)或第三谐波( 3rd harmonic )。

以此类推，如下简化图表。

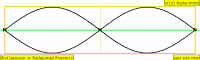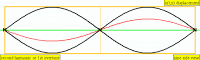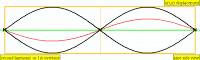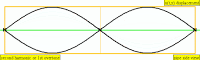
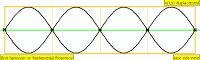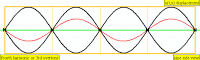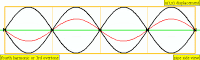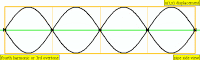
Frequency	Name 1	Name 2	Wave Representation
1 · f  = 440 Hz	fundamental tone	1st harmonic
2 · f  = 880 Hz	1st overtone	2nd harmonic
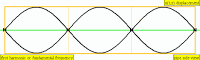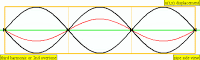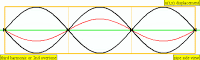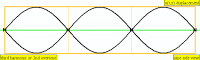
3 · f  = 1320 Hz	2nd overtone	3rd harmonic
4 · f  = 1760 Hz	3rd overtone	4th harmonic

        这些泛音中的每一个都拥有不同于基础音调的音色质量。大体来说，整数倍或能被整数（如八度音程、奇数或偶数泛音）除尽的泛音听起来都更具「音乐感」。相反的，不是整数倍或不能被整数除尽的音调称为不和谐谐波或分音音调。当将大量这类不和谐波音组合在一起时，听起来就会显得「嘈杂」。

傅立叶转换和泛音

        「任何周期性波( periodic wave )都可以看作某个波长( wavelength )和振幅( amplitude )的正弦波的叠加，这些正弦波的波长有着调和的关系（小数字的比率）」。这称为「傅立叶转换」( Fourier transform )。大体上用更接近音乐术语的话来说，这意味着任何带某个音高的音调都可以被当作一个正弦音调的混音。这包含了基本的基础音调及其泛音（谐波）。例如：在频率为440 Hz时，基本振荡（基础音调或第一谐波）为“A”。第二个泛音的频率加倍(880 Hz)，第三个则以3倍(1320 Hz)速度振荡，接下来的泛音以4倍速度类推，见前张附图。

频谱

将基础音调与不同电平( signal strength )的多种泛音结合起来时，听起来就会像声音。这些声音元素之间的电平关系会随时间改变。大量泛音的合并被称为泛音频谱，或者更常见的说法是频谱( f requency spectrum )。

频谱显示声音中的所有单个声音元素。从左到右，由低到高显示。所有泛音的相应电平以垂直方式表示，尖峰脉冲越高表示电平越高。

        插图显示在特定的时间点，基础音调和泛音之间的电平和频率关系。这些关系会随时间不断变化，造成频谱的不断变化，从而引起声音的变化。

其他波形属性

        正如先前所探讨过的，声波具有频率。声波的其他属性包括振幅、波长、周期和相位。

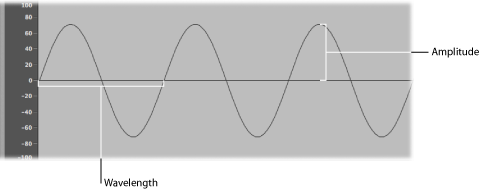
        振幅( amplitude )：波形的振幅表示空气压力改变的量。可以视为从零空气压力或「静止」（在插图中的0 dB处显示为水平线）开始的最大垂直距离。换一种说法，振幅是水平轴和波形峰值顶部（或波形波谷底部）的距离。 波长( wavelength )：波长是给定频率波形的重复循环间的距离。频率越高，波长越短。周期( period )：一个波完成一次整个波形循环旋转所花费的时间。频率越高越快，波的周期就越短。相位( phase )：相位与波形之间的时间形成对比，以0到360度计算。当两个波形在同一时间开始，就称它们相位符合( in phase )或相位对齐( phase alignment )。如果一个波形稍微迟于另一个波形，则称它们偏离相位( out of phase )。

       要辨别整个波周期的固定相位差异并不容易，但是如果其中一个波形的相位随时间改变，那就可以听出来。这在常见的音频效果，如镶边( flanging )和相位移动( phase-shifting )中会发生，见附图。

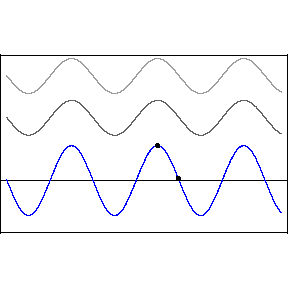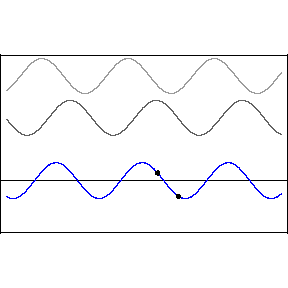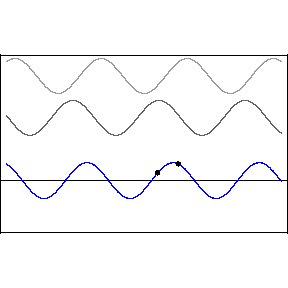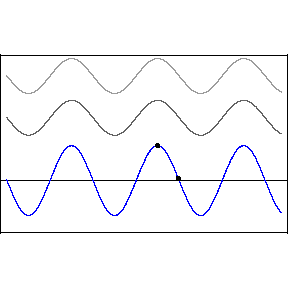
        当播放两个偏离相位的相同声音时，某些泛音或谐波会相互抵消，从而在这些区域中生成静音。这被称为相位抵消( phase cancellation )，发生在相同频率在同一电平处交叉的情况中。