树回归CART(Classification And Regression Tree)（2）

前面，我们分析了树回归的切分函数。但是如果一棵树节点过多，表明该模型可能对数据“过拟合”。为了避免过拟合，经常通过“剪枝”技术来降低决策树的复杂度。在前面chooseBestSplit()函数中设置的提前终止条件，实际上就是在进行一种所谓的的“预剪枝”。相对应的“后剪枝”则是需要训练集和测试集的共同作用。

1 预剪枝
我们在树回归中： 树的构建算法对输入的参数tolS 和 tolN 非常敏感。而去手动的修改参数并非一个明智的选择，而事实上，我们大多时间甚至不知道我们需要的结果是什么，因此“后剪枝”技术就应运而生，即利用测试集来对数进行剪枝，不需要我们指定参数，是一种跟接近于机器学习理念的剪枝方法。

2 后剪枝
后剪枝需要把数据集分为训练集和测试集，首先制定参数，使得构建出的原始树足够大，然后在该树上进行剪枝，从上到下找到叶节点，用测试集来验证是否可以将这些叶节点合并（利用测试误差来判断）。
伪代码：

基于已有的树切分测试数据：
    如果存在任一子集是一颗树，则在该子集递归剪枝过程
    计算将当前两个叶节点合并后的误差
    计算不合并的误差
    比较两个误差，如果误差降低，就降两个叶节点合并

#　后剪枝技术　prune.py

def isTree(obj):
    return(type(obj).__name__ == 'dict') # 测试输入变量是否是一棵树。返回布尔类型值

def getMean(tree):
    '从上到下遍历树，直到叶节点，如果找到两个叶节点就计算平均值（塌陷处理）'
    if isTree(tree['right']): #  右子树非叶节点
        tree['right'] = getMean(tree['right'])  # 递归
    if isTree(tree['left']):
        tree['left'] = getMean(tree['left'])   # 递归 直到找到叶节点
    return (tree['left']+tree['right'])/2.0 # 返回平均值

def prune(tree, testData): 
    '剪枝核心 参数：代建制的树 和剪枝所用的测试集'
    # 首先确认测试集是否为空，为空，即没有测试集，则对数进行塌陷处理。一旦非空，则对测试数据进行切分。
    if (np.shape(testaData)[0] == 0):
        return getMean(tree) # 进行塌陷处理（平均值）
    # 检查某个分支是子树还是叶节点，如果有是子树，则将调用prune函数对该子树进行剪枝
    if isTree(tree['right']) or isTree(tree['left']): 
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
    if isTree(tree['right']):
        tree['right'] = prune(tree['right'], rSet)
    if isTree(tree['left']):
        tree['left'] = prune(tree['left'], lSet)
    #　对左右两个分支完成剪枝后，还要检查它们是否还为子树。如果不再是子树，就可以合并
    if not isTree(tree['left']) and not isTree(tree['right']):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        errorNoMerge = sum(np.power(lSet[:, -1]-tree['left'], 2)) + sum(np.power(rSet[:, -1]-tree['right'], 2))  # 计算没有合并的误差
        treeMean  = (tree['left'] + tree['right'])/2.0
        errorMerge = sum(np.power(testData[:, -1]-treeMean, 2))
        if errorMerge < errorNoMerge:
            print("Merging")
            return treeMean
        else:
            return tree
    else: # 左右两个分支完成剪枝后，如果还是子树，返回tree
        return tree 

注
我们在刚开始对测试集检测是否为空，一旦非空，则对测试数据进行二元切分。切分的两个子集，被当作测试集来对相应的子树进行剪枝。

3 模型树
前面介绍的回归树的叶节点都是常数值，还有一种就是把叶节点设定为分段线性函数。

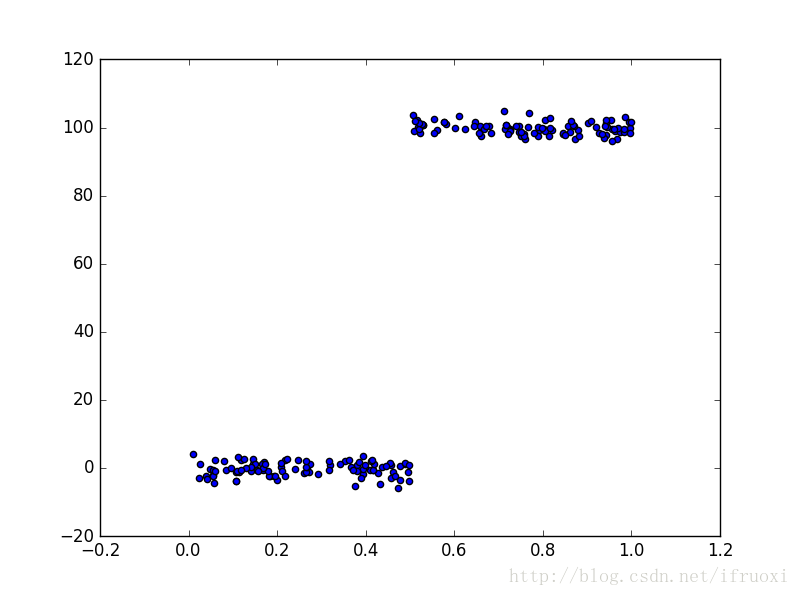
如图，显然分段线性模型可以更好的去建模。
我们在前面回归数的代码上进行修改来得到模型数的代码。
首先要利用树生成算法对数据进行切分，且每份切分数据都能很容易的被线性模型所表示。该算法的关键就是误差的计算。回顾前面的回归树，误差是：点与点之间的差值。在模型树中该误差计算方法不成立，因此可以先线性回归去拟合给定的数据集，然后计算真实目标值和预测值之间的误差，最后将这些误差值平方求和就得到最终的误差值

#　模型数的构建（误差计算）
def linearSolve(dataSet):
    '对所给数据进行线性回归拟合'
    m, n = np.shape(dataSet)
    X = np.mat(np.ones((m, n))) # 待拟合样本
    Y = np.mat(np.ones((m, 1))) # 预测值
    X[:, 1:n] = dataSet[:, 0:n-1] # 第一列全部为1 
    Y = dataSet[:, -1]
    XTX = X.T * X
    if np.linalg.det(XTX) == 0: # 行列式为0， 矩阵不可逆
        raise NameError('The Matrix cannot be inverse!')
    ws = XTX.I * (X.T * Y)
    return ws, X, Y
def modelLeaf(dataSet):  # 这个函数 与 树回归 的regLeaf函数功能一致
    ws, X, Y = linearSolve(dataSet)
    return ws
def modelError(dataSet):
    '计算误差'
    ws, X, Y = linearSolve(dataSet)
    yHat = X * ws
    return sum(np.power(Y - yHat, 2))

注
模型数的构建还是很简单的。创建模型树的时候需要将模型树函数作为creatTree(）的参数即可。
对于数据：

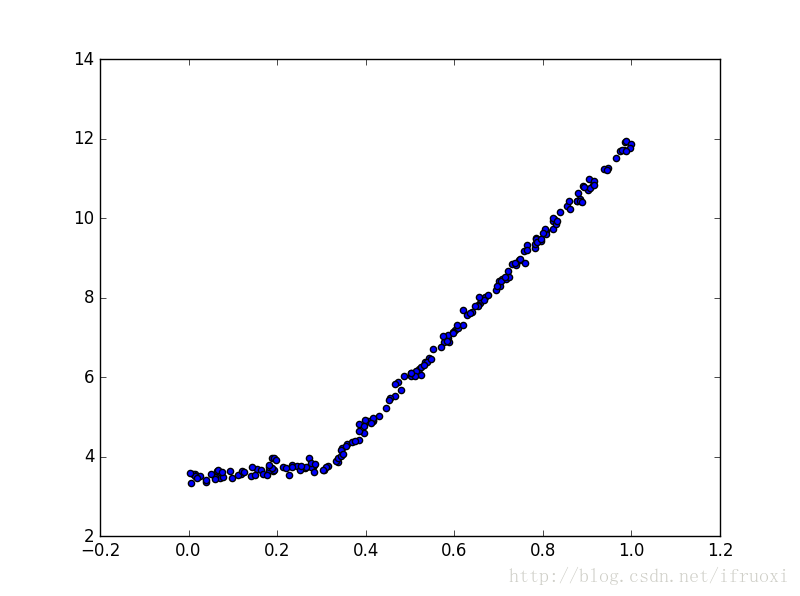
构建的模型树：

数据在0.28处分段生成两个线性模型：
$y = 3.468 + 1.185x$ 和 $y = 0.00169 + 11.965x$