Softmax Regression算法

<<上一篇 Logistic Regression算法

前言

Logistic Regression算法主要是用于处理二分类问题，若需要处理的是多分类问题，如手写字识别，即识别是{0,1,…,9}中的数字，此时，需要使用能够处理多分类问题的算法。
Softmax Regression算法是Logistic Regression算法在多分类问题上的推广，主要用于处理多分类问题，其中，任意两个类之间是线性可分的。

Softmax Regression模型

Softmax Regression算法适用于处理类标签$y$的取值大于等于2的线性可分的多分类问题。
假设$m$个训练样本 { ( X ( 1 ) , y ( 1 ) ) , ( X ( 2 ) , y ( 2 ) ) , . . . , ( X ( m ) , y ( m ) ) } \{({{X}^{(1)}},{{y}^{(1)}}),({{X}^{(2)}},{{y}^{(2)}}),...,({{X}^{(m)}},{{y}^{(m)}})\} {(X(1),y(1)),(X(2),y(2)),...,(X(m),y(m))} ，对于Softmax Regression算法，其输入特征为：$X^{(i)}\in R^{n+1}$，类标记为： y ( i ) ∈ { 0 , 1 , . . . , k } {{y}^{(i)}}\in \{0,1,...,k\} y(i)∈{0,1,...,k}。假设函数为每一个样本估计其所属的类别的概率$P(y=j|X)$，具体的假设函数为：

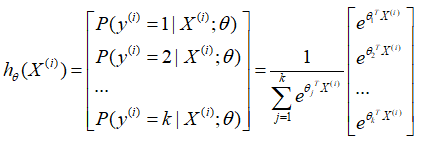
其中$\theta$表示的向量，且${\theta }_i\in R^{n+1}$。则对于每一个样本估计其所属的类别的概率为：
$$P(y^{(i)}=j|X^{(i)};\theta )=\frac{e^{{{\theta }_j}^T{X}^{(i)}}}{{\sum }_{l=1}^k{e}^{{{\theta }_l}^T{X}^{(i)}}}$$

Softmax Regression算法的代价函数

类似于Logistic Regression算法，在Softmax Regression算法的损失函数中引入指示函数$I(.)$，其具体形式为：

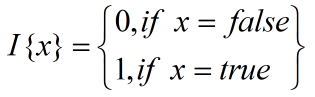
那么，对于Softmax Regression算法的损失函数为：
J ( θ ) = − 1 m [ ∑ i = 1 m ∑ j = 1 k I { y ( i ) = j } log ⁡ e θ j T X ( i ) ∑ l = 1 k e θ l T X ( i ) ] J(\theta )=-\frac{1}{m}\left[ \sum\limits_{i=1}^{m}{\sum\limits_{j=1}^{k}{I\{{{y}^{(i)}}=j\}\log \frac{{{e}^{{{\theta }_{j}}^{T}{{X}^{(i)}}}}}{\sum\limits_{l=1}^{k}{{{e}^{{{\theta }_{l}}^{T}{{X}^{(i)}}}}}}}} \right] J(θ)=−m1​⎣⎢⎢⎢⎡​i=1∑m​j=1∑k​I{y(i)=j}logl=1∑k​eθl​TX(i)eθj​TX(i)​⎦⎥⎥⎥⎤​
其中， I { y ( i ) = j } I\{y^{(i)}=j\} I{y(i)=j}表示的是当$y^{(i)}$属于第$j$类时， I { y ( i ) = j } = 1 I\{y^{(i)}=j\}=1 I{y(i)=j}=1，否则， I { y ( i ) = j } = 0 I\{y^{(i)}=j\}=0 I{y(i)=j}=0。

Softmax Regression算法的求解

对于上述的代价函数，可以使用梯度下降法对其进行求解，首先对其进行求梯度：
∇ θ j J ( θ ) = − 1 m ∑ i = 1 m [ ∇ θ j ∑ j = 1 k I { y ( i ) = j } log ⁡ e θ j T X ( i ) ∑ l = 1 k e θ l T X ( i ) ] {{\nabla }_{{{\theta }_{j}}}}J(\theta )=-\frac{1}{m}\sum\limits_{i=1}^{m}{\left[ {{\nabla }_{{{\theta }_{j}}}}\sum\limits_{j=1}^{k}{I\{{{y}^{(i)}}=j\}\log \frac{{{e}^{{{\theta }_{j}}^{T}{{X}^{(i)}}}}}{\sum\nolimits_{l=1}^{k}{{{e}^{{{\theta }_{l}}^{T}{{X}^{(i)}}}}}}} \right]} ∇θj​​J(θ)=−m1​i=1∑m​[∇θj​​j=1∑k​I{y(i)=j}log∑l=1k​eθl​TX(i)eθj​TX(i)​]
当$y^{(i)}=j$时，$${\nabla }_{{\theta }_j}J(\theta )=-\frac{1}{m}\sum _{i=1}^m\left[\frac{{\sum }_{l=1}^k{e}^{{{\theta }_l}^T{X}^{(i)}}-e^{{{\theta }_j}^T{X}^{(i)}}}{{\sum }_{l=1}^k{e}^{{{\theta }_l}^T{X}^{(i)}}}\cdot X^{(i)}\right]$$
当$y^{(i)}̸=j$时，$${\nabla }_{{\theta }_j}J(\theta )=-\frac{1}{m}\sum _{i=1}^m\left[\frac{-e^{{{\theta }_j}^T{X}^{(i)}}}{{\sum }_{l=1}^k{e}^{{{\theta }_l}^T{X}^{(i)}}}\cdot X^{(i)}\right]$$
最终的结果为：
− 1 m ∑ i = 1 m [ X ( i ) ⋅ ( I { y ( i ) = j } − P ( y ( i ) = j ∣ X ( i ) ; θ ) ) ] -\frac{1}{m}\sum\limits_{i=1}^{m}{\left[ {{X}^{(i)}}\cdot (I\{{{y}^{(i)}}=j\}-P({{y}^{(i)}}=j|{{X}^{(i)}};\theta )) \right]} −m1​i=1∑m​[X(i)⋅(I{y(i)=j}−P(y(i)=j∣X(i);θ))]
注意，此处的${\theta }_j$表示的是一个向量。通过梯度下降法的公式可以更新：
$${\theta }_j={\theta }_j-\alpha {\nabla }_{{\theta }_j}J(\theta )$$

Softmax Regression与Logistic Regression的关系

在Softmax Regression中存在着参数冗余的问题。简单来讲就是参数中有些参数是没有任何用的，为了证明这一点，假设从参数向量${\theta }_j$中减去向量$\psi$，假设函数为：
$$P(y^{(i)}=j|X^{(i)};\theta )=\frac{e^{{({\theta }_j-\psi )}^T{X}^{(i)}}}{{\sum }_{l=1}^k{e}^{{({\theta }_l-\psi )}^T{X}^{(i)}}}=\frac{e^{{{\theta }_j}^T{X}^{(i)}}\cdot e^{-{\psi }^T{X}^{(i)}}}{{\sum }_{l=1}^k{e}^{{{\theta }_l}^T{X}^{(i)}}\cdot e^{-{\psi }^T{X}^{(i)}}}=\frac{e^{{{\theta }_j}^T{X}^{(i)}}}{{\sum }_{l=1}^k{e}^{{{\theta }_l}^T{X}^{(i)}}}$$
从上面可以看出从参数向量${\theta }_j$中减去向量$\psi$对预测结果并没有任何影响，也就是说在模型中，存在着多组的最优解。
Logistic Regression算法是Softmax Regression的特征情况，即$k=2$时的情况，当$k=2$时，Softmax Regression算法的假设函数为：

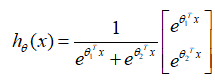
利用Softmax Regression参数冗余的特点，令$\psi ={\theta }_1$，从两个向量中都减去这个向量，得到：

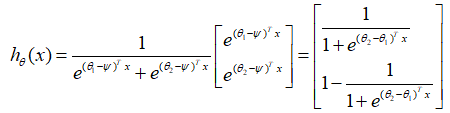
在Logistic Regression算法中，假设函数为：

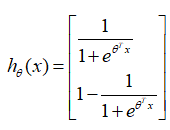
由上述的$k=2$时的Softmax Regression的假设函数和Logistic Regression的假设函数可知，两者是等价的。

Python代码实现

下述代码在Python2.7中通过。
训练数据SoftInput.txt为：

-0.017612	14.053064	2
-1.395634	4.662541	3
-0.752157	6.53862	3
-1.322371	7.152853	3
0.423363	11.054677	2
0.406704	7.067335	3
0.667394	12.741452	2
-2.46015	6.866805	3
0.569411	9.548755	0
-0.026632	10.427743	2
0.850433	6.920334	3
1.347183	13.1755	2
1.176813	3.16702	3
-1.781871	9.097953	2
-0.566606	5.749003	3
0.931635	1.589505	1
-0.024205	6.151823	3
-0.036453	2.690988	1
-0.196949	0.444165	1
1.014459	5.754399	3
1.985298	3.230619	3
-1.693453	-0.55754	1
-0.576525	11.778922	2
-0.346811	-1.67873	1
-2.124484	2.672471	1
1.217916	9.597015	0
-0.733928	9.098687	0
-3.642001	-1.618087	1
0.315985	3.523953	3
1.416614	9.619232	0
-0.386323	3.989286	3
0.556921	8.294984	0
1.224863	11.58736	2
-1.347803	-2.406051	1
1.196604	4.951851	3
0.275221	9.543647	0
0.470575	9.332488	0
-1.889567	9.542662	2
-1.527893	12.150579	2
-1.185247	11.309318	2
-0.445678	3.297303	3
1.042222	6.105155	3
-0.618787	10.320986	2
1.152083	0.548467	1
0.828534	2.676045	3
-1.237728	10.549033	2
-0.683565	-2.166125	1
0.229456	5.921938	3
-0.959885	11.555336	2
0.492911	10.993324	2
0.184992	8.721488	0
-0.355715	10.325976	2
-0.397822	8.058397	0
0.824839	13.730343	2
1.507278	5.027866	3
0.099671	6.835839	3
-0.344008	10.717485	2
1.785928	7.718645	0
-0.918801	11.560217	2
-0.364009	4.7473	3
-0.841722	4.119083	3
0.490426	1.960539	1
-0.007194	9.075792	0
0.356107	12.447863	2
0.342578	12.281162	2
-0.810823	-1.466018	1
2.530777	6.476801	3
1.296683	11.607559	2
0.475487	12.040035	2
-0.783277	11.009725	2
0.074798	11.02365	2
-1.337472	0.468339	1
-0.102781	13.763651	2
-0.147324	2.874846	3
0.518389	9.887035	0
1.015399	7.571882	0
-1.658086	-0.027255	1
1.319944	2.171228	1
2.056216	5.019981	3
-0.851633	4.375691	3
-1.510047	6.061992	3
-1.076637	-3.181888	1
1.821096	10.28399	0
3.01015	8.401766	0
-1.099458	1.688274	1
-0.834872	-1.733869	1
-0.846637	3.849075	3
1.400102	12.628781	2
1.752842	5.468166	3
0.078557	0.059736	1
0.089392	-0.7153	1
1.825662	12.693808	2
0.197445	9.744638	0
0.126117	0.922311	1
-0.679797	1.22053	1
0.677983	2.556666	1
0.761349	10.693862	0
-2.168791	0.143632	1
1.38861	9.341997	0
0.317029	14.739025	2
-2.65887965178	0.658328066452	1
-2.30615885683	11.5036718065	2
-2.83005963556	7.30810428189	3
-2.30319006285	3.18958964564	1
-2.31349250532	4.41749905123	3
-2.71157223048	0.21599278192	1
-2.99935111344	14.5766538514	2
-2.50329272687	12.7274016382	2
-2.14191210185	9.75999136268	2
-2.21409612618	9.25234159289	2
-2.0503599261	1.87312594247	1
-2.99747377006	2.82404034943	1
-2.39019233623	1.88778487771	1
-2.00981101171	13.0015287952	2
-2.06105014551	7.26924117028	3
-2.94028883652	10.8418044558	2
-2.56811396636	1.31240093493	1
-2.89942462914	7.47932555859	3
-2.83349151782	0.292728283929	1
-2.16467022383	4.62184237142	3
2.02604290795	6.68200376515	3
2.3755881562	9.3838379637	0
2.48299208843	9.75753701005	0
2.65108044441	9.39059526201	0
2.49422603944	11.856131521	0
2.47215954581	4.83431641068	3
2.26731525725	5.64891602081	3
2.33628075296	10.4603294628	0
2.4548064459	9.90879879651	0
2.13147505967	8.99561368732	0
2.86925733903	4.26531919929	3
2.05715970133	4.97240425903	3
2.14839753847	8.91032469409	0
2.17630437606	5.76122354509	3
2.86205491781	11.630342945	0

使用softmax_regression_train.py对上述数据进行训练：

# coding:UTF-8
import numpy as np

def load_data(inputfile):
    '''导入训练数据
    input:  inputfile(string)训练样本的位置
    output: feature_data(mat)特征
            label_data(mat)标签
            k(int)类别的个数
    '''
    f = open(inputfile)  # 打开文件
    feature_data = []
    label_data = []
    for line in f.readlines():
        feature_tmp = []
        feature_tmp.append(1)  # 偏置项
        lines = line.strip().split("\t")
        for i in xrange(len(lines) - 1):
            feature_tmp.append(float(lines[i]))
        label_data.append(int(lines[-1]))
        
        feature_data.append(feature_tmp)
    f.close()  # 关闭文件
    return np.mat(feature_data), np.mat(label_data).T, len(set(label_data))

def cost(err, label_data):
    '''计算损失函数值
    input:  err(mat):exp的值
            label_data(mat):标签的值
    output: sum_cost / m(float):损失函数的值
    '''
    m = np.shape(err)[0]
    sum_cost = 0.0
    for i in xrange(m):
        if err[i, label_data[i, 0]] / np.sum(err[i, :]) > 0:
            sum_cost -= np.log(err[i, label_data[i, 0]] / np.sum(err[i, :]))
        else:
            sum_cost -= 0
    return sum_cost / m
    

def gradientAscent(feature_data, label_data, k, maxCycle, alpha):
    '''利用梯度下降法训练Softmax模型
    input:  feature_data(mat):特征
            label_data(mat):标签
            k(int):类别的个数
            maxCycle(int):最大的迭代次数
            alpha(float):学习率
    output: weights(mat)：权重
    '''
    m, n = np.shape(feature_data)
    weights = np.mat(np.ones((n, k)))  # 权重的初始化
    i = 0
    while i <= maxCycle:
        err = np.exp(feature_data * weights)
        if i % 500 == 0:
            print "\t-----iter: ", i , ", cost: ", cost(err, label_data)
        rowsum = -err.sum(axis=1)
        rowsum = rowsum.repeat(k, axis=1)
        err = err / rowsum
        for x in range(m):
            err[x, label_data[x, 0]] += 1
        weights = weights + (alpha / m) * feature_data.T * err      
        i += 1           
    return weights

def save_model(file_name, weights):
    '''保存最终的模型
    input:  file_name(string):保存的文件名
            weights(mat):softmax模型
    '''
    f_w = open(file_name, "w")
    m, n = np.shape(weights)
    for i in xrange(m):
        w_tmp = []
        for j in xrange(n):
            w_tmp.append(str(weights[i, j]))
        f_w.write("\t".join(w_tmp) + "\n")
    f_w.close()
            
if __name__ == "__main__":
    inputfile = "SoftInput.txt"
    # 1、导入训练数据
    print "---------- 1.load data ------------"
    feature, label, k = load_data(inputfile)
    # 2、训练Softmax模型
    print "---------- 2.training ------------"
    weights = gradientAscent(feature, label, k, 10000, 0.4)
    # 3、保存最终的模型
    print "---------- 3.save model ------------"
    save_model("weights", weights)

产生随机数进行测试，测试脚本为softmax_regression_test.py：

# coding:UTF-8

import numpy as np
import random as rd

def load_weights(weights_path):
    '''导入训练好的Softmax模型
    input:  weights_path(string)权重的存储位置
    output: weights(mat)将权重存到矩阵中
            m(int)权重的行数
            n(int)权重的列数
    '''
    f = open(weights_path)
    w = []
    for line in f.readlines():
        w_tmp = []
        lines = line.strip().split("\t")
        for x in lines:
            w_tmp.append(float(x))
        w.append(w_tmp)
    f.close()
    weights = np.mat(w)
    m, n = np.shape(weights)
    return weights, m, n

def load_data(num, m):
    '''导入测试数据
    input:  num(int)生成的测试样本的个数
            m(int)样本的维数
    output: testDataSet(mat)生成测试样本
    '''
    testDataSet = np.mat(np.ones((num, m)))
    for i in xrange(num):
        testDataSet[i, 1] = rd.random() * 6 - 3#随机生成[-3,3]之间的随机数
        testDataSet[i, 2] = rd.random() * 15#随机生成[0,15]之间是的随机数
    return testDataSet

def predict(test_data, weights):
    '''利用训练好的Softmax模型对测试数据进行预测
    input:  test_data(mat)测试数据的特征
            weights(mat)模型的权重
    output: h.argmax(axis=1)所属的类别
    '''
    h = test_data * weights
    return h.argmax(axis=1)#获得所属的类别

def save_result(file_name, result):
    '''保存最终的预测结果
    input:  file_name(string):保存最终结果的文件名
            result(mat):最终的预测结果
    '''
    f_result = open(file_name, "w")
    m = np.shape(result)[0]
    for i in xrange(m):
        f_result.write(str(result[i, 0]) + "\n")
    f_result.close()
    

if __name__ == "__main__":
    # 1、导入Softmax模型
    print "---------- 1.load model ------------"
    w, m , n = load_weights("weights")
    # 2、导入测试数据
    print "---------- 2.load data ------------"
    test_data = load_data(4000, m)
    # 3、利用训练好的Softmax模型对测试数据进行预测
    print "---------- 3.get Prediction ------------"
    result = predict(test_data, w)
    # 4、保存最终的预测结果
    print "---------- 4.save prediction ------------"
    save_result("result", result)
    

训练的结果为：

通过训练，得到了最终的模型的参数，模型的参数保存在文件weights中，其中参数为：

在本次测试中随机生成了4000个样本，目的是为了能够更好地刻画出分类的边界，最终的分类效果如图所示（使用matplotlib绘图，代码略）：

图中，通过点的不同深浅区分出4个类别之间的边界。

参考

Python机器学习算法/赵志勇著.——北京：电子工业出版社，2017.7