机器学习方法（五）：逻辑回归Logistic Regression，Softmax Regression

欢迎转载，转载请注明：本文出自Bin的专栏blog.csdn.net/xbinworld。
技术交流QQ群：433250724，欢迎对算法、技术、应用感兴趣的同学加入。

前面介绍过线性回归的基本知识，线性回归因为它的简单，易用，且可以求出闭合解，被广泛地运用在各种机器学习应用中。事实上，除了单独使用，线性回归也是很多其他算法的组成部分。线性回归的缺点也是很明显的，因为线性回归是输入到输出的线性变换，拟合能力有限；另外，线性回归的目标值可以是(−∞,+∞)，而有的时候，目标值的范围是[0,1]（可以表示概率值），那么就不方便了。

逻辑回归可以说是最为常用的机器学习算法之一，最经典的场景就是计算广告中用于CTR预估，是很多广告系统的核心算法。

逻辑回归Logistic Regression

逻辑回归(LR)，虽然叫回归，然是从目标函数来看，它是设计用来做分类的，经典的LR是用于二分类的情况的，也就是说只有0,1两类。

定义一个样本xi∈Rm的类别是1的概率为：

P(yi=1|xi)=exp(wTxi)1+exp(wTxi)=11+exp(−wTxi)

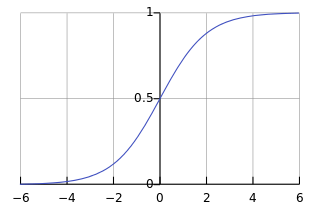
这就是sigmoid函数的形式，绘制出来是这样的形式：
、
图1

可以看到，取值范围是在(0,1)的，因此近似可以理解为一个概率的取值。在神经网络模型中，sigmoid函数是一种激励函数，其他常见的还有tanh函数，以及其他一些函数。（这些激励函数后面介绍神经网络模型的时候再展开）

记sigmoid函数为

h(xi)=P(yi=1|xi)=11+exp(−wTxi)

给定一个数据集S，其中有N个样本，那么可以写出目标函数：最小化负对数似然函数：

minwL(w)=−log∏i=1Nh(xi)yi（1−h(xi))1−yi=−∑i=1N[yilogh(xi)+(1−yi)log(1−h(xi))]=−∑i=