梯度下降方法是目前最流行的神经网络优化方法,并且现在主流的深度学习框架(tensorflow,caffe,keras,MXNET等)都包含了若干种梯度下降迭代优化器。我们在搭建网络的时候,基本都是拿它们封装好的函数直接用。实际上这些算法在不同情况可能有很大的性能差异,弄清楚它们的原理差异,有助于我们分析。
参考文章:梯度下降优化方法总结
梯度下降(gradient descent,GD)是最基础的概念,它有三个很近似的名词:
批量梯度下降(Batch gradient descent)
每次使用整个训练集计算目标函数的梯度,
因为每更新一次参数就需要计算整个数据集,所以批量梯度下降算法十分缓慢而且难以存放在内存中计算,且无法在线更新。
随机梯度下降(stochastic gradient descent, SGD)
一次只使用一个样本计算目标函数的梯度,
因为每次只计算一个样本,所以SGD计算非常快且适合线上更新模型。SGD频繁地参数更新可以使算法跳出局部最优点,更可能寻找到接近全局最优的解,但也因频繁地更新参数使得目标函数抖动非常厉害。
小批量梯度下降(mini-batch gradient descent)
结合了BGD和SGD的优点,一次以小批量的训练数据计算目标函数的梯度,
n为每批训练集的数量。
优点:1. 相比较SGD增加了每次更新使用的训练数据量,使得目标函数收敛得更加平稳。2. 可以使用矩阵操作对每批数据进行计算,提升了计算效率。
这三种的区别仅是每次计算使用的样本数量不同,没有对步长η或梯度变化量▽J作改进。
---------------------------------------------------------------------------------------------------------------------------
然后是一些梯度下降优化算法:
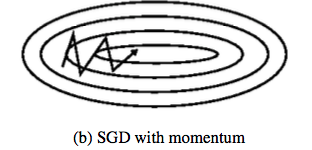
Momentum方法
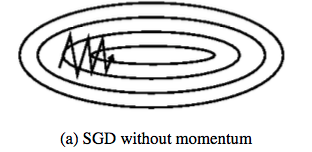
目标函数一般在不同维度上的梯度相差很大,就如下图的等高线在y方向上很密集(梯度变化大)所以震荡频繁,而x方向缓慢移动。
因为y方向在摇摆时梯度方向相反,前后两次相加就可以一定程度抵消,x方向梯度变化是累加的,效果就是接近最优点的速度加快。
这个方法计算当前步的下降距离时纳入了前一步的下降距离vt-1(有关前一步的梯度方向),就是冲量项(γvt-1),而步长η没有变化。
---------------------------------------------------------------------------------------------------------------------------
然后下面是一些改变了步长的梯度下降优化算法:
Adagrad方法
对稀疏特征采用高的更新速率,而对其他特征采用相对较低的更新速率。与前面使用相同的学习速率η更新所有的参数不同,Adagrad对每个参数使用不同的步长进行更新。
用gt,i来表示参数θi在第t次更新时的梯度,
而Adagrad的更新表达式可以写为,
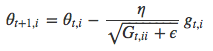
其中,⨀表示矩阵和向量的乘积,Gt中的第i行第i列数表示θi的从过去到现在的梯度平方和。
这个方法利用参数的稀疏性来调整学习率,缺点是Gt累加了历史的梯度平方,学习率就会变得越来越小,最后无法再学习到新的信息。
AdaDelta方法
主要解决了Adagrad算法中学习率衰减过快的问题,它不再累加参数所有的历史梯度平方和,转而设定一个窗口w,只求前w个历史梯度平方的平均数(γ加权平均),
AdaDelta的更新表达式可以写为,
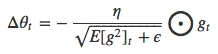
Rprop方法(Resilient Propagation)
设定权重变化的加减速因子d,比较本次梯度变化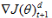
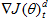
如果两次梯度符号相反,则抑制参数变化 (η-<1)
如果两次梯度符号相同,则增强参数变化 (η+>1)
RMSprop方法(Root Mean Square Propagation)
类似于一种特殊的简化的Adadelta形式,
Adam方法(Adaptive Moment Estimation)
它也是一种自适应学习率方法,与Adadelta和RMSprop类似,它将每个参数的历史梯度平方均值存于vt中,不同的是,Adam还使用了类似冲量的衰减项mt,
Adam的更新表达式可以写为,
参考文章里说建议β1设0.9,β2设0.999。








 本文详细介绍了深度学习中的梯度下降优化算法,包括批量梯度下降、随机梯度下降、小批量梯度下降及其优缺点。进一步探讨了Momentum、Adagrad、AdaDelta、Rprop、RMSprop和Adam等改进方法,阐述了它们如何调整学习率和处理梯度问题,以提高模型训练的效率和性能。
本文详细介绍了深度学习中的梯度下降优化算法,包括批量梯度下降、随机梯度下降、小批量梯度下降及其优缺点。进一步探讨了Momentum、Adagrad、AdaDelta、Rprop、RMSprop和Adam等改进方法,阐述了它们如何调整学习率和处理梯度问题,以提高模型训练的效率和性能。
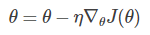
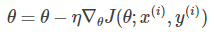
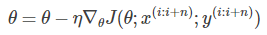
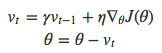
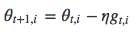
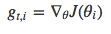

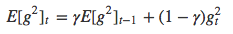
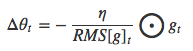
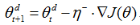
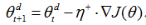
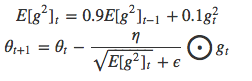
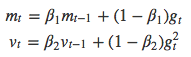
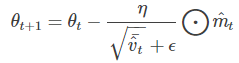

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








