【笔记】莫比乌斯反演-从入门到入土

上一篇：莫比乌斯反演（前置知识）

本篇文章主要为莫比乌斯反演的基本讲解，附以一小部分的狄利克雷卷积辅助理解。

莫比乌斯反演

正片开始

关于反演

顾名思义，反演就是反向演变，举个栗子，若有$F(n)=k\cdot f(n)$，我们能够推出$f(n)=\frac{F(n)}{k}$，这就是反演。

莫比乌斯函数

定义

$\mu (n)=\{\begin{array}{ll}1& n=1\\ (-1{)}^k& n=p_1{p}_2\dots p_k(p_i\in P)\\ 0& p^2|n(p\in P)\end{array}$

性质

$$\sum _{d|n}\mu (d)=[n=1]$$
证明：
当$n=1$时显然。
考虑$\mu (d)$的贡献。
只有当$d$中的质因子都只出现一次时，$\mu (d)$才对和式有贡献。
问题变成了在$n$的质因子中选择$k$个，$k$为奇数则贡献为$-1$，$k$为偶数则贡献为$1$.
设$n$中有$m$种不同的质因子。
$$\sum _{d|n}\mu (d)=\sum _{j=0}^m(-1{)}^j\left(\begin{array}{c}m\\ j\end{array}\right)$$
$\left(\begin{array}{c}m\\ j\end{array}\right)$表示在$m$个不同的数中选取$j$个数的方案数，等价于$C_m^j$.
根据二项式定理$(x+y{)}^n=\sum _{i=0}^n\left(\begin{array}{c}n\\ i\end{array}\right)x^i{y}^{n-i}$，我们令$x=-1,y=1$，就可以发现右边的和式等于$\sum _{j=0}^m(-1{)}^j\left(\begin{array}{c}m\\ j\end{array}\right)$，所以有
$$\sum _{d|n}\mu (d)=\sum _{j=0}^m(-1{)}^j\left(\begin{array}{c}m\\ j\end{array}\right)=(1-1{)}^m=0$$
得证。

这就是说，当$n=1$时$\sum _{d|n}\mu (d)=1$，否则$\sum _{d|n}\mu (d)=0$.

莫比乌斯反演公式

公式1

若$F(n)=\sum _{d|n}f(d)$，则$f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})$
证明：
$\sum _{d|n}\mu (d)F(\frac{n}{d})=\sum _{d|n}\mu (d)\sum _{p|\frac{n}{d}}f(p)$
注意此时的运算顺序是$\sum _{d|n}(\mu (d)\sum _{p|\frac{n}{d}}f(p))$
这时候，我们可以手玩这个式子，来寻找规律。
我们让$n=6$.
$$\begin{gathered} \sum _{d|n}\mu (d)\sum _{p|\frac{n}{d}}f(p) \\ =\sum _{d|6}\mu (d)\sum _{p|\frac{6}{d}}f(p) \\ =\mu (1)\times (f(1)+f(2)+f(3)+f(6)) \\ +\mu (2)\times (f(1)+f(3)) \\ +\mu (3)\times (f(1)+f(2)) \\ +\mu (6)\times f(1) \\ =f(1)\times (\mu (1)+\mu (2)+\mu (3)+\mu (6)) \\ +f(2)\times (\mu (1)+\mu (3)) \\ +f(3)\times (\mu (1)+\mu (2)) \\ +f(6)\times \mu (1) \\ =\sum _{d|6}f(d)\sum _{p|\frac{6}{d}}\mu (p) \\ =\sum _{d|n}f(d)\sum _{p|\frac{n}{d}}\mu (p) \end{gathered}$$
感性证明

这貌似不是巧合，其中肯定有什么规律。
思考为什么有$\sum _{d|n}\mu (d)\sum _{p|\frac{n}{d}}f(p)=\sum _{p|n}f(p)\sum _{d|\frac{n}{p}}\mu (d)$
观察原式的枚举变量，容易发现$pd|n$，且$p|n,d|n$
原式可以理解为枚举$\mu (d)$，计算出现了多少个$\mu (d)$
而转化后的式子是枚举$f(p)$，计算出现了多少个$f(p)$
那么有哪些$\mu$值对$f(p)$有贡献呢？
换句话说，哪些$\mu$值的和才是$f(p)$的系数呢？
因为$pd|n$，所以$d|\frac{n}{p}$. 满足这条性质的$\mu (d)$值之和就是$f(p)$的系数。
于是完成证明$\sum _{d|n}\mu (d)F(\frac{n}{d})=\sum _{p|n}f(p)\sum _{d|\frac{n}{p}}\mu (d)$
根据莫比乌斯函数的性质，只有当$\frac{n}{p}=1$时，$f(p)\sum _{d|\frac{n}{p}}\mu (d)$ 才不为$0$，因为$\sum _{d|\frac{n}{p}}\mu (d)=[\frac{n}{p}=1]$.
此时$n=p$.
也就是只有在$p=n$时才会对$\sum _{p|n}f(p)\sum _{d|\frac{n}{p}}\mu (d)$这个式子产生贡献。
所以$\sum _{p|n}f(p)\sum _{d|\frac{n}{p}}\mu (d)=f(n)$.
于是得证。

公式2

若$F(n)=\sum _{n|d}f(d)$，则$f(n)=\sum _{n|d}\mu (\frac{d}{n})F(d)$
证明：
思路同上，稍复杂。
$\sum _{n|d}\mu (\frac{d}{n})F(d)=\sum _{n|d}\mu (\frac{d}{n})\sum _{d|p}f(p)$
仍然可以手玩$n=6$的栗子，需要注意的是这里的项数有无限个。
手玩过程略，以下是理论简单证明。
已知$n|d|p$，设$d=kn$，显然$kn|p$.
$\sum _{n|d}\mu (\frac{d}{n})\sum _{d|p}f(p)=\sum _{k=1}^{\infty }\mu (k)\sum _{kn|p}f(p)$
考虑$f(p)$的系数。
因为$kn|p$，所以$k|\frac{p}{n}$.
所以$\sum _{k=1}^{\infty }\mu (k)\sum _{kn|p}f(p)=\sum _{n|p}f(p)\sum _{d|\frac{p}{n}}\mu (d)$
对$\sum _{d|\frac{p}{n}}\mu (d)$的讨论同上，最终得出$\sum _{n|p}f(p)\sum _{d|\frac{p}{n}}\mu (d)=f(n)$
得证。

整除分块

引入

先看一个问题：求$\sum _{i=1}^n\lfloor \frac{n}{i}\rfloor$的值，$1\le n\le 10^{12}$.
暴力显然，时间复杂度为$O(n)$，无法通过这题。

关于整除分块

整除分块，又称数论分块，能够在$O(\sqrt{n})$的时间复杂度内解决引入中的问题。

其原理是不同的数做整除运算时可能有相同的结果，利用这一点合理分块，大大降低时间复杂度。
对一个整除和式分成多个块，故称整除分块。

只可用于整除式。

学习整除分块，是因为莫比乌斯反演中很多和式最后都会带有整除和式，运用整除分块就可以非常快速地求出整除和式的值。

这篇博客的整除分块写得很好，可以说是全网最详细了。

基础推导

首先观察下表。

x	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$y=\lfloor \frac{20}{x}\rfloor$	20	10	6	5	4	3	2	2	2	2	1	1	1	1	1	1	1	1	1	1

显然，$y=\lfloor \frac{n}{x}\rfloor$的函数值是单调递减的，$\lfloor \frac{n}{x}\rfloor$相同的$x$一定是连续的。
举个栗子，上表中$y=\lfloor \frac{20}{x}\rfloor$的值为$2$的$x$是$7$到$10$这一连续段。
对于上表，计算$\sum _{x=1}^{20}\lfloor \frac{20}{x}\rfloor$的值，除了可以暴力计算外，还可以$20\times 1+10\times 1+6\times 1+5\times 1+4\times 1+3\times 1+2\times 4+1\times 10$.
这就是整除分块的基本思想，把$\lfloor \frac{n}{x}\rfloor$值相同的$x$分成一块，用块长乘块值得到这个块的贡献。
那么为什么其时间复杂度为$O(\sqrt{n})$呢？
我们要充分发挥数形结合的数学思想，就可以巧妙地不严谨证明了。
观察下图，这是$y=\frac{10}{x}$的函数图像，$C$点为$(\sqrt{10},\sqrt{10})$。
显然，这个函数图像关于直线$y=x$对称。
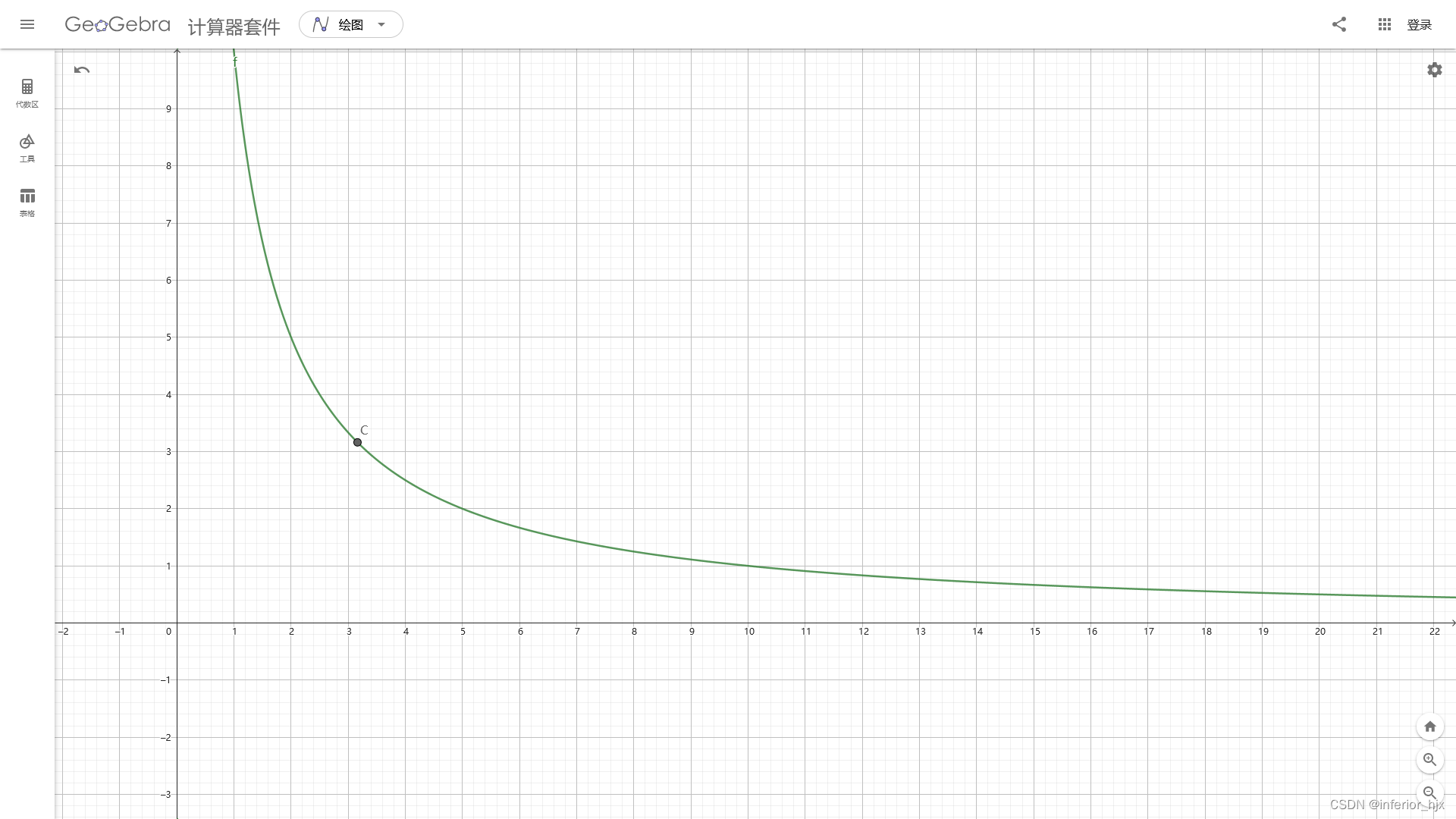那么在$C$点左侧，有$\sqrt{n}$个整数$x$，那么最多有$\sqrt{n}$个整点。
那么将函数图像沿直线$y=x$翻折，得到$C$点右侧也最多有$\sqrt{n}$个整点。显然，$C$点右侧的整点的纵坐标$y$值只有$\sqrt{n}$个取值。
所以总共最多有$2\sqrt{n}$个整点，分块后计算的时间复杂度为$O(\sqrt{n})$.

那么我们如何计算块长乘块值呢？
假设我们知道一个块的左端点$l$，显然块值$k=\lfloor \frac{n}{l}\rfloor$.
如何求右端点$r$?
可以发现，块内的值$i$满足$ik\le n$，即$i\le \lfloor \frac{n}{k}\rfloor$，$r$就是$i$的最大值，即$r=\lfloor \frac{n}{k}\rfloor$。
因为$k=\lfloor \frac{n}{l}\rfloor$，所以$r=\lfloor \frac{n}{k}\rfloor =\lfloor \frac{n}{\lfloor \frac{n}{l}\rfloor }\rfloor$
这就是最基础的整除分块。

简单扩展

求
$$\sum _{i=1}^{min(n,m)}\lfloor \frac{n}{i}\rfloor \lfloor \frac{m}{i}\rfloor$$
这个式子很重要，很多莫反的题目最后都包含这个式子。
其实非常简单，对于这个式子，仍然有$\lfloor \frac{n}{i}\rfloor$和$\lfloor \frac{m}{i}\rfloor$的值都分别相等的一段$x$.
不懂的话像上面一样列表即可发现。
一个块的右端点就是对$\lfloor \frac{n}{i}\rfloor$整除分块的右端点和对$\lfloor \frac{m}{i}\rfloor$整除分块的右端点的较小值。
具体见代码。

for(int i = 1; i <= min(n, m);) {
    int l = i, r = min(n / (n / i), m / (m / i));
    ans += 1ll * (n / l) * (m / l) * (r - l + 1), i = r + 1;
}

更多关于整除分块的探讨在上文提到的文章中有写到。

莫比乌斯反演的应用

例1：证明下式成立

$$\sum _{d|n}\mu (d)\frac{n}{d}=\varphi (n)$$
证明：
设
$$F(n)=n,f(n)=\varphi (n)$$
因为$n=\sum _{d|n}\varphi (d)$，所以$F(n)=\sum _{d|n}f(d)$.
使用公式1反演$f(n)$，得
$$\varphi (n)=f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})=\sum _{d|n}\mu (d)\frac{n}{d}$$

例2：YY的GCD

题目
题目大意：给定$n,m(1\le n,m\le 10^7)$，求$\sum _{i=1}^n\sum _{j=1}^m[(i,j)\in P]$，有$C(1\le T\le 10^4)$次询问。
设$f(p)$为二元组$(x,y)$在各自的值域范围内满足$(x,y)=p$的二元组数量，即$f(p)=\sum _{i=1}^n\sum _{j=1}^m[(x,y)=p]$
设$F(p)$为二元组$(x,y)$在各自的值域范围内满足$p|(x,y)$的二元组数量，即$F(p)=\sum _{i=1}^n\sum _{j=1}^m[p|(x,y)]$
设$P$为区间$[1,min(n,m)]$内的质数集合。
有
$F(p)=\sum _{p|d}f(d)$，所以$f(p)=\sum _{p|d}\mu (\frac{d}{p})F(d)$
$F(1)=\sum _{p\le n}f(p)$，$f(1)=\sum _{d=1}^{\infty }\mu (d)F(d)$

答案就是
$$\sum _{p\in P,x\le n,y\le m}f(p)$$
因为$(x,y)=p$，所以计算$x\le \lfloor \frac{n}{p}\rfloor ,y\le \lfloor \frac{m}{p}\rfloor$范围内$(x,y)=1$的值与原式的值等价。
$$\begin{gathered} \sum _{p\in P,x\le n,y\le m}f(p) \\ =\sum _{p\in P,x\le \frac{n}{p},y\le \frac{m}{p}}f(1) \\ =\sum _{p\in P,x\le \frac{n}{p},y\le \frac{m}{p},1|d}F(d)\mu (d) \end{gathered}$$
推导$F(p)=\sum _{i=1}^n\sum _{j=1}^m[p|(x,y)]=\sum _{i=1}^{\lfloor \frac{n}{p}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{p}\rfloor }[1|(x,y)]=\lfloor \frac{n}{p}\rfloor \times \lfloor \frac{m}{p}\rfloor$，注意这里的$x,y$取值分别是$n,m$之内。
所以
$$\sum _{p\in P,x\le \frac{n}{p},y\le \frac{m}{p},1|d}F(d)\mu (d)=\sum _{p\in P,x\le \frac{n}{p},y\le \frac{m}{p},1|d}\mu (d)\lfloor \frac{n}{pd}\rfloor \times \lfloor \frac{m}{pd}\rfloor$$
这里$n$要多除以一个$p$的原因是$F(d)$中的二元组$(x,y)$的范围是$\lfloor \frac{n}{p}\rfloor ,\lfloor \frac{m}{p}\rfloor$.
令$T=pd$，则
$$\sum _{p\in P,x\le \frac{n}{p},y\le \frac{m}{p},1|d}\mu (d)\lfloor \frac{n}{pd}\rfloor \times \lfloor \frac{m}{pd}\rfloor =\sum _{p\in P,T\le min(n,m)}\mu (\frac{T}{p})\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor$$
考虑对于$\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor$求其系数，容易发现系数为$\sum _{p|T}\mu (\frac{T}{p})$
则
$$\sum _{p\in P,T\le min(n,m)}\mu (\frac{T}{p})\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor =\sum _{T\le min(n,m)}\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor \sum _{p|T}\mu (\frac{T}{p})$$
对于$\lfloor \frac{n}{T}\rfloor \lfloor \frac{m}{T}\rfloor$，可以用整除分块，对于后面的$\sum _{p|T}\mu (\frac{T}{p})$可以预处理出前缀和来计算。
首先线性筛出所有$\mu$函数的值，然后枚举质数$p$，再枚举其倍数$\frac{T}{p}$，将$\mu (\frac{T}{p})$的值累加到$sum[T]$中。
这样计算看起来很慢，但其实是很快的。
这样计算的时间复杂度为$\sum _{p|T}(\frac{T}{p})=T\sum _{p|T}\frac{1}{p}<T\sum _{x=1}^T\frac{1}{x}<T\ln T$
所以每个质数均摊的时间复杂度为$O(\ln T)$，而质数个数有$\frac{T}{\ln T}$个，所以预处理的时间复杂度为$O(T)$
通过整除分块，每组数据可以在$O(\sqrt{n})$的时间复杂度内计算，所以总的时间复杂度为$O(C\sqrt{n})$

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10000005;
int T, n, m, mu[N], smu[N], vis[N], pri[N], cnt = 0;
void getmu() {
    mu[1] = 1;
    for (int i = 2; i < N; i++) {
        if (!vis[i]) pri[++cnt] = i, mu[i] = -1;
        for (int j = 1; j <= cnt && i * pri[j] < N; j++) {
            vis[i * pri[j]] = 1;
            if (i % pri[j] == 0) break;
            mu[i * pri[j]] = -mu[i];
        }
    }
}
void getsmu() {
    for (int i = 1; i <= cnt; i++)
        for (int j = 1; pri[i] * j < N; j++)
            smu[pri[i] * j] += mu[j];
    for (int i = 2; i < N; i++) smu[i] += smu[i - 1];
}
int main() {
    scanf("%d", &T);
    getmu(), getsmu();
    while (T--) {
        scanf("%d%d", &n, &m);
        LL ans = 0;
        for (int i = 1; i <= min(n, m);) {
            int l = i, r = min(n / (n / i), m / (m / i));
            ans += 1ll * (smu[r] - smu[l - 1]) * (n / l) * (m / l), i = r + 1;
        }
        printf("%lld\n", ans);
    }
    return 0;
}

例3：Problem b

题目
题目大意：对于给定的$a,b,c,d,k$，求$\sum _{x=a}^b\sum _{y=c}^d[(x,y)=k]$. 有$N$次询问。

设$$\begin{gathered} f_{n,m}(k)=\sum _{x=1}^n\sum _{y=1}^m[(x,y)=k] \\ {F}_{n,m}(k)=\sum _{x=1}^n\sum _{y=1}^m[k|(x,y)] \end{gathered}$$
有$$F_{A,B}(k)=\sum _{k|n}{f}_{A,B}(n)$$
则答案为$f_{b,d}(k)-f_{a-1,d}(k)-f_{b,c-1}(k)+f_{a-1,c-1}(k)$，类似于二维前缀和的容斥。

$F_{n,m}(k)$是很好求的，它等于$\lfloor \frac{n}{k}\rfloor \lfloor \frac{m}{k}\rfloor$.

这是因为在$n$内有$\lfloor \frac{n}{k}\rfloor$个数包含因子$k$，同理，在$m$内有$\lfloor \frac{m}{k}\rfloor$个数包含因子$k$.

根据乘法原理，有$\lfloor \frac{n}{k}\rfloor \lfloor \frac{m}{k}\rfloor$对二元组$(x,y)$满足$k|gcd(x,y)$.

运用莫反，有$f(n{)}_{A,B}=\sum _{n|k}\mu (\frac{k}{n})F_{A,B}(k)=\sum _{n|k}\mu (\frac{k}{n})\lfloor \frac{A}{k}\rfloor \lfloor \frac{B}{k}\rfloor$
令$T=\frac{k}{n}$，有
$$f(n{)}_{A,B}=\sum _{n|k}\mu (\frac{k}{n})\lfloor \frac{A}{k}\rfloor \lfloor \frac{B}{k}\rfloor =\sum _{T=1}^{min(A,B)}\mu (T)\lfloor \frac{A}{Tn}\rfloor \lfloor \frac{B}{Tn}\rfloor$$

运用整除分块+预处理，时间复杂度可以做到$O(N\sqrt{n})$，$n$最大为$5\times 10^4$.

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50005;
int T, a, b, c, d, k, vis[N], pri[N], cnt = 0, mu[N], sum[N];
void getmu() {
    mu[1] = 1;
    for (int i = 2; i < N; i++) {
        if (!vis[i]) pri[++cnt] = i, mu[i] = -1;
        for (int j = 1; j <= cnt && i * pri[j] < N; j++) {
            vis[i * pri[j]] = 1;
            if (i % pri[j] == 0) break;
            mu[i * pri[j]] = -mu[i];
        }
    }
    for (int i = 1; i < N; i++) sum[i] = sum[i - 1] + mu[i];
}
LL getans(int x, int y) {
    LL s = 0;
    for (int i = 1; i <= min(x, y);) {
        LL l = i, r = min(x / (x / i), y / (y / i));
        s += 1ll * (sum[r] - sum[l - 1]) * (x / (l * k)) * (y / (l * k)), i = r + 1;
    }
    return s;
}
int main() {
    scanf("%d", &T);
    getmu();
    while (T--) scanf("%d%d%d%d%d", &a, &b, &c, &d, &k), printf("%lld\n", getans(b, d) - getans(b, c - 1) - getans(a - 1, d) + getans(a - 1, c - 1));
    return 0;
}

例4：完全平方数

题目
题目大意：正整数集合中，若一个数是平方数（$1$ 除外）的正整数倍，称这个数为坏的数，否则为好的数。求第$K(1\le K\le 10^9)$个好的数。有$T(1\le T\le 50)$次询问。

这题实际上是莫比乌斯函数的巧妙运用。

如果我们知道$[1,n]$内有多少个好的数，就可以用二分解决。
考虑如何求$[1,n]$内有多少个好的数。
好的数不好直接求，转化为$n$减去坏的数的数量。
在区间$[1,n]$内有$\lfloor \frac{n}{4}\rfloor$个数为$2^2=4$的倍数，那当然不需要计算$\lfloor \frac{n}{16}\rfloor$的倍数。
所以只需要计算质数的倍数即可。
从而想到容斥。
从总数$n$中删去$4$的倍数，再删去$9$的倍数时，显然$36$的倍数被多删掉了，要加回来。
那么容斥的边界是什么呢？
对于质数$p$，显然其平方的倍数有$\lfloor \frac{n}{p^2}\rfloor$个。那么当$p$大于$\lfloor \sqrt{n}\rfloor$时，$\lfloor \frac{n}{p^2}\rfloor =0$. 所以容斥的边界为$p\le \lfloor \sqrt{n}\rfloor$.
前置知识中提到，莫比乌斯函数具有很好的容斥天赋，这题就是很好的体现。
当我们rp=max就可以想到坏的数的个数等于$\sum _{p\in P}^{\sqrt{n}}\mu (p)\lfloor \frac{n}{p^2}\rfloor$.
至此思路显然。
如果没有AC就把二分和$n$的上限往死里开。

时间复杂度为$O(T\sqrt{r_{max}}\log K)$，其中$r_{max}$表示二分的上限。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50005;
int T, k, mu[N], pri[N], cnt = 0, vis[N];
void getmu() {
    mu[1] = 1;
    for (int i = 2; i < N; i++) {
        if (!vis[i]) pri[++cnt] = i, mu[i] = -1;
        for (int j = 1; j <= cnt && i * pri[j] < N; j++) {
            vis[i * pri[j]] = 1;
            if (i % pri[j] == 0) break;
            mu[i * pri[j]] = -mu[i];
        }
    }
}
bool check(LL x) {
    LL sum = 0;
    for (LL i = 1; i <= sqrt(x); i++) sum += mu[i] * (x / (i * i));
    if (sum >= k) return false;
    return true;
}
int main() {
    scanf("%d", &T);
    getmu();
    while (T--) {
        scanf("%d", &k);
        LL ans = 0, l = 0, r = 2e9;
        while (l <= r) {
            LL mid = l + r >> 1;
            if (check(mid) == true) l = mid + 1;
            else r = mid - 1, ans = mid;
        }
        printf("%d\n", ans);
    }
    return 0;
}

例5：约数个数和

题目
题目大意：设$d(n)$为$n$的约数个数，给定$n,m(1\le n,m\le 50000)$，求$\sum _{i=1}^n\sum _{j=1}^{m}d(ij)$. 有$T$组询问。

设
$$\begin{gathered} f(k)=\sum _{i=1}^n\sum _{j=1}^m[(i,j)=k] \\ F(k)=\sum _{i=1}^n\sum _{j=1}^m[k|(i,j)]=\sum _{k|d}f(d) \end{gathered}$$
关于约数个数，有如下公式：
$$d(ij)=\sum _{x|i}\sum _{y|j}[(x,y)=1]$$
证明不会。手玩或许可以感性理解。
所以有
$$ans=\sum _{i=1}^n\sum _{j=1}^m\sum _{x|i}\sum _{y|j}[(x,y)=1]$$
因为$\sum _{d|n}=\mu (d)=[n=1]$，所以
$$\begin{gathered} ans=\sum _{i=1}^n\sum _{j=1}^m\sum _{x|i}\sum _{y|j}\sum _{d|(i,j)}\mu (d) \\ =\sum _{i=1}^n\sum _{j=1}^m\sum _{x|i}\sum _{y|j}\sum _{d=1}^{min(n,m)}\mu (d)\times [d|(x,y)] \end{gathered}$$
能够变换的原因是只有当$d|(x,y)$时才对$\mu (d)$有贡献。
对于每个$\mu (d)$，对其作出的贡献，即它的系数，为$\sum _{i=1}^n\sum _{j=1}^m\sum _{x|i}\sum _{y|j}[d|(x,y)]$.
所以有
$$ans=\sum _{d=1}^{min(n,m)}\mu (d)\sum _{i=1}^n\sum _{j=1}^m\sum _{x|i}\sum _{y|j}[d|(x,y)]$$
考虑直接枚举$x,y$，若有$d|(x,y)$，则有$i$的取值有$\lfloor \frac{n}{x}\rfloor$个，$j$的取值有$\lfloor \frac{m}{y}\rfloor$个。
所以有
$$ans=\sum _{d=1}^{min(n,m)}\mu (d)\sum _{x=1}^n\sum _{y=1}^m[d|(x,y)]\lfloor \frac{n}{x}\rfloor \lfloor \frac{m}{y}\rfloor$$
更换枚举项，设$x^{\prime }=dx,y^{\prime }=dy$，则
$$\begin{gathered} ans=\sum _{d=1}^{min(n,m)}\mu (d)\sum _{x^{\prime }=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{y^{\prime }=1}^{\lfloor \frac{m}{d}\rfloor }[d|(x^{\prime },y^{\prime })]\lfloor \frac{n}{d{x}^{\prime }}\rfloor \lfloor \frac{m}{d{y}^{\prime }}\rfloor \\ =\sum _{d=1}^{min(n,m)}\mu (d)\sum _{x^{\prime }=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{y^{\prime }=1}^{\lfloor \frac{m}{d}\rfloor }\lfloor \frac{n}{d{x}^{\prime }}\rfloor \lfloor \frac{m}{d{y}^{\prime }}\rfloor \end{gathered}$$
类比$\sum _{i=1}^a\sum _{j=1}^{b}ij=(\sum _{i=1}^{a}i)(\sum _{j=1}^{b}j)$，有
$$ans=\sum _{d=1}^{min(n,m)}\mu (d)(\sum _{x^{\prime }=1}^{\lfloor \frac{n}{d}\rfloor }\lfloor \frac{n}{d{x}^{\prime }}\rfloor )(\sum _{y^{\prime }=1}^{\lfloor \frac{m}{d}\rfloor }\lfloor \frac{m}{d{y}^{\prime }}\rfloor )$$
将$\sum _{i=1}^n\lfloor \frac{n}{i}\rfloor$花费$O(n\sqrt{n})$的时间整除分块预处理得到$sum[i]$，则
$$ans=\sum _{d=1}^{min(n,m)}\mu (d)sum[\frac{n}{d}]sum[\frac{m}{d}]$$
此时再对$\frac{n}{d},\frac{m}{d}$整除分块，每次询问的时间复杂度为$O(\sqrt{n})$. 加上$T$组询问，总的时间复杂度为$O(T\sqrt{n})$.

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50005;
int T, n, m, mu[N], vis[N], pri[N], cnt = 0;
LL f[N];
void getf() {
    for (int i = 1; i < N; i++)
        for (int l = 1, r; l <= i; l = r + 1) {
            r = i / (i / l);
            f[i] += 1ll * (r - l + 1) * (i / l);
        }
}
void getmu() {
    mu[1] = 1;
    for (int i = 2; i < N; i++) {
        if (!vis[i]) pri[++cnt] = i, mu[i] = -1;
        for (int j = 1; j <= cnt && i * pri[j] < N; j++) {
            vis[i * pri[j]] = 1;
            if (i % pri[j] == 0) break;
            mu[i * pri[j]] = -mu[i];
        }
    }
    for (int i = 2; i < N; i++) mu[i] += mu[i - 1];
}
int main() {
    getf(), getmu();
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &n, &m);
        LL ans = 0;
        for (int i = 1, r; i <= min(n, m); i = r + 1) {
            r = min(n / (n / i), m / (m / i));
            ans += 1ll * (mu[r] - mu[i - 1]) * f[n / i] * f[m / i];
        }
        printf("%lld\n", ans);
    }
    return 0;
}

总结

莫比乌斯反演能够将难以直接求解的函数转化为容易求解的函数求值。

莫比乌斯反演的题目大都有一个或多个和式，以及$gcd$，或者与$gcd$紧密相关的函数，如约数和函数$\sigma$.

莫比乌斯反演通常有如下步骤：

• 将原问题转化为类$\sum _{i=1}^n$的和式
• 设应求函数$f(n)$和易求函数$F(n)$，$F(n)$多与$gcd$有关，得到$F(n)$与$f(n)$的关系式和$F(n)$的易求形式
• 反演$f(n)$，得到和式，带入$F(n)$易求形式
• 和式除以$gcd$，消除$gcd$的影响
• 更换枚举顺序，分离$\sum$
• 更换枚举变量，将$\sum$的枚举变量变成连续的正整数，方法通常是设$d^{\prime }=\frac{n}{d}$或$\frac{d}{n}$
• 考虑整除分块及预处理，可能有杜教筛

第$3$到$6$步因人而异，可能有些没有，有些顺序不同。有时候一些步骤需要重复多次。

总的来说，莫比乌斯反演的题目就是和式的变换，AC这些题目的前提就是精通和式变换。

莫比乌斯反演要多练题才能对其有比较深入的理解。

狄利克雷卷积

定义

若有数论函数 $f,g,h$，满足 $h(n)=\sum _{d|n}f(d)g(\frac{n}{d})$，则称 $h$ 是 $f,g$ 的狄利克雷卷积，记为 $h=f\ast g$，一般读作“$f$ 卷 $g$”.

性质

1、交换律：

$$f\ast g=\sum _{d|n}f(d)g(\frac{n}{d})=\sum _{d|n}f(\frac{n}{d})g(d)=g\ast h$$

2、结合律：

设 $F=f\ast g,G=g\ast h$.

$$\begin{gathered} (f\ast g)\ast h=\sum _{d|n}F(d)h(\frac{n}{d}) \\ =\sum _{d|n}(\sum _{k|d}f(k)g(\frac{d}{k}))h(\frac{n}{d}) \end{gathered}$$

考虑提出 $f$，因为 $k|d|n$，有 $d|\frac{n}{k}$.

$$\sum _{d|n}(\sum _{k|d}f(k)g(\frac{d}{k}))h(\frac{n}{d})=\sum _{k|n}f(k)\sum _{d|\frac{n}{k}}g(d)h(\frac{n}{kd})=\sum _{k|n}f(k)G(\frac{n}{k})=f\ast (g\ast h)$$

单位元

单位元 $ϵ(n)=[n=1]$，容易证明任何数卷 $ϵ$ 都等于本身，其地位等同于乘法运算中的 $1$，加法运算中的 $0$.

常见狄利克雷卷积

$\mu \ast I=Id$

$\mu \ast Id=\varphi$

$\mu \ast \sigma =Id$

$Id\ast I=\sigma$

$\varphi \ast I=Id$

莫比乌斯反演与狄利克雷卷积有很密切的联系。

举个栗子：

$I(n)=\sum _{d|n}ϵ(d)=1$

依据莫比乌斯反演有 $ϵ(n)=\sum _{d|n}\mu (d)I(\frac{n}{d})=\mu \ast I$

狄利克雷卷积能够帮助我们更好地理解莫比乌斯反演。

总结

狄利克雷卷积实质上是一种和式的表示方式，非常简洁地表述了一串和式。

利用狄利克雷卷积可以和莫比乌斯反演互相推导，有利于我们理解莫反。