二维凸包 Andrew算法

凸包：二维平面内，给定n个散乱的点，求一个最小凸多边形（凸包），使得n个点都不在凸多边形外。

这里介绍 Andrew算法求解凸包

步骤：首先将点排序（x从小到大，如果x相同，y从小到大），删除重复点，到到点集p1,p2,...... 首先将p1,p2放进凸包里。从p3开始，当新节点在前进方向的左边时继续，否则依次删除最近加入到凸包中的点，直到新点在左边，具体如下图：

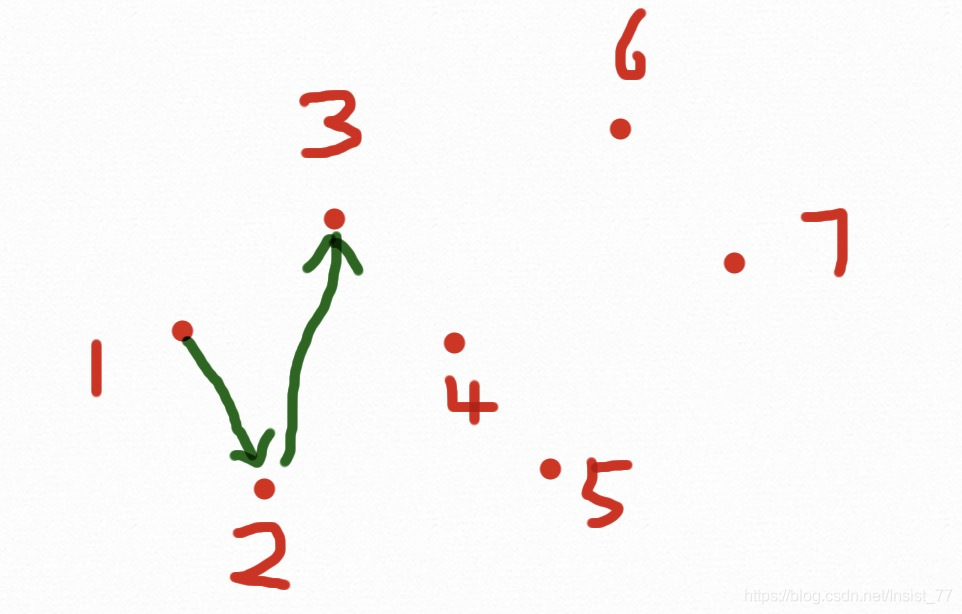
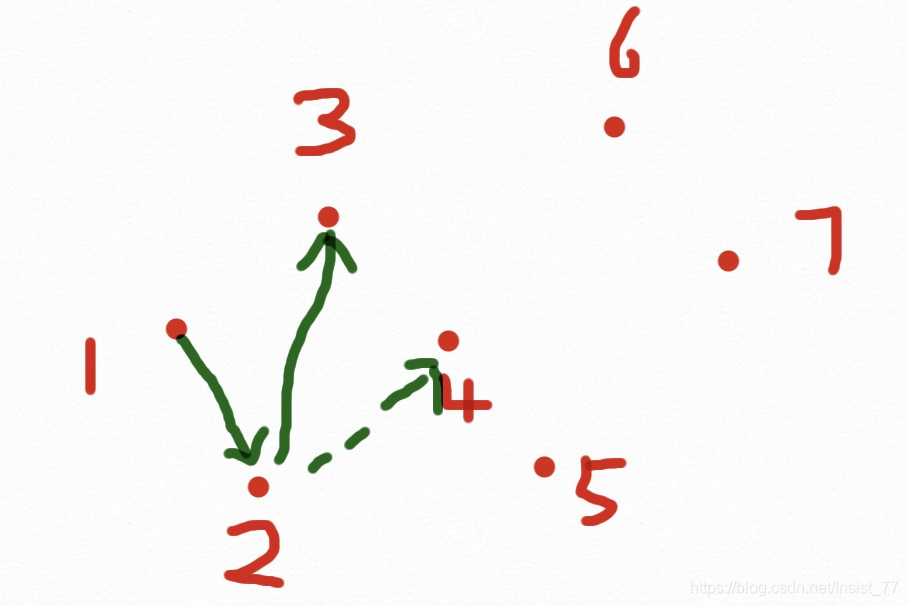
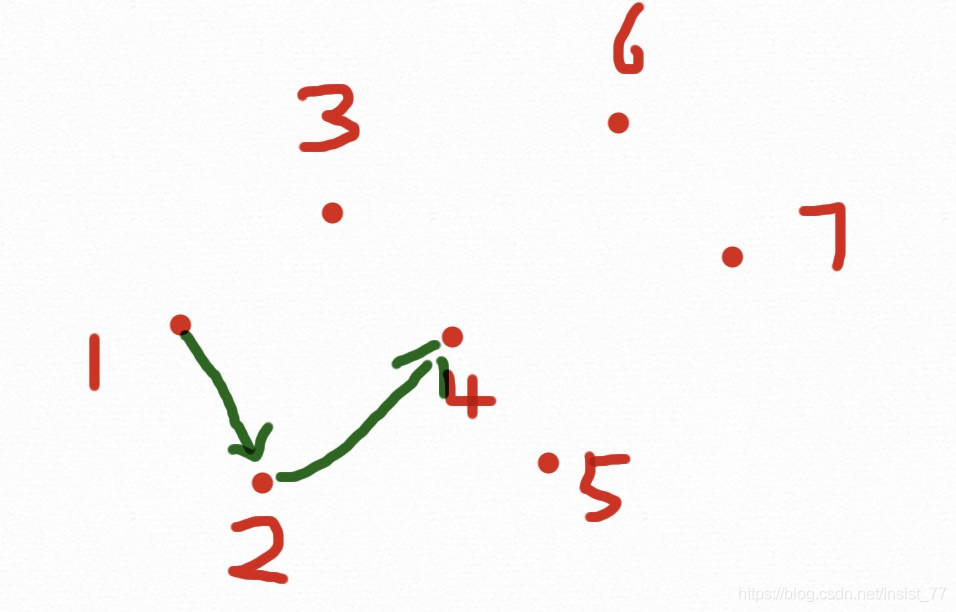
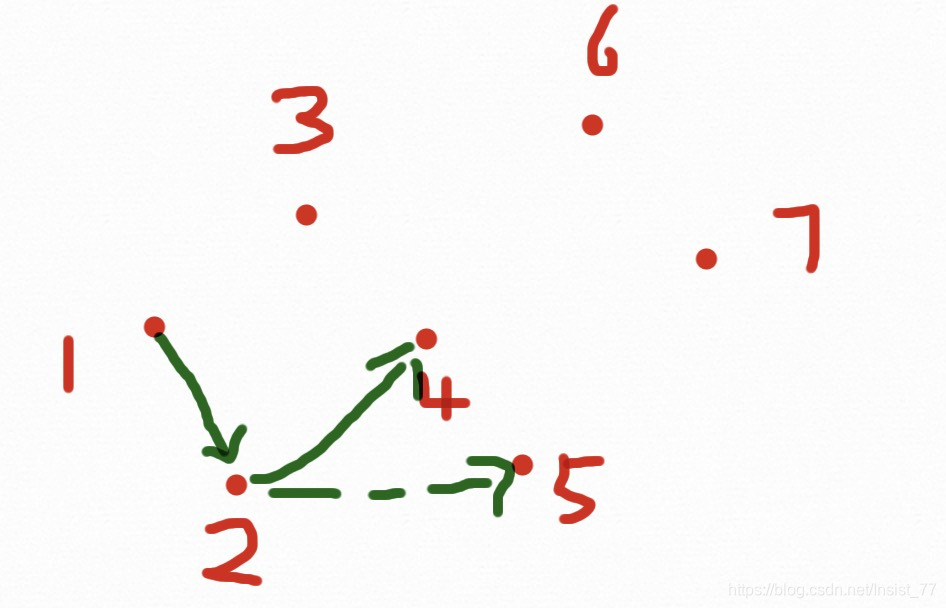
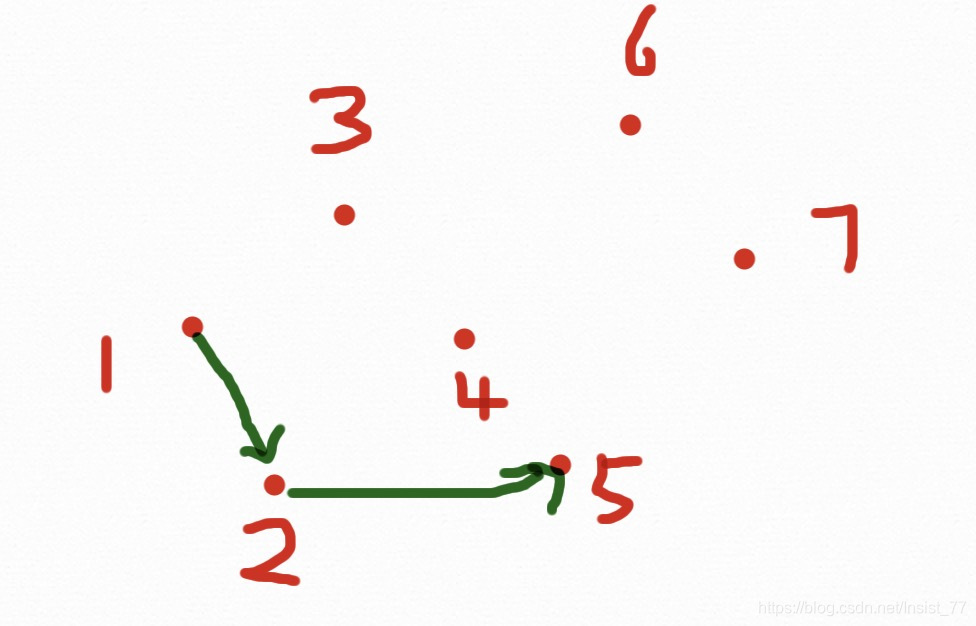
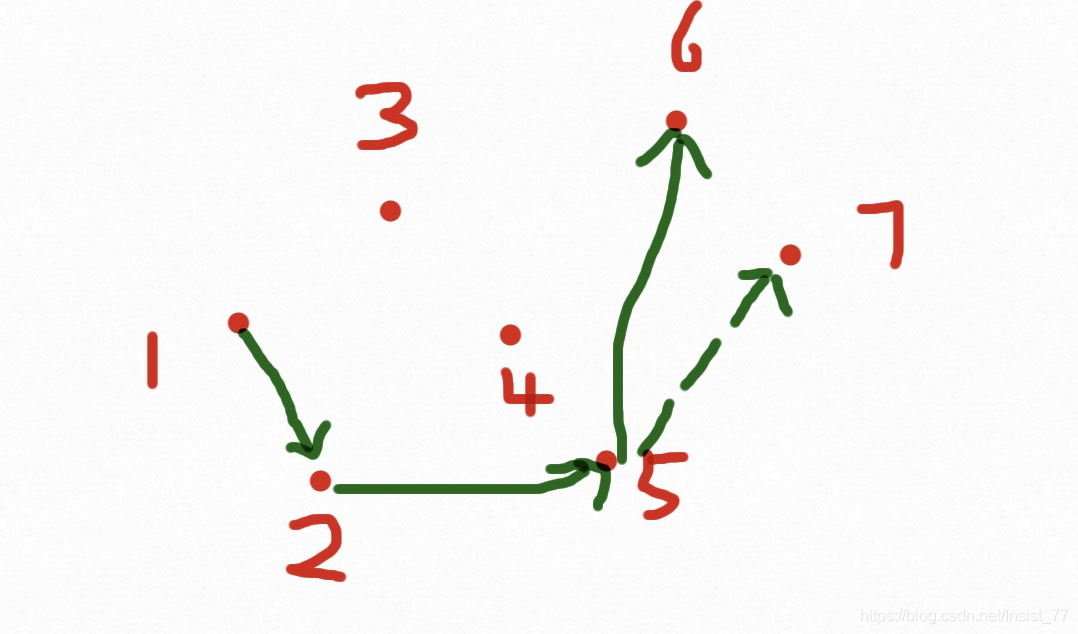
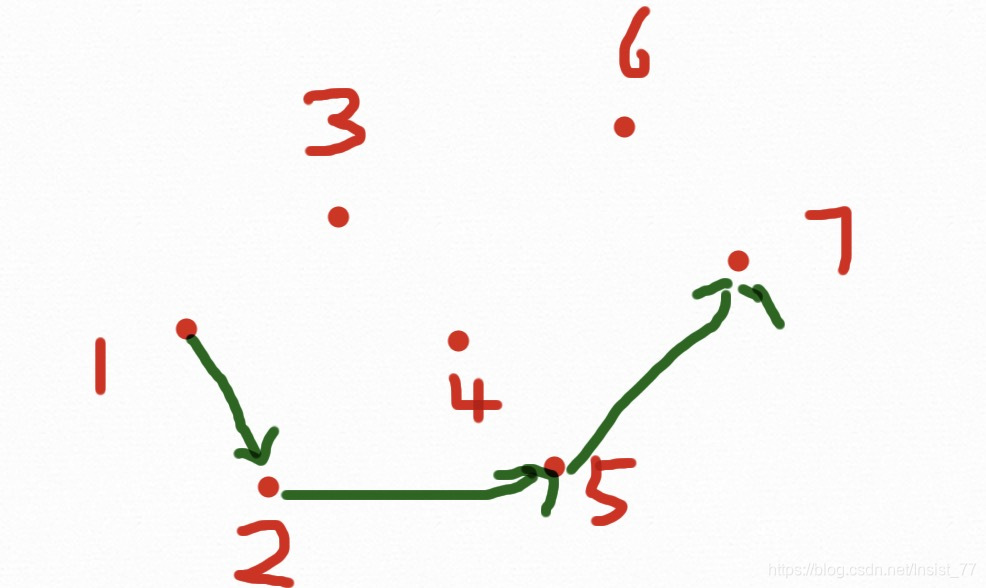
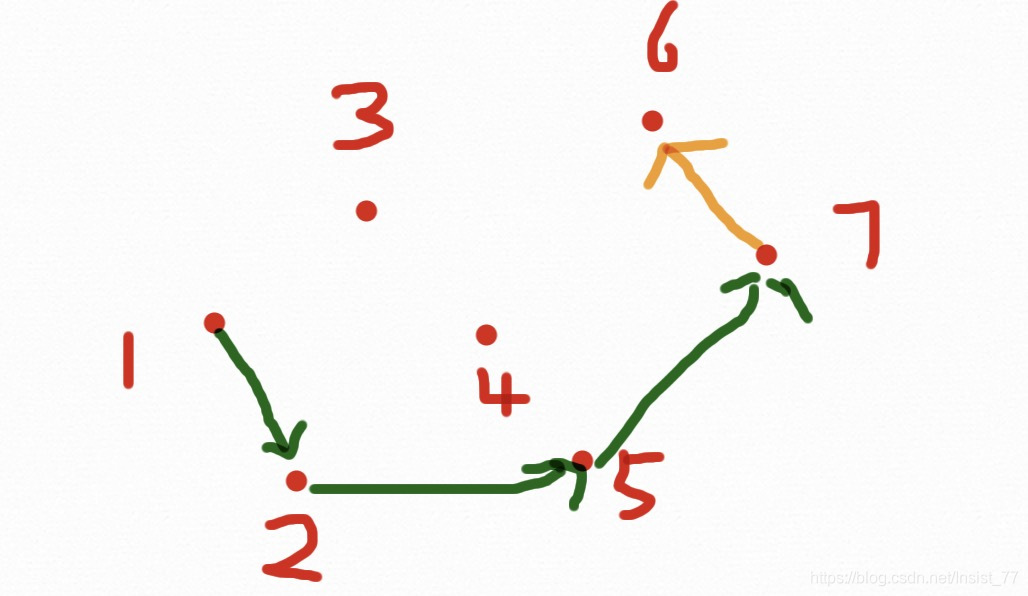
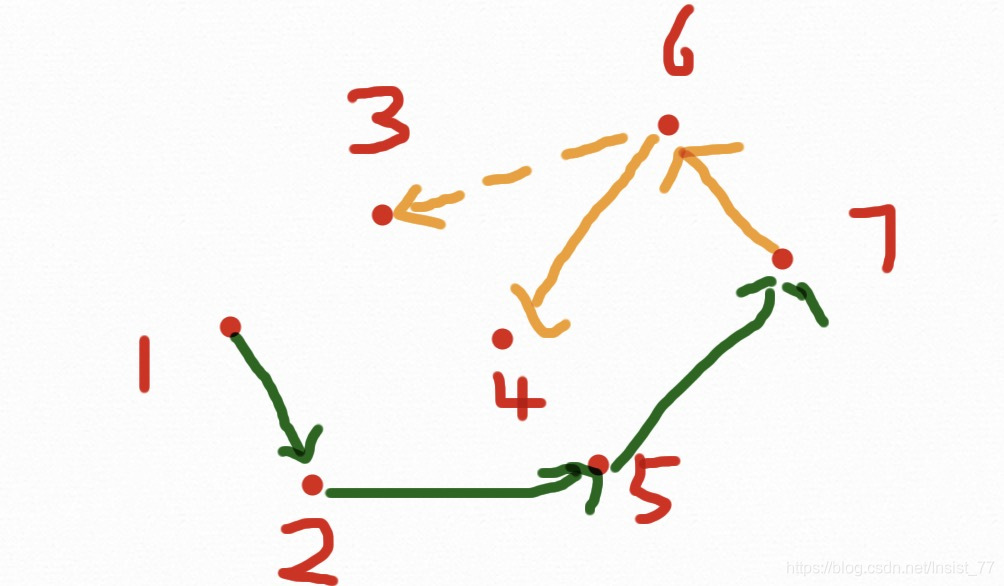
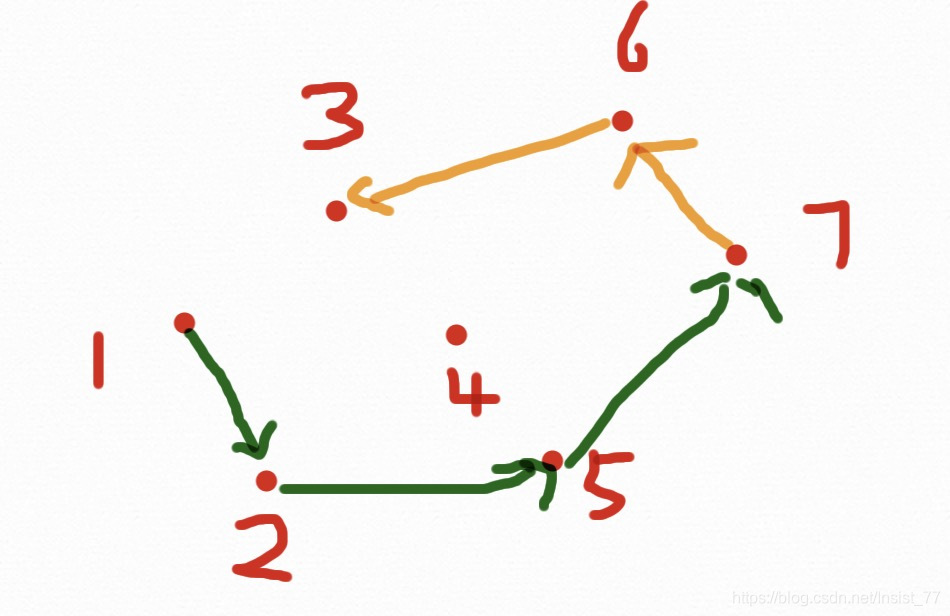
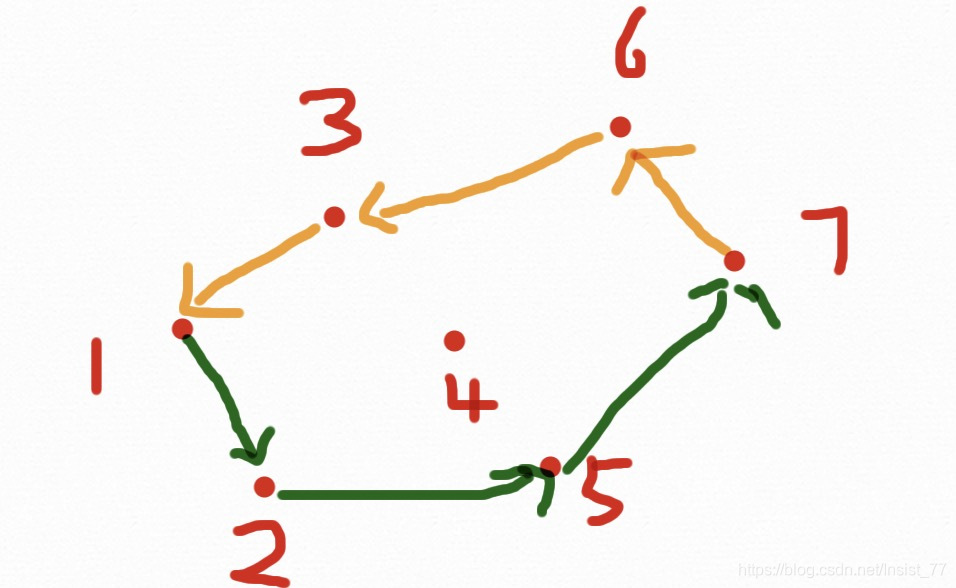
一个7个点的凸包求解过程结束，为什么会有两种颜色的线呢？因为我们事先把点排好了顺序，使得前进过程一直向右，这样的话只能求出下凸包，为了求解上凸包，我们需要从Pn-2往左求解一个上凸包，过程与下凸相同，两个相加就是凸包了。

代码：

int ConvexHull(int n,Point *ch){
    sort(p, p+n);
    int m = 0;
    for(int i=0;i<n;i++){
        while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
        ch[m++] = p[i];
    }
    
    int k = m;
    for(int i=n-2;i>=0;i--){
        while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
        ch[m++] = p[i];
    }
    if(n>1) m--;
    return m;
}

题目 UVA - 10625 完整代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
#include <vector>
#include <queue>
#include <set>
#define FRER() freopen("in.txt","r",stdin)
#define FREW() freopen("out.txt","w",stdout)
#define go int T;cin>>T;for(int kase=0;kase<T;kase++)
#define debug cout<<"****************"<<endl
#define lowbit(x) x&(-x)
#define eps 1e-6
#define mod 1000000007
using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<int,int> pii;
const int maxn = 3000 + 7;
const double PI = acos(-1);
int dcmp(double x){if(fabs(x)<eps) return 0;else return x < 0 ? -1 : 1;}
struct Point{
    double x,y;
    Point(double _x=0,double _y=0):x(_x),y(_y){}
    bool operator < (const Point& rhs) const{
        return x == rhs.x ? y < rhs.y : x < rhs.x;
    }
}p[maxn],ch[maxn];
typedef Point Vector;
Vector operator + (Vector A,Vector B){return Vector(A.x+B.x,A.y+B.y);}
Vector operator - (Vector A,Vector B){return Vector(A.x-B.x,A.y-B.y);}
bool operator == (const Point& a,const Point& b){return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;}
double Cross(Vector A,Vector B){return A.x*B.y - A.y*B.x;}//叉积
Vector Rotate(Vector A,double rad){//向量A绕起点逆时针旋转rad度
    return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
double ConvexPolygonArea(Point *p,int n){
    double area = 0;
    for(int i=1;i<n-1;i++)
        area += Cross(p[i]-p[0],p[i+1]-p[0]);
    return area/2;
}
double torad(double an){
    return an/360*2*PI;
}
int ConvexHull(int n,Point *ch){
    sort(p, p+n);
    int m = 0;
    for(int i=0;i<n;i++){
        while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
        ch[m++] = p[i];
    }
    
    int k = m;
    for(int i=n-2;i>=0;i--){
        while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--;
        ch[m++] = p[i];
    }
    if(n>1) m--;
    return m;
}
int main(){
    //FRER();
    //FREW();
    int n,tot;
    go{
        tot = 0;
        double area = 0;
        scanf("%d",&n);
        for(int i=0;i<n;i++){
            double x,y,w,h,j,ang;
            scanf("%lf%lf%lf%lf%lf",&x,&y,&w,&h,&j);
            Point o(x,y);
            ang = -torad(j);
            p[tot++] = o + Rotate(Vector(-w/2,-h/2), ang);
            p[tot++] = o + Rotate(Vector(w/2,-h/2), ang) ;
            p[tot++] = o + Rotate(Vector(-w/2,h/2), ang) ;
            p[tot++] = o + Rotate(Vector(w/2,h/2), ang)  ;
            area += w*h;
        }
        int m = ConvexHull(tot,ch);
        printf("%.1f %%\n",area*100/ConvexPolygonArea(ch, m));
    }
}