数据科学 7 线性回归
主要内容:
- 线性回归的模型、目标与算法
- 正则化方法
- 岭回归、 LASSO算法、弹性网络
- 算法汇总
- 最小二乘法、极大似然估计、正则化的最小二乘法
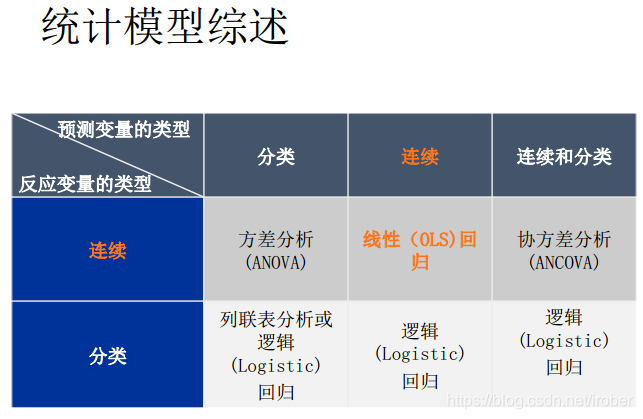
7.1 相关性分析
7.1.1 概念
1、相关关系
- Negative
- Positive
- Zero
2、Pearson 相关系数

7.2 线性回归
7.2.1 简单线性回归
目标:
- 评估预测变量在解释反应变量的变异或表现时的显著性。
- 在给定预测变量值的情况下预测反应变量值。
1、单变量的线性回归

2、简单线性回归模型

3、简单线性回归的估计

4、模型评价-拟合优度

5、模型假设检验
原假设:
- 简单线性回归模型并不比基线模型好
- β 1 = 0 \beta1=0 β1=0
备选假设:
- 简单线性回归模型确实拟合得比基线模型好。
- β 1 ≠ 0 \beta1 \not= 0 β1=0
7.2.2 多元线性回归
1、两变量的多元线性回归

2、多元线性回归模型

7.2.3 多元线性回归的变量筛选
1、自变量进入方式
多元线性回归在选择自变量进入模型的方式时,有以下几种技术:
• 向前法:逐次增加变量,进行F检验和T检验,计算残差平方和,判断加入的变量对因变量是否有显著影响。
• 向后法:所有变量进入模型,然后逐次减少变量,判断减少的变量对因变量是否有显著影响。
• 逐步法
决策的指标可为偏回归平方和、 AIC/BIC、 R方等。

7.3 线性回归的诊断
7.3.1 多元线性回归的假设
1.Y的平均值能够准确地被由X组成的线性函数建模出来。
2.解释变量和随机扰动项不存在线性关系。(建模人员解决)
3.解释变量之间不存在线性关系(或强相关)。 (建模人员解决)
4.假设随机误差项
ε
\varepsilon
ε是一个均值为0的正态分布。
5.假设随机误差项
ε
\varepsilon
ε的方差恒为
σ
2
\sigma^2
σ2 。
6.误差是独立的。
1、线性:因变量与自变量间的线性关系:
• 模型参数和被解释变量之间是线性关系。
y
y
y =
β
0
\beta_0
β0 +
β
1
x
2
+
u
\beta_1x^2 + u
β1x2+u
y
y
y =
β
0
\beta_0
β0 +
β
1
l
n
(
x
)
+
u
\beta_1ln(x) + u
β1ln(x)+u
y
y
y =
e
(
β
0
e^(\beta_0
e(β0 +
β
1
x
+
u
)
\beta_1x + u)
β1x+u)
l
n
(
P
/
(
1
−
P
)
)
ln(P/(1-P))
ln(P/(1−P)) =
β
0
\beta_0
β0 +
β
x
+
u
\beta x + u
βx+u (其中P为Y=1的概率)
- 解释变量和被解释变量之间可以是任意关系,可以在回归前进行任意函数变换。
2、假定正交:误差项与自变量不相关, 其期望为0
- E(ux)=0,即扰动项和解释变量不能线性相关。
- 该假设提示我们在建立模型时,只要同时和x,y相关的变量就应该纳入到模型中,否则回归系数就是有偏的。
- 该条假设是不能在回归后根据结果进行检验(通过工具变量法进行内生性检验并不总有效,这是计量经济学的前沿问题)。最小二法本身就是正交变换,即使该假设不被满足,任何估计的方法产生的残差都会和解释变量正交。
3、独立同分布:残差间相互独立,且遵循同一分布,要求方差齐性。
c o v ( u ) = [ a . . . c ⋮ ⋱ ⋮ d ⋯ f ] cov(u) = \left[ \begin{matrix} a & ... & c\\ \vdots & \ddots & \vdots \\ d & \cdots & f \\ \end{matrix} \right] cov(u)=⎣⎢⎡a⋮d...⋱⋯c⋮f⎦⎥⎤
4、正态性:残差服从正态分布。

7.3.2 残差分析
目标:
- 复习线性回归的假设
- 用散点图和残差图对假设进行检查。
- 分别观察以下情况:
- 残差中是否有离群值?
- 残差散点图是否和某个解释变量有曲线关系?
- 残差的离散程度是否和某个解释变量有关?
1、查看残差图

2、解决办法
1)、 X和Y为非线性关系:加入X的高阶形式,一般加X2已经足够了;
2)、异方差:横截面数据经常表现出异方差现象(比如“信用卡支出分析”数据),修正的方法有很多,比如加权最小二乘法、稳健回归,但是最简单的方法是对Y取自然数;
3)、自相关:分析时间序列和空间数据时经常遇到这个现象,复杂的方法是使用时间序列或空间计量方法分析,简单的方法是加入Y的一阶滞后项进行回归。
7.3.3 强影响点分析
举例:
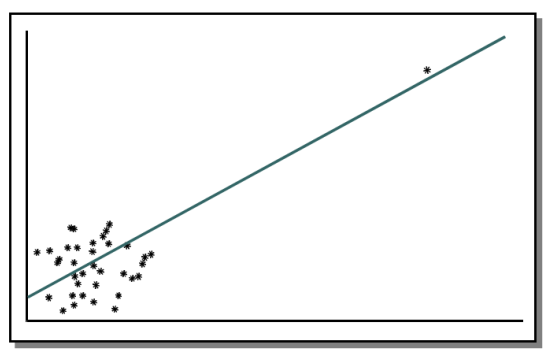
1、学生化残差
- 学生化残差=残差/标准误差
- 强影响点的识别:
- |SR| > 2 为相对小的影响点
- |SR| > 3 为相对大的影响点
2、解决强影响点的对模型的负作用
1)、查看数据本身,确定强影响点的观测是否存在错误.
2)、如果数据本身没有问题,应考虑使用其他模型对数据进行分析.
3)、 将强影响点删除,再进行分析.
• 高阶回归模型可能可以解决线性回归的对异常值表现不佳的问题,例如多项式回
归或交互项回归.
7.3.4 多重共线性分析
1、多重共线性诊断
线性回归提供以下工具去诊断与量化自变量的多重共线性问题:
- 方差膨胀因子
V I i = 1 1 − R i 2 VI_i = \dfrac{1}{1-R_i^2} VIi=1−Ri21- 方差膨胀因子> 10 表示某变量的多重共线性严重.
- 特征根与条件指数
- 无截距的多重共线性分析
2、一个有效的线性模型流程

3、回到线性回归的模型假设
1)、 模型设置, 选择何种回归方法、 如何选变量、 变量以何种形式放入模型(根据理论、 看散点图) ;
2)、 解释变量和扰动项不能相关(根据理论或常识判断,无法检验);
3)、 解释变量之间不能强线性相关(膨胀系数) ;
4)、 扰动项独立同分布; (异方差检验、 DW检验)
5)、 扰动项服从正态分布 (QQ检验)
- 3-5检验只能保证模型精确, 1、 2保证模型是正确的 。
- 违反假设1,则模型预测能力差;
违反假设2,则回归系数估计有偏;
违反假设3,则回归系数的标准误被放大;
违反假设4,则扰动项的标准差估计不准,
T检验失效;
违反假设5,则T检验失效。
- 违反假设1,则模型预测能力差;
结论: 统计方法只能帮我们做精确的模型,不能帮我们做正确的模型。
7.4、数值预测评估原理
模型建立后,要经过检验才能判定其是否合理,通过检验的模型才能用来作预测
1)、预测误差 e
e
=
x
−
x
′
e = x-x'
e=x−x′ 相对误差检验法
2)、百分误差 PE
P
E
=
e
x
∗
100
%
=
x
−
x
′
x
∗
100
%
PE = \dfrac{e}{x} * 100\% = \dfrac{x-x'}{x}*100\%
PE=xe∗100%=xx−x′∗100%
r
e
l
(
i
)
rel(i)
rel(i)=(
y
i
y_i
yi-
y
i
^
\hat{y_i}
yi^)/
y
i
y_i
yi
3)、平均误差 ME
M
E
=
e
‾
=
1
n
∑
i
=
1
n
e
i
=
1
n
∑
i
=
1
n
(
x
−
x
′
)
ME = \overline{e} = \dfrac{1}{n}\sum\limits_{i=1}^ne_i= \dfrac{1}{n}\sum\limits_{i=1}^n(x-x')
ME=e=n1i=1∑nei=n1i=1∑n(x−x′) 计算平均相对误差得
4)、平均绝对误差 MAE
M
A
E
=
∣
e
‾
∣
=
1
n
∑
∣
e
∣
=
1
n
∑
∣
x
−
x
′
∣
MAE=|\overline{e}|=\dfrac{1}{n}\sum|e|=\dfrac{1}{n}\sum|x-x'|
MAE=∣e∣=n1∑∣e∣=n1∑∣x−x′∣
5)、平均绝对百分对误差 MAPE
M
A
P
E
=
1
n
∑
∣
P
E
∣
=
1
n
∑
∣
(
x
−
x
′
)
∣
x
∗
100
%
MAPE = \dfrac{1}{n}\sum|PE|=\dfrac{1}{n}\sum\dfrac{|(x-x')|}{x}*100\%
MAPE=n1∑∣PE∣=n1∑x∣(x−x′)∣∗100%
6)、均方差 MSE
M
S
E
=
∑
e
2
n
−
1
=
(
x
−
x
′
)
2
n
−
1
MSE = \dfrac{\sum e^2}{n-1}=\dfrac{(x-x')^2}{n-1}
MSE=n−1∑e2=n−1(x−x′)2
7)、误差标准差 SDE
S
D
E
=
∑
e
2
/
(
n
−
1
)
SDE = \sqrt{\sum e^2/(n-1)}
SDE=∑e2/(n−1)
7.5 正则化方法
遇到共线性问题的解决办法:
1)、提前筛选变量。在回归之前通过决策树、随机森林、相关检验或变量聚类的方法事先解决变量高度相关的问题。因为决策树是贪婪算法,理论上也只是在大部分情况下起效,不过简单易用。
2)、子集选择 这是传统的方法,包括逐步回归和最优子集法等,对可能的部分子集拟合线性模型,利用判别准则 (如AIC,BIC,Cp,调整R2 等)决定最优的模型。因为该方法是贪婪算法,理论上这种方法只是在大部分情况下起效,实际中需要与方法1相结合。
3)、收缩方法(shrinkage method) 收缩方法又称为正则化(regularization)。主要是岭回归(ridge regression)和lasso回归。通过对最小二乘估计加入罚约束,使某些系数的估计为0。 其中lasso回归可以实现筛选变量的功能。
4)、维数缩减 主成分回归(PCR)和偏最小二乘回归(PLS)的方法。把p个预测变量投影到m维空间(m<p),利用投影得到的不相关的组合建立线性模型。这种方法的模型可解释性差,不常使用。
7.51 岭回归
1962年由Heer首先提出, 1970年后他与肯纳德合作进一步发展了该方法。当自变量间存在复共线性时,|X′X|≈0,我们设想给X′X加上一个正常数矩阵kI,(k>0),那么X′X+kI接近奇异的程度就会比X′X接近奇异的程度小得多。
岭回归做为β的估计应比最小二乘估计稳定,当k=0时的岭回归估计就是普通的最小二乘估计。
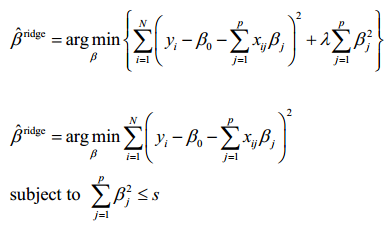


选择lambda值,使到
(1)各回归系数的岭估计基本稳定;
(2)用最小二乘估计时符号不合理的回归系数,其岭估计的符号
变得合理;
(3)交叉验证法。对lambda的各点值,进行交叉验证,选取交叉
验证误差最小的lambda值。最后,按照得到的lambda值,用全部数
据重新拟合模型即可。
7.5.2 LASSO算法
Tibshirani(1996)提出了一个新的方法来处理变量选择的问题。该方法在模型系数绝对值的和小于某常数的条件下,谋求残差平方和最小。该方法既提供了如子集选择方法那样的可以解释的模型,也具有岭回归那样的稳定性。 它不删除变量,但使得一些回归系数收缩、变小,甚至为0。因而,该方法被称为lasso(least absolute shrinkage and selection operator,最小绝对值收缩和选择算子。


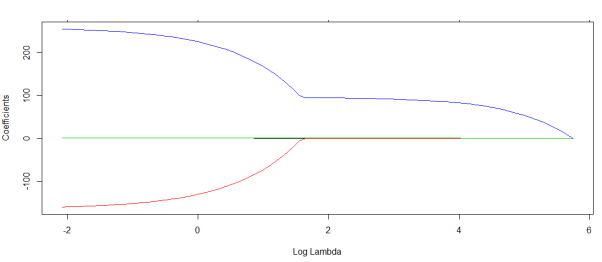
7.5.3 两者比较与弹性网络
实际上,岭回归和lasso方法都是用于处理模型变量共线性的方式。在传统线性回归当中,变量共线性极有可能导致估计的回归系数的不稳定(这一特性在样本总量较少而变量总数较多的情形下尤其显著),这一缺点可以通过对回归系数加以约束得到改善。
不妨设约束函数为如下形式,则岭回归和lasso回归可以在参数族的形式下得到统一(岭回归:r=2; lasso: r=1)
P
(
β
)
r
=
∑
j
=
1
P
∣
β
j
∣
r
≤
t
P(\beta)_r = \sum\limits_{j=1}^P|\beta_j|^r\leq t
P(β)r=j=1∑P∣βj∣r≤t
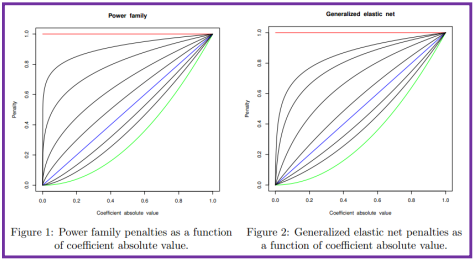
虽然只是参数取法上的不一致,但由于约束函数凹凸函数不同的特性(r<1为凹函数, r>1为凸函数)导致了最终系数特点的不一致。对于岭回归,随着t的减小,模型系数绝对值一般“步调一致”的收缩;对于lasso回归,则更倾向于将部分变量的系数收敛到0而保持另外一些变量系数的大小来达到约束条件(这实际上增加了最终系数的差异)
对于r取值的其他情形而导致的后果也可由函数凹凸性作相似推断。具体参见 Fast Sparse
Regression and Classification Jerome H. Friedman 2008


弹性网
这一参数族中r的选取也带来很多问题,对于r>1,最终系数不易收缩到0,这不助于变量的筛选;而对于r<1,随着t的减小(可以一一对应到拉格朗日方法中的λ)其系数变化呈现不连续的特征,这一问题可以通过加入“弹性系数”的方式(Generalized elastic net)得以改进(在
一定的参数取值条件下)。
λ ∑ j = 1 p ( α β j 2 + ( 1 − α ) ∣ β j ∣ ) \lambda\sum\limits_{j=1}^p(\alpha\beta_j^2+(1-\alpha)|\beta_j|) λj=1∑p(αβj2+(1−α)∣βj∣)





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










