对棋盘完美覆盖问题证明过程的质疑及其解决(续)

在上一次证明一个关于棋盘完美覆盖的问题时遗留了另一个问题没有解决。这个遗留的问题来自于一个没有被采用的证明方法。该方法的证明步骤中需要一个证明，该证明就是如果某一个棋盘完美覆盖存在同色相连的格子那么通过有限次的翻转方块就可以消除棋盘中所有的同色相连的格子。为了便于区别，这次用于覆盖棋盘的方块是由红色和绿色组成的,方块还是1乘2的矩形。所谓同色相连的格子就是指棋盘被覆盖后红色或者绿色的格子相邻。如下图所示就是一个例子：

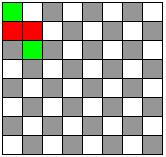
首先我们采用这样一种方法来翻转方块,就是水平放置的方块就水平翻转，这样左边的格子到右边,右边的格子到左边；垂直放置的方块就垂直翻转，这样上边的格子到下边，下边的格子到上边。对于某一个存在同色相连格子的完美覆盖，先任意选择相连格子中的一个方块，然后翻转，这样当前的这个同色相连的方格就消除了。然后看方块翻转以后是否引起新的同色相连。如果有那就继续翻转（当前翻转过的就不要再翻转了，而是翻转没有被翻转过并且是同色相连的那个方块），重复执行这个操作。如果某次翻转后没有新的同色相连的格子增加，那么就停止翻转，然后寻找棋盘中的其他同色相连的格子重复上述的过程。如果这整个过程可以顺利完成那么需要证明的问题就解决了。所以这里假设这个过程是不可能完成的，也就是说不能通过有限次翻转方块来消除所有的同色相连的格子。下面的证明就从这个假设开始，使用反证法推出矛盾从而证明原命题是成立的。

通过上述的分析可以看出，如果无法通过翻转方块消除同色相连的格子，那么在某次执行翻转的时候必定会出现这样一种情况：每次翻转一个方块在消除一个同色相连方格的同时必定会产生一个新的同色相连的格子，从而导致翻转的过程无法停止，永远继续下去，现在就要证明这是不可能的。我们假设这样的翻转执行了33次（大于32的次数都可以）。显然覆盖整个棋盘需要的方块是32个，而翻转执行了33次，那么根据鸽鸟巢原理必定存在两个方块是一样的。把这样一个被翻转的方块的序列描述如下：

K，K+1，K+2，... K+N，K

现在我们取第K个方块到第K+N个方块的序列。将这些方块首尾相连就得到一个连续的方格序列。显然这个序列中的第一个方格（方块K的第一个格子）和最后一个方格（方块K+N的第二个格子）在棋盘上是相邻的，并且这个序列中的任意2个相邻的格子在实际的棋盘中也是相邻的。这个特点是由翻转方块的方法决定的。那么在这个序列中，最初的同色相连的格子也在其中并且相邻，不失一般性假设相连的是红色格子。现在先从这个序列中拿走这两个同色相邻的红色格子，然后依次每次从这个序列中拿走两个相邻的格子，直至拿走序列中全部的格子。那么在这个过程中必定会有一次拿走的是两个绿色的格子。

这个很容易证明。首先方块的个数是整数，所以绿色方格和红色方格的总数是相同的。那么在第一次拿走两个红色格子后，后续没有一次同时拿走两个绿色格子的话，红色格子的总数和绿色格子的总数就不相等了。基于同样的理由，实际上这个结论很容易推广到更一般的情况，那就是绿色格子相连的个数和红色格子的相连个数是相等的。

由于一个方块只包含一个红色和一个绿色的格子，因此这两个绿色格子来自于两个不同的方块。可以假设这两个方块是J和J+1。好了现在我们就可以从第一个方块开始依次翻转每一个方块了。当翻转到第J个方块时，可以发现原来相邻的两个绿色格子不相邻了。因为翻转后第K个方块覆盖的绿色格子变成了红色格子。这就意味着在翻转第J个方块后没有产生新的同色相连的格子，从而导致没有必要翻转第J+1个方块，翻转的过程在这里就可以停止了。这个事实和我们的假设是矛盾的，所以原命题就得到了证明。