时间复杂度
一、时间复杂度的中n的取值范围
在1秒内的运行时限, 设计的算法复杂度为百万级别,即不能超过一千万。
即若算法的时间复杂度是O(n^2),则该n(往往在题目中会给出数据范围)不应大于3000,否则将会达到我们所说的千万数量级复杂度,从而程序运行时间超出题目中给出的用时限定。
举例来说,我们不能在1秒时限的题目当中对10000个整数进行冒泡排序,而必须使用快速排序等时间复杂度为O(nlogn)的排序算法,否则程序很可能将会得到运行时间超出限制的评判结果。
可以算出1秒内各常见时间复杂度的范围n的大小:
| 时间复杂度 | n的范围 |
| 2^n | 23 |
| n^3 | 200 |
| n^2 | 3000 |
| nlogn | 50万 |
1天 = 24hr * 60min * 60sec = 25*4000sec =10^5 sec
1生 = 1世纪 = 100yr * 365 = 3^10^4day =3*10^9 sec
"三生三世" = 300yr =10^10 sec
二、时间复杂度的分析
复杂度分析的主要方法:
1.迭代:级数求和;
2.递归:递归跟踪+递推方程
3.猜测+验证
1.级数
<1>算数级数:与末项平方同阶
T(n) = 1+2+3+ ... +n = n(n+1)/2 = O(n^2)
例1:求下段代码的时间复杂度
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
operation(i,j);
}
}基本操作operation(i,j)的运算次数为:
T(n) = n+n+...+n = n*n = O(n^2)
例2:
for(int i=0;i<n;i++) {
for(int j=0;j<i;j++) {
operation(i,j);
}
}基本操作operation(i,j)的运算次数为:
T(n) = 0+1+...+n-1 = n(n-1)/2 = O(n^2)
<2>幂方级数:比幂次高出一阶:
由:
T1(n) = 1^2+2^2+3^2+ ... +n^2 = n(n+1)(2n+1)/6 = O(n^3)
T2(n) = 1^3+2^3+3^3+ ... +n^3 = n^2(n+1)^2/4 = O(n^4)
...
<3>几何级数:与末项同阶
由:Ta(n) = a^0+a^1+...+a^n = (a^(n+1)-1)/(a-1) = O(a^n)
T(n) = 1+2+4+...+2^n = 2^(n+1)-1= O(2(n+1)) = O(2^n)
例1:
for(int i=1;i<n;i*=2)
for(int j=0;j<i;j++)
operation(i,j);T(n) = 1+2+4+2^i = 2^i-1 = O(n) (其中 2^i = n)
2.递归
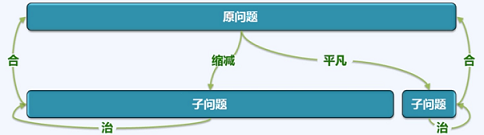
递归的算法策略:减而治之
为求解一个大规模的问题,可以将其划分为两个子问题:其一平凡,别一规模缩减
分别求解子问题,由子问题的解,得到原问题的解。
<1>递归跟踪
例:
sum(int A[], int n) {
return (n<1) ? 0 : sum(A,n-1)+A[n-1];
}递归跟踪分析:
检查每个递归实例,累计所需时间(调用语句本身,计入对应的子实例),其总和时间即为算法执行时间。
每个递归实例:0 :sum(A,n-1)+A[n-1];
左边:0 - 时间复试度 O(1)
右边:sum(A,n-1)+A[n-1] - 时间复试度也是O(1),原因:
其中:A[n-1]为O(1)
sum(A,n-1)直接忽略掉,由上面的分析,调用语句本身,计入对应的子实例。
即不记入本次的操作,它已经在子实例中被计算了。
所以,由上图总共有n次递归调用,每次为O(1),则时间复杂度为:
T(n) = 1+1+ ... +1 = O(n)
总结:递归跟踪直观形象,但仅适用于简明的递归模式。
<2>递推方程
上例中:
从递推的角度看,为求解sum(A, n),需
递归求解规模为n-1的问题sum(A, n-1) // T(n-1)
再加上A[n-1] // O(1)
递归基:sum(A,0) // O(1)
得到递推方程:T(n) = T(n-1) + O(1),T(0) = O(1)
求解:
T(n) - n = T(n-1) - (n-1) = ...
= T(2) - 2
= T(1) - 1
= T(0)
T(n) = O(1) + n = O(n)
例2:数组倒置
void reverse(int *A, int lo, int hi) {
if(lo < hi) {
swap(A[lo], A[hi]); // O(1)
reverse(A, lo + 1, hi - 1); // 忽略
}
else return; // 递归基
}
3.分而治之
为求解一个大规模的问题,可以
将其划分为若干(通常两个)子问题,规模大体相当
分别求解子问题,由子问题的解,得到原问题的解。
例1:数组求和:二分递归
sum(int A[], int lo, int hi) {
if(lo == hi) return A[lo];
int mi = (lo + hi) >> 1;
return sum(A, lo, mid) + sum(A, mid + 1, hi);
}从递推的角度看,为求解sum(A, lo, hi),需
递归求解sum(A, lo, mi)和sum(A, mi + 1, hi) // 2*T(n/2)
进而将子问题的解累加 // O(1)
递归基:sum(A, lo, lo) // O(1)
递推关系:T(n) = 2*T(n/2) + O(1)
T(n) + c = 2*(T(n/2) + c) = 2^2*(T(n/4) + c1)
= ...
= 2^(logn) * (T(1) + c1) = n*(c2 + c1)
即:T(n) = (c1 + c2)n - c1 = O(n)








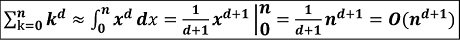















 362
362

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








