深圳大学算法导论实验二分治法求最近点对问题

一．实验目的

1. 掌握分治法思想。

2. 学会最近点对问题求解方法。

• 实验内容

1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出是N点中具有最短距离的两点。

2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。

3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。

4. 分别对N=100,1000,10000,100000，统计算法运行时间，比较理论效率与实测效率的差异，同时对蛮力法和分治法的算法效率进行分析和比较。

5. 如果能将算法执行过程利用图形界面输出，可获加分。

• 实验步骤与结果

1. 问题描述

给定平面上n个点，找到其中的一对点，使得在n个点的所有点对中，该点对的距离最小。

1. 算法原理描述

利用分治法求最近点对，将时间复杂度降为nlogn（重点是均匀平分的时间复杂度）。

2.1 新建Point结构（包含x，y信息），随机生成规模为N的点集，根据输入点集Points中的x轴进行归并排序。

2.2 当点集的点数较少时的情形

2.2.1 只有三个点 -> 返回三点之间的最小距离

2.2.2 只有两个点 -> 直接返回两点间的距离

2.2.3 只有一个点 -> 返回无穷大（DBL_MAX）

2.3 将平面点集按x排好序（归并排序），再将平面点集分割成为大小大致相等的两个数组left和right，选取点集的中位数作为垂直平分线L作为分割直线。  

1. 1. 两个递归调用，分别求出left和right中的最短距离为d1和d2。

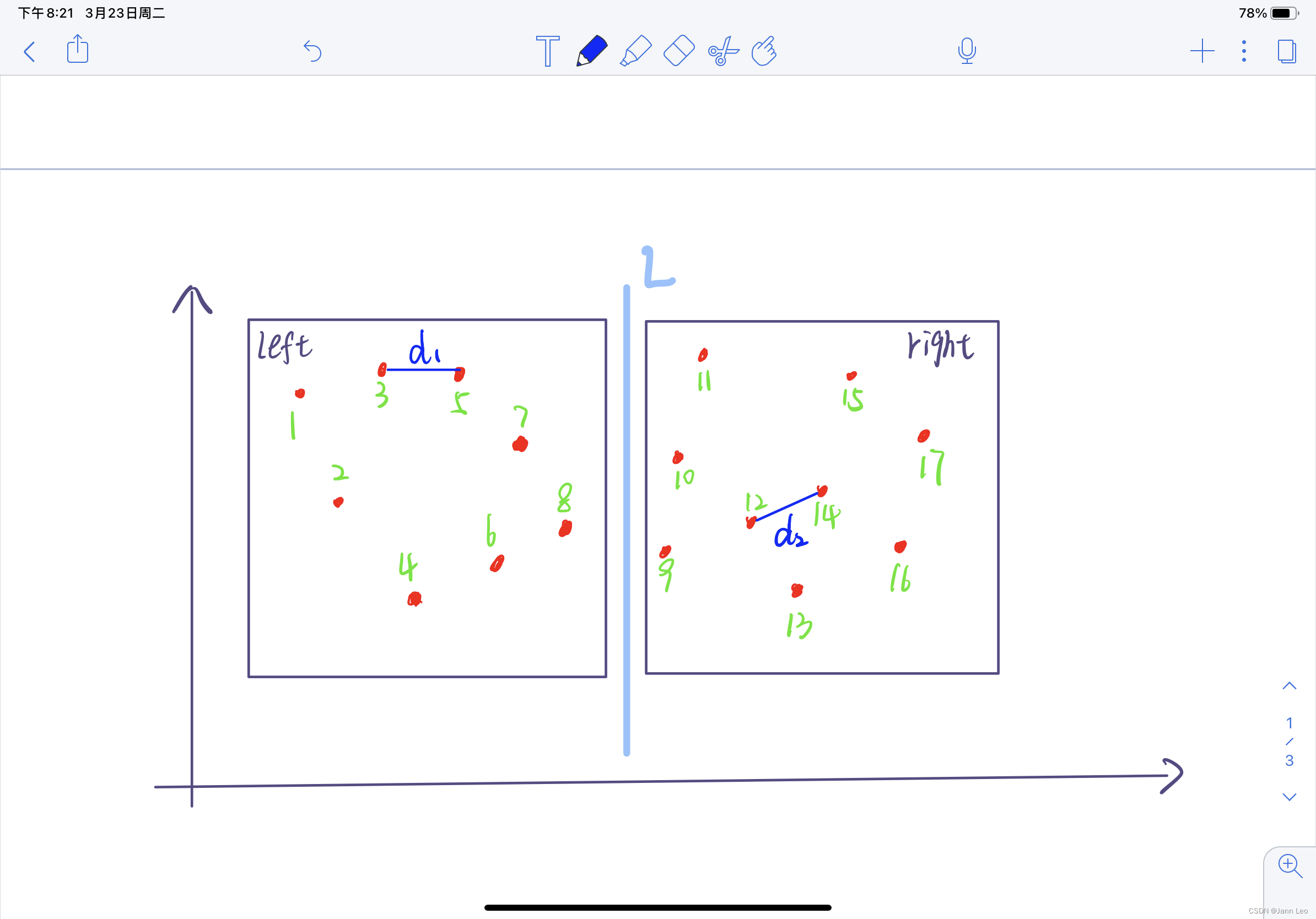
2.5 取d=min(dl, dr)，在直线L两边分别扩展d，得到边界区域Y，将点集Points按Y轴排序，S是区域Y中的点按照y坐标值排序后得到的点集，S又可分为左右两个集合s_left和s_right。

2.6因为抽屉原理，所以根据要求，当中间点距离大于分治法算出左右侧的最小距离时，p上下最多只有六个点距离等于d，所以对于中间区域中的每一点，检查它与包围它的六个点的距离，更新所获得的最近距离。

3. 算法实现的核心伪代码

预处理：先定义全局变量点集p，定义十万-一百万点集p，再生成随机点集放入栈中，最后将Points点集按x进行排序（使用合并排序）

double Min_Dis(Points[], left, right)

if(right - left ==1) 返回两点间的距离

if(right - left == 2) 返回三点间的最短距离

if (right == left)  返回无穷大

int mid = ( right + left)/2

mid_x = Points[mid].x                           // 以中位数作垂直线L

dis_left = Min_Dis(Points,left,mid)      //两次递归求出左右区间最短距离

dis_right = Min_Dis(Points,mid+1,right)

mid_dis = (dis_left <dis_right)  ? dis_left : dis_right  // 取d=min(d1, d2)

Merge_Sort(Points, left, right, cmp_y) //将点集Points[]按y轴排列 

double temp

Point *s =new Point[100000] //Point s数组存放中间区域的点

for i=left to right

if(abs(Points[i].x - mid_x)<=sqrt(min_dis))

取出符合条件的点放入s数组

for i=0 to s.lenght

j=i-3,k=i+3     //j到i表示点下方的三个点，i到k表示点上方的三个点

if j<0 j=0

if k>s.lenght k=s.lenght

for j to k && j!=i

计算点i-3 到 i+3的距离，若比min_dis更小，则更新min_dis

delete[] s

return min_dis

1. 算法测试结果及其效率分析

实验结果输出图（部分）如图4.1所示：

图4.1 实验结果图（有修改）

分别以N=100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000 为基准对各种算法进行测试。得到的运行时间表如下：

表4.1蛮力法与理论值比较（ms）

N\ms	蛮力法	理论值
100000	57630	57630
200000	223469	230520
300000	459912	518670
400000	870744	922080
500000	1430950	1440750
600000	2008390	2074680
700000	2494000	2823870
800000	3412170	3688320
900000	4462610	4668030
1000000	5220790	5763000

       表4.2分治法与理论值比较（ms）

N\ms	分治法	理论值
100000	827	827
200000	1853	1753.92
300000	2573	2718.274
400000	3861	3707.04
500000	4838	4713.961
600000	6302	5735.347
700000	7228	6768.765
800000	7801	7812.481
900000	9212	8865.201
1000000	11448	9925.921

表4.3 各算法运行时间表(ms)

N\ms	分治法	蛮力法
100000	827	48903
200000	1853	223469
300000	2573	459912
400000	3861	870744
500000	4838	1430950
600000	6953	2008390
700000	7228	2494000
800000	7801	3412170
900000	9212	4462610
1000000	11448	5220790

图4.2 蛮力法与理论值比较

图4.3 分治法与理论值比较

由表4.3可做出效率曲线图如下：

图4.4 效率曲线图

分析：

从以上的数据可以得出，在相对较大的数下，分治法对于蛮力法有明显优势，因为其时间复杂度并没有达到O(n^2)，只是达到了O(n*logn)。

综上可知，当数据规模较大时，使用分治法具有很大的优势。

思考：

1. 能否优化6个点至更少的点？

经过我查阅网上各个资源，最后发现对于我这种其实只做到了f(n)=6n,而Preparata与Shamos在1985年就提出，可以将中间点区域折半，遍历左侧点，然后在右侧d*2d的矩形中遍历6个点，也能实现最近点对查找，此时f(n)=6*(2/n),然后我又发现周玉林、熊滕荣、朱洪在1998年的论文“求平面点集最近点对的一个改进算法”中，进一步又花了Preparata与Shamos的算法，只用找四个点即可，此时f(n)为4*(2/n).

1. 为何不用随机数储存进文件，再读取？

    我有尝试过这种想法，但是在实现的时候发现，读取随机数也是一个十分耗费时间的过程，于是将其临时生成。

1. 如何生成100万个随机点集？

    将定义的对象点集数列定义为全局变量，此时就可以存放100万个点集，因为其是存放在堆中而不是栈中，因此可以实现。

四．实验心得

通过本次实验，加深了我对分治算法的认识，同时也学习了最近点对的求解方法，也明白了堆与栈的区别，也了解了随机数的生成与存放随机数的方法，分析了蛮力法与分治法求最近点对的时间复杂度，熟悉了主定理法求时间复杂度。

同时，在进行算法设计中，若控制数据读写、修改的操作尽量减少，对于算法性能提升也具有一定效果，合理分析和利用算法能极大的提高效率。