压缩感知测量矩阵之spark常数

题目：压缩感知测量矩阵之spark常数

        除了有限等距性质RIP之外，Spark常数也是经常使用的一个评价传感矩阵的指标。文献[1]中明确提到：

        在文献[2]更是以spark常数来恒量一个矩阵是否可以成为测量矩阵。

一、Spark常数的定义

        以上是文献[2]对spark常数的定义，将其中的式(3)和式(4)表达成一句话就是“矩阵线性相关向量组的最小数目”，其实以上及其原文中的很多公式大部分来自截图中所引的“[12]”（详见参考文献[3]）。

        以上文献[2] 的截图提到的“文献[4]”（详见参考文献[4]）中对spark的原定义为

二、Spark常数意义

        在以上文献[2]的截图中最后提到：当且仅当spark(Φ)>2k时，可以通过最小0范数优化问题得到k-稀疏信号x的精确近似。

        这个实际上是唯一影射问题，可简单证明如下：

        若spark(Φ)>2k，则对于任意2k稀疏信号θ有Φθ≠0（这一点不明白的话那就找本线性代数去看线性相关的定义）；又因为任意2k稀疏信号θ可以分解为两个k稀疏信号，例如：

θ=[0,0,1,2,3,4,0,0]=[0,0,1,2,0,0,0,0]－[0,0,0,0,－3,－4,0,0]= θ_k1－θ_k2

所以Φ(θ_k1－θ_k2)≠0，即Φθ_k1≠Φθ_k2，也就是说两上k稀疏信号经过压缩观测后不会映射到同一个观测向量。

        这个在文献[5]中专门以定理形式给出：

三、Spark常数与矩阵的秩

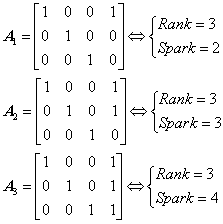
        在以上文献[4]的截图中提到：如果矩阵A没有全零列，那么spark(A)≥2；虽然spark与秩(rank)在某些方面很相似，但它们实际上是完全不同的，矩阵的秩是最大的线性无关的列数，而Spark是最小的线性相关的列数；有的时候矩阵满秩但spark=2。这个有点儿绕，看了文献[6]中的下图之后就明白了：

        以下再给出几个矩阵：

四、结语

        Spark并没有RIP那么常见，就这么大概了解一个概念吧。Spark应该与RIP有什么联系吧，RIP中也提到了2K列不相关，即Spark>2K，慢慢以后再说吧。

        另外就是Spark其实也是针对传感矩阵的，但还是如RIP中所说，在测量矩阵与稀疏矩阵满足某种不相关关系时就等价到了测量矩阵吧，木有严格证明，看到了再说吧。

        不知道大家有没有一个感觉：越学压缩感知越感觉自己是小白，为啥看啥啥不懂呢？

 

参考文献：

【1】焦李成，杨淑媛，刘芳，侯彪. 压缩感知回顾与展望[J].电子学报，2011，39(7)：1651-1662.

【2】党骙，马林华，田雨，张海威，茹乐，李小蓓. m序列压缩感知测量矩阵构造[J]. 西安电子科技大学（自然科学版），2015，42(2)：215-222.

【3】Shu-Tao Xia, Xin-Ji Liu, Yong Jiang, Hai-TaoZheng. Deterministic Constructions of Binary Measurement Matrices from FiniteGeometry[OL]. http://arxiv.org/pdf/1301.5952v2.pdf

【4】D.L. Donoho, M. Elad, Optimally sparserepresentation in general (nonorthogonal) dictionaries vial1 minimization[J]. Proc. Nat. Acad. Sci., 2003,100(5): 2197-2202.

【5】王法松，张林让，周宇. 压缩感知的多重测量向量模型与算法分析[J]. 信号处理，2012，28(6)：785-792.

【6】HuoChengfu. 稀疏表示(Sparse Representation)_Elad' slide，新浪博客