题目:二次规划问题和MATLAB函数quadprog的使用
二次规划(Quadratic Programming,QP)问题的一般形式为:
其中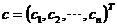
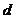
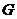
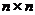
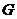
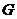
对于非凸规划,由于存在比较多的驻点,求解比较困难。
根据约束条件的不同,二次规划可分为等式约束二次规划问题和不等式约束二次规划问题。等式约束二次规划问题即只含有等式约束,常见的解法有直接消去法、广义消去法、拉格朗日(Lagrange)法;对于不等式约束二次规划问题,其基本思想是把不等式约束转化为等式约束再求解,常见解法有有效集(active set)方法,有效集方法在每步迭代中把有效约束作为等式约束,然后可以用拉格朗日法求解,重复直到求得最优解。
很多学者专门研究各类二次规划的求解方法,如文献[4][5],对于非数学专业的的人来讲更重要的是怎么把二次规划当作一个工具去使用它。
在MATLAB中求解二次规划的的函数是quadprog,具体使用方法可查询帮助文件。

【例】求如下二次规划问题。
【分析】首先应该把目标函数表示成如下矩阵形式:
这里要细说一下如何写成矩阵形式。
首先,向量x是很容易写出的,因为f(x)包含两个变量x1和x2,因此
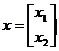
其次,向量f只与两个变量x1和x2的一次项有关,所以fTx=-2x1-6x2,因此
最后,矩阵H只与两个变量x1和x2的二次项有关,所以
本例中,
目标函数搞定之后,下面来看约束条件部分,约束条件应该写成如下形式:
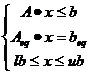
本例中约束条件只有不等式约束,因此Aeq和beq为空,对于A和b很容易就可以得出来:
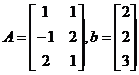
而约束条件中对变量x1和x2只给出下限,没有给上限,因此ub为空,
得到了所有的参数,将参数输入MATLAB,编程如下:(代码是直接在Command Window中一行一行录入的,所以每行前面有符号“>>”)
>> H = [1 -1; -1 2];
>> f = [-2; -6];
>> A = [1 1; -1 2; 2 1];
>> b = [2; 2; 3];
>> lb = [0; 0];
>> [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb)Warning: Large-scale algorithm does not currently solve this problem formulation,
using medium-scale algorithm instead.
> In quadprog at 291
Optimization terminated.
x =
0.6667
1.3333
fval =
-8.2222
exitflag =
1
output =
iterations: 3
constrviolation: 0
algorithm: 'medium-scale: active-set'
firstorderopt: []
cgiterations: []
message: 'Optimization terminated.'
lambda =
lower: [2x1 double]
upper: [2x1 double]
eqlin: [0x1 double]
ineqlin: [3x1 double]【1】孙文瑜, 徐成贤,朱德通.最优化方法(第二版)[M]. 北京:高等教育出版社, 2010.
【2】龚纯,王正林. 精通MATLAB最优化计算[M].北京: 电子工业出版社,2009.
【3】lnsunqingshen, 464518439.什么是凸二次规划, 百度知道,2011-06-20.
【4】李明强.几类特殊凸二次规划问题的求解算法研究[D].山东科技大学,2013 .
【5】于绍慧.边界约束凸二次规划的求解[D].南京航空航天大学,2005.








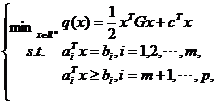
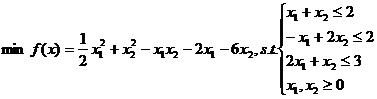
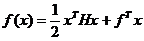
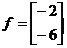
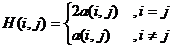
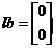
















 2046
2046

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








