一:装载问题
有一批共n个集装箱要装上2艘载重量分别为c1和c2的船,其中集装箱i的重量为wi,且
装载问题要求确定是否有一个合理的装载方案可将这些集装箱装上这2艘船。如果有,找出一种装载方案。
例如当n=3,c1=c2=50且w=[10,40,40]时,则可以将集装箱1和2装到第一艘轮船上,而将集装箱3装到第二艘轮船上;如果w=[20,40,40],则无法将这3个集装箱都装上轮船。
分析:
容易证明,如果一个给定装载问题有解,则首先将第一艘船尽可能装满再将剩余的集装箱装上第二艘船可得到最优装载方案。将第一艘船尽可能装满等价于选取全体集装箱的一个子集,使该子集中集装箱重量之和最接近c1。用回溯法解装载问题, 时间复杂度O(2^n),在某些情况下优于动态规划算法。
剪枝方案是如果当前已经选择的全部物品载重量cw + 剩余集装箱的重量r<= 当前已知的最优载重量bestw,则删去该分支。
回溯法实现
#include<iostream>
using namespace std;
int n;//集装箱数
int w[40];//集装箱重量
int c1,c2;//两艘船的载重量
int ans;//当前载重量
int bestans;//当前最优载重量
int r;//剩余集装箱重量
void backtrack(int i) {
tal++;
if(i>n) {
if(ans>bestans) {
bestans=ans;
}
return;
}
r-=w[i];
if(ans+w[i]<=c1) {
ans+=w[i];
backtrack(i+1);
//改回辅助的全局变量
ans-=w[i];
}
//剪枝函数,当前已装的重量和剩下的重量 小于 最优重量,则不必往下递归了
if(ans+r>bestans) backtrack(i+1);
//改回辅助的全局变量
r+=w[i];
}
int main() {
cin>>n>>c1>>c2;
int i=1;
int sum=0;
//集装箱总重量
while(i<=n) {
cin>>w[i];
r+=w[i];
sum+=w[i];
i++;
}
backtrack(1);
backtrack(1);
if(bestans>0&&((sum-bestans)<=c2)) {
cout << "轮船1装载的重量为:" <<bestans << "轮船2装载的重量为:"<< sum-bestans << endl;
} else if(sum<=c2) cout<<bestans<<endl;
else cout<<"No"<<endl;
}假如题目改为:要给出所有可实现装载的排列,则可以枚举实现
#include<iostream>
#include<algorithm>
using namespace std;
int n;//集装箱数
int w[40];//集装箱重量
int c1,c2;//两艘船的载重量
int ans;//当前载重量
int bestans;//当前最优载重量
int r;//剩余集装箱重量
int A[100];//用于放置当前序列
int bestA[100];//用于放置最优序列
int vis[100];//用于记录哪些节点以被访问
int tal = 0;
void back(int cur) {
tal++;
if(cur > n) { //走到了边界
if(ans > bestans) {
bestans = ans;
for(int i = 1; i <= n; i++) {
bestA[i] = A[i];
}
}
} else {
for(int i = 1; i <= n; i++) {
if(!vis[i] && ans + w[i] <= c1 && ans+r > bestans) { //剪枝
r -= w[i];
ans += w[i];
A[cur] = w[i];
vis[i] = 1;
back(cur+1);
vis[i] = 0;
A[cur] = 0;
ans -= w[i];
r += w[i];
}
if(ans + w[i] > c1) {
back(cur+1);
}
}
}
}
int main() {
cin >> n >> c1 >> c2;
for(int i = 1; i <= n; i++) {
cin >> w[i];
r += w[i];
}
int sum = r;
ans = bestans = 0;
back(1);
bool ok = true;
if(r - bestans > c2) {
ok = false;
}
if(ok) {
cout << "轮船1可以装载以下重量的物品:";
for(int i = 1; i <= n; i++) {
if(bestA[i] != 0) {
cout << bestA[i] << " ";
}
}
cout << endl << "轮船2装载以下重量的物品:" << r-bestans;
}else{
cout << "物品过重,无法装载";
}
cout << endl << tal;
}二:最大团问题
完全子图: 给定无向图G=(V, E),U是V的子集。如果对任意u,v属于U有(u,v)属于E,则称U是G的完全子图。
团: 当且仅当U不包含在G的更大的完全子图中,G的完全子图U是G的团。
最大团: 是指G中所含顶点数最多的团。
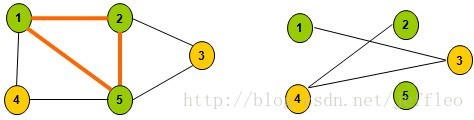
如图所示,给定无向图G={V, E},其中V={1,2,3,4,5},E={(1,2),(1,4),(1,5),(2,3),(2,5),(3,5),(4,5)}。
根据最大团定义,子集{1,2}是图G的一个大小为2的完全子图,但不是一个团,因为它包含于G的更大的完全子图{1,2,5}之中。{1,2,5}是G的一个最大团。{1,4,5}和{2,3,5}也是G的最大团。
求:实现最大团的一种实现方式
分析
剪枝策略:如果剩余未考虑的顶点数加上团中顶点数不大于当前解的顶点数,可停止回溯。用邻接矩阵表示图G,n为G的顶点数,cn存储当前团的顶点数,bestn存储最大团的顶点数。当cn+n-i < bestn时,不能找到更大的团,利用剪枝函数剪去
这个问题的关键:如何判断某个顶点是否是最大团的其中一个顶点?
由于子集的排列时从小到大的,例如{1,2,3},而不会出现{3,2,1},因此不用遍历全部顶点,遍历cur前的顶点即可,因为cur已经是子集排列的最后一位
然后从vis[i] = 1表示已选择的顶点,用当前要放入的顶点 和 已选择顶点依次结合,如果它们组成的队列彼此都有边,则说明将要放入的顶点,放入之后可以组成团;如果存在其中一个顶点和将要放入的顶点无边,则该顶点放入后,不能组成团
bool isTuan(int cur){
for(int i=1; i<cur; i++){
/*vis[i]代表第i个顶点,如果i顶点是选中的顶点,然而该顶点和cur顶点无边,说明不是最大团
例如vis[1]=1, vis[2]=1,cur=3,说明已选择了123,
然而graph[1][3]=0,无边,说明cur不是团中的一员 */
if(vis[i] && !graph[i][cur]){
return false;
}
}
return true;
}代码
#include<iostream>
using namespace std;
int v,e,graph[100][100];//v顶点数 e边数 graph图的邻接矩阵
int cn, bestn;//cn 当前团的顶点数 bestn最大团的顶点数
int corder[100], bestorder[100];//corder 当前团的顶点集 bestorder 最大团的顶点集
int vis[100];// 记录已选的顶点
//由于子集的排列时从小到大的,例如{1,2,3},而不会出现{3,2,1},因此不用遍历全部顶点
//遍历cur前的顶点即可,因为cur已经是子集排列的最后一位
bool isTuan(int cur){
for(int i=1; i<cur; i++){
/*vis[i]代表第i个顶点,如果i顶点是选中的顶点,然而该顶点和cur顶点无边,说明不是最大团
例如vis[1]=1, vis[2]=1,cur=3,说明已选择了123,
然而graph[1][3]=0,无边,说明cur不是团中的一员 */
if(vis[i] && !graph[i][cur]){
return false;
}
}
return true;
}
void backtrace(int cur){
if(cur > v){
if(cn > bestn){
bestn = cn;
for(int i=1; i<=v; i++){
if(corder[i] != 0)
cout << corder[i] << " ";
}
cout << endl;
}
}
if(isTuan(cur)){
cn++;
vis[cur] = 1;
corder[cur] = cur;
backtrace(cur+1);
cn--;
vis[cur] = 0;
corder[cur] = 0;
}
//剪枝函数,如果当前团的顶点数 + 剩余的顶点数 小于 当前以得的最大团顶点数,则剪去
if(cn + v-cur > bestn){
backtrace(cur+1);
}
}
int main(){
cin >> v >>e;
int i,j;
for(i=1; i<=v; i++){
for(j=1; j<=v; j++){
graph[i][j] = 0;
}
}
//输入边
for(int k=1; k<=e; k++){
cin >> i >> j;
graph[i][j] = 1;
}
backtrace(1);
cout << bestn << endl;
} 三、总结分析,求一个子集问题的算法框架
从上面的装载问题和最大团问题可以看出,因此两者的代码流程很相似,这是因为:
两个问题都是求实现的其中一种方案,而不是全部方案,因此不用遍历把全部方案列举出来,只要求得满足的一个方案就结束程序
求一个子集问题的算法框架:
void backtrace(int cur){
if(cur > n) {
记录best方案
}
if(满足约束条件){
backtrace(cur+1);
}
if(满足剪枝条件(当前已选 + 剩余的 > 当前已记录的最好的)){
backtrace(cur+1);
}
}








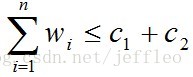














 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








