manacher 算法详解 pku 3974

manacher算法:

定义数组p[i]表示以i为中心的(包含i这个字符)回文串半径长

将字符串s从前扫到后for(int i=0;i<strlen(s);++i)来计算p[i],则最大的p[i]就是最长回文串长度,则问题是如何去求p[i]?

由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]....p[i-1]

假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义maxlen是i+k位置前所有回文串中能延伸到的最右端的位置,即maxlen=p[i]+i;//p[i]+i表示最大的

分两种情况:

1.i+k这个位置不在前面的任何回文串中,即i+k>maxlen,则初始化p[i+k]=1;//本身是回文串

然后p[i+k]左右延伸,即while(s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k]

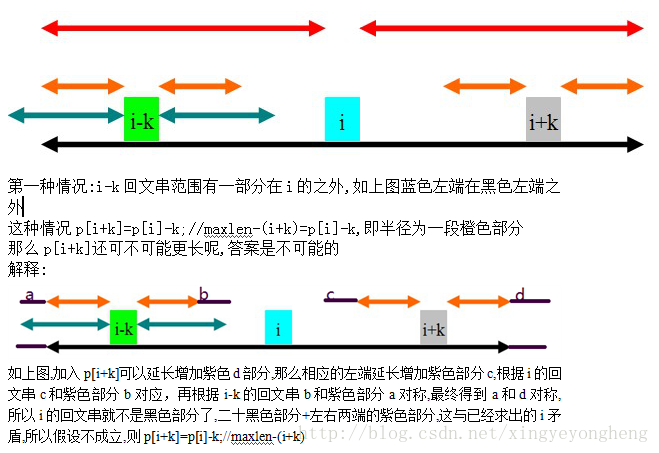
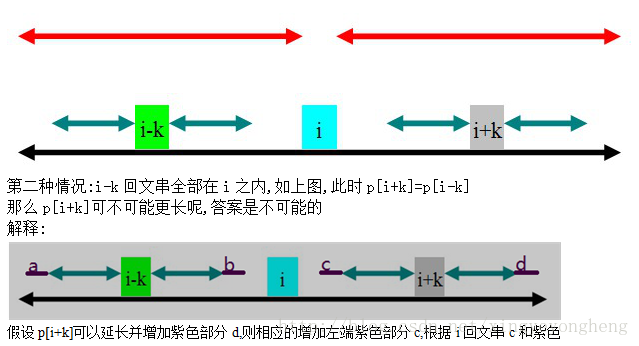
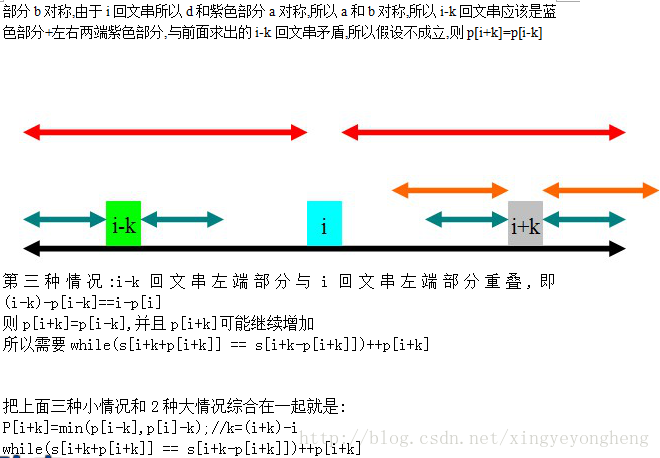
2.i+k这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k

这样的话p[i+k]就不是从1开始

由于回文串的性质,可知i+k这个位置关于i与i-k对称,

所以p[i+k]分为以下3种情况得出

//黑色是i的回文串范围,蓝色是i-k的回文串范围,

hdu3068代码:

[cpp]  view plain  copy

 print ?

1. #include<iostream>  
2. #include<cstdio>  
3. #include<cstdlib>  
4. #include<cstring>  
5. #include<string>  
6. #include<queue>  
7. #include<algorithm>  
8. #include<map>  
9. #include<iomanip>  
10. #define INF 99999999  
11. using namespace std;  
12.   
13. const int MAX=110000+10;  
14. char s[MAX*2];  
15. int p[MAX*2];  
16.   
17. int main(){  
18.     while(scanf("%s",s)!=EOF){  
19.         int len=strlen(s),id=0,maxlen=0;  
20.         for(int i=len;i>=0;--i){//插入'#'  
21.             s[i+i+2]=s[i];  
22.             s[i+i+1]='#';  
23.         }//插入了len+1个'#',最终的s长度是1~len+len+1即2*len+1,首尾s[0]和s[2*len+2]要插入不同的字符   
24.         s[0]='*';//s[0]='*',s[len+len+2]='\0',防止在while时p[i]越界  
25.         for(int i=2;i<2*len+1;++i){  
26.             if(p[id]+id>i)p[i]=min(p[2*id-i],p[id]+id-i);  
27.             else p[i]=1;  
28.             while(s[i-p[i]] == s[i+p[i]])++p[i];  
29.             if(id+p[id]<i+p[i])id=i;  
30.             if(maxlen<p[i])maxlen=p[i];  
31.         }  
32.         cout<<maxlen-1<<endl;  
33.     }  
34.     return 0;  
35. }  

这里介绍O(n)回文子串（Manacher）算法

算法基本要点：首先用一个非常巧妙的方式，将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度：在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。 为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#。

下面以字符串12212321为例，经过上一步，变成了 S[] = "$#1#2#2#1#2#3#2#1#";

然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]），比如S和P的对应关系：

S     #  1  #  2  #  2  #  1  #  2  #  3  #  2  #  1  #
P     1   2  1  2  5   2  1  4   1  2  1  6   1  2   1  2  1
(p.s. 可以看出，P[i]-1正好是原字符串中回文串的总长度）

下面计算P[i]，该算法增加两个辅助变量id和mx，其中id表示最大回文子串中心的位置，mx则为id+P[id]，也就是最大回文子串的边界。

这个算法的关键点就在这里了：如果mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i)。

具体代码如下：

if(mx > i)
{
      p[i] = (p[2*id - i] < (mx - i) ? p[2*id - i] : (mx - i));
}
else
{
       p[i] = 1;
}

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

当 P[j] > mx - i 的时候，以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能一个一个匹配了。

对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了

下面给出原文，进一步解释算法为线性的原因

 

回文串定义：“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。
回文子串，顾名思义，即字符串中满足回文性质的子串。
经常有一些题目围绕回文子串进行讨论，比如 HDOJ_3068_最长回文，求最长回文子串的长度。朴素算法是依次以每一个字符为中心向两侧进行扩展，显然这个复杂度是O(N^2)的，关于字符串的题目常用的算法有KMP、后缀数组、AC自动机，这道题目利用扩展KMP可以解答，其时间复杂度也很快O(N*logN)。但是，今天笔者介绍一个专门针对回文子串的算法，其时间复杂度为O(n)，这就是manacher算法。
大家都知道，求回文串时需要判断其奇偶性，也就是求aba和abba的算法略有差距。然而，这个算法做了一个简单的处理，很巧妙地把奇数长度回文串与偶数长度回文串统一考虑，也就是在每个相邻的字符之间插入一个分隔符，串的首尾也要加，当然这个分隔符不能再原串中出现，一般可以用‘#’或者‘$’等字符。例如：
原串：abaab
新串：#a#b#a#a#b#
这样一来，原来的奇数长度回文串还是奇数长度，偶数长度的也变成以‘#’为中心的奇数回文串了。
接下来就是算法的中心思想，用一个辅助数组P记录以每个字符为中心的最长回文半径，也就是P[i]记录以Str[i]字符为中心的最长回文串半径。P[i]最小为1，此时回文串为Str[i]本身。
我们可以对上述例子写出其P数组，如下
新串：	#	a	#	b	#	a	#	a	#	b	#
P[]  : 	1	2	1	4	1	2	5	2	1	2	1
我们可以证明P[i]-1就是以Str[i]为中心的回文串在原串当中的长度。
证明：
1、显然2*P[i]-1即为新串中以Str[i]为中心最长回文串长度。
2、以Str[i]为中心的回文串一定是以#开头和结尾的，例如“#b#b#”或“#b#a#b#”所以L减去最前或者最后的‘#’字符就是原串中长度的二倍，即原串长度为(L-1)/2，化简的P[i]-1。得证。
依次从前往后求得P数组就可以了，这里用到了DP(动态规划)的思想，也就是求P[i]的时候，前面的P[]值已经得到了，我们利用回文串的特殊性质可以进行一个大大的优化。我先把核心代码贴上：
   
   

    
    

     
     

      
      [cpp] 
      
      view plain
      
       copy
      
      

      
       
     
     
    
    
    
    
for(i=1;i<n;i++)  
{  
    if(MaxId>i)  
    {  
        p[i]=Min(p[2*id-i],MaxId-i);  
    }  
    else  
    {  
        p[i]=1;  
    }  
    while(Str[i+p[i]]==Str[i-p[i]])  
    {  
        p[i]++;  
    }  
    if(p[i]+i>MaxId)  
    {  
        MaxId=p[i]+i;  
        id=i;  
    }  
}  
   
   
为了防止求P[i]向两边扩展时可能数组越界，我们需要在数组最前面和最后面加一个特殊字符，令P[0]=‘$’最后位置默认为‘\0’不需要特殊处理。此外，我们用MaxId变量记录在求i之前的回文串中，延伸至最右端的位置，同时用id记录取这个MaxId的id值。通过下面这句话，算法避免了很多没必要的重复匹配。

   
   

    
    

     
     

      
      [cpp] 
      
      view plain
      
       copy
      
      

      
       
     
     
    
    
    
    
if(MaxId>i)  
{  
    p[i]=Min(p[2*id-i],MaxId-i);  
}  
   
   
那么这句话是怎么得来的呢，其实就是利用了回文串的对称性，如下图，
j=2*id-i即为i关于id的对称点，根据对称性，P[j]的回文串也是可以对称到i这边的,但是如果P[j]的回文串对称过来以后超过MaxId的话，超出部分就不能对称过来了，如下图，所以这里P[i]为的下限为两者中的较小者，p[i]=Min(p[2*id-i],MaxId-i)。
算法的有效比较次数为MaxId次，所以说这个算法的时间复杂度为O(n)。

这几个讲的还是比较详细了，不像某些灌水的

ac 代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
char a[2100000], b[1100000];
int p[2100000];
int main()
{
int k = 0;
while (~scanf("%s", b))
{
if (!strcmp(b, "END"))
break;
int i, len = strlen(b);
for (i = 0; i < len; i++)
{
a[(i << 1) + 2] = b[i];
a[(i << 1) + 3] = '#';
}
a[0] = '$', a[1] = '#';
len = (len << 1) + 2;
a[len] = 0;
//puts(a);
int MM = 0, id = 0, mp = 0;
for (i = 1; i < len; i++)
{
if (mp > i)
p[i] = min(mp - i, p[2 * id - i]);
else
p[i] = 1;
for (; a[i - p[i]] == a[i + p[i]]; p[i]++);
if (i + p[i] > mp)
{
mp = i + p[i];
id = i;
}
MM = max(MM, p[i]);
}
printf("Case %d: %d\n", ++k, MM - 1);
}
return 0;
}