【DP~最大子立方体】吃西瓜

  吃西瓜[matrix.pas/c/cpp]

[说明]此题中出现的所有数全为整数

[背景]SubRaY有一天得到一块西瓜,是长方体形的....

[题目描述]SubRaY发现这块西瓜长m厘米,宽n厘米,高h厘米.他发现如果把这块西瓜平均地分成m*n*h块1立方厘米的小正方体,那么每一小块都会有一个营养值(可能为负,因为西瓜是有可能坏掉的,但是绝对值不超过200).

现在SubRaY决定从这m*n*h立方厘米的西瓜中切出mm*nn*hh立方厘米的一块小西瓜(一定是立方体形,长宽高均为整数),然后吃掉它.他想知道他最多能获得多少营养值.(0<=mm<=m,0<=nn<=n,0<=hh<=h.mm,nn,hh的值由您来决定).

换句话说,我们希望从一个m*n*h的三维矩阵中,找出一个三维子矩阵,这个子矩阵的权和最大.

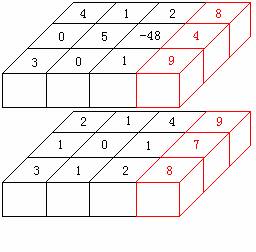
一个2*3*4的例子,最优方案为切红色2*3*1部分

[输入][matrix.in]

首行三个数h,m,n(注意顺序),分别表示西瓜的高,长,宽.

以下h部分,每部分是一个m*n的矩阵,第i部分第j行的第k个数表示西瓜第i层,第j行第k列的那块1立方厘米的小正方体的营养值.

 

[输出][matrix.out]

SubRaY所能得到的最大营养值

 

[样例输入]

2 3 4

4 1 2 8

0 5 -48 4

3 0 1 9

2 1 4 9

1 0 1 7

3 1 2 8

 

[样例输出]

45

 

[数据范围]

对于30%的数据,h=1,1<=m,n<=10

对于全部的数据,1<=h<=32,1<=m,n<=50,保证h<=m,n

 =====================================

============================

{
ID:jie19952
PROG:
LANG:PASCAL
}
var
  h,m,n:longint;
  sum,map:array[0..50,0..50,0..50]of longint;
  sum1:array[0..50,0..50]of longint;
  sum2:array[0..50]of longint;
procedure init;
begin
  assign(input,'matrix.in');
  assign(output,'matrix.out');
  reset(input); rewrite(output);
end;

procedure terminate;
begin
  close(input); close(output);
  halt;
end;

function max(a,b:longint):longint;
begin
  if a>b then exit(a);
  exit(b);
end;

procedure main;
var
  h1,m1,m2,n1,n2:longint;
  ans:longint;
begin
  readln(h,m,n);
  fillchar(map,sizeof(map),0);
  fillchar(sum,sizeof(sum),0);
  
  for h1:=1 to h do
    for m1:=1 to m do
      for n1:=1 to n do
        begin
          read(map[h1,m1,n1]);
          sum[h1,m1,n1]:=sum[h1,m1,n1-1]+map[h1,m1,n1];
        end;
        
  ans:=-maxlongint;
  For n1:=1 to n do
    for n2:=n1 to n do
      begin
        //fillchar(sum1,sizeof(sum1),0);
        for h1:=1 to h do
          begin
            sum1[h1,0]:=0;
            for m1:=1 to m do
              begin
                sum1[h1,m1]:=sum1[h1,m1-1]+sum[h1,m1,n2]-sum[h1,m1,n1-1];
              end;
          end;
        sum2[0]:=0;
        for m1:=1 to m do
          for m2:=m1 to m do
            begin
              for h1:=1 to h do
                begin
                  sum2[h1]:=max(sum2[h1-1]+sum1[h1,m2]-sum1[h1,m1-1],sum1[h1,m2]-sum1[h1,m1-1]);
                  if sum2[h1]>ans then ans:=sum2[h1];
                end;
            end;
      end;
  writeln(ans);
end;

begin
  init;
  main;
  terminate;
end.