七岁儿童的数学：图形着色，色彩数，欧拉路径和欧拉环

今天作为女儿二年级教室里的客人，教室里都是热爱数学的七八岁女孩子，我做了一个数学调查，关于图形着色、色彩数、地图着色、欧拉路径和环。我带了一大堆准备好的例图，所有的女孩们做了她们自己的图片和地图来相互挑战。最后每个孩子都编制了一个包含他们探索结果的数学“彩色书”。让我来说一说我们所做的。

 

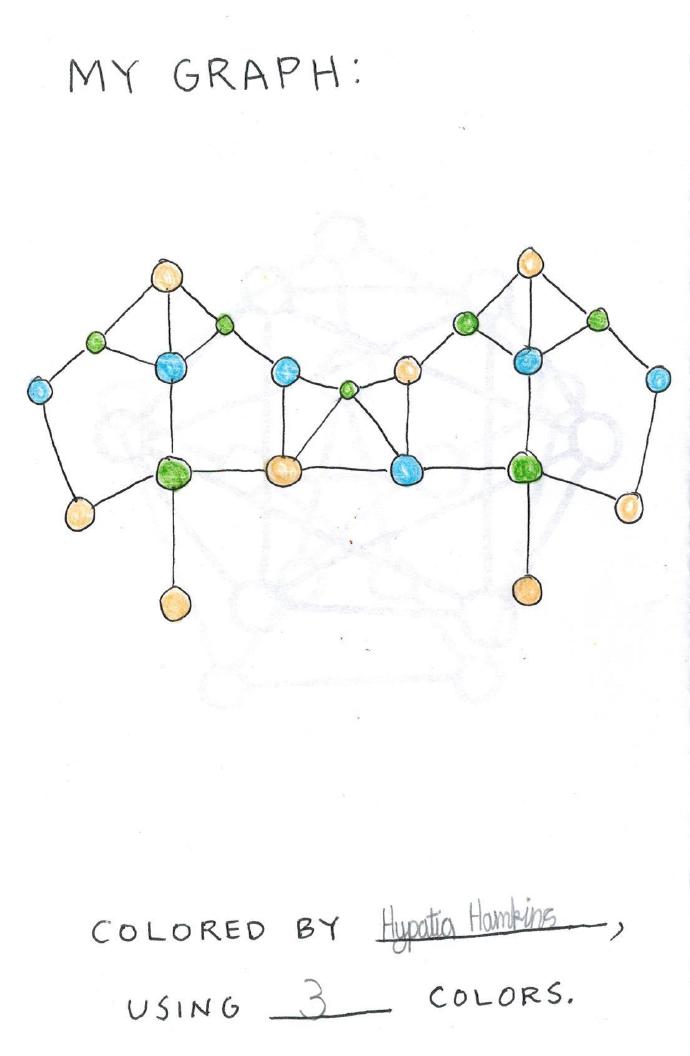
我们从顶点着色开始，给图形的每个顶点涂上不同的颜色。我们从一些简单的例子开始，然后是会让她们犯难的复杂些的图形。

 

目标是用最少的颜色种类，图形的色彩数是能够满足着色的最少颜色个数。小姑娘们给图形着色，并数出他们使用的颜色个数，我们还针对图形进行分组讨论，为什么她需要用到这些颜色。

接下来，小姑娘们两人一组，一人创作一个有挑战性的图形，由她的搭档来着色，然后互换角色。

地图着色，让地图上的每个国家有不同的颜色，当然这和图形着色是很接近的。

小姑娘们创造了他们自己的地图来相互挑战，然后着手给这些地图着色。我们讨论了这个值得注意的事实：四种颜色就能给任何地图着色。

接着，我们考虑欧拉路径和环，在这种特殊的图形中一笔即可画下所有的边，并且每条边只经过一次。我们从一些简单的例子开始，然后考虑一些复杂点的情况。

欧拉环在同一个顶点开始并结束，而欧拉路径则在一个顶点开始，在另一个顶点结束。

我们讨论了有些图形没有欧拉路径和环这一事实。如果有欧拉环，每次到达一个顶点后离开这个顶点时就会从一条新的边经过，因此每个顶点一定有偶数个边。对于欧拉路径，如果起点和终点不同，则起点和终点有奇数条边，同时其他的顶点都有偶数条边。

值得注意的是，在有限连通图中，上面的必要条件也是充分条件。这可以通过建立欧拉路径和环来证明（起点和终点是两个奇数度的节点）；每次到达一个新的顶点，就可以从另一个边离开，因此不会被卡住。如果缺少某些边（有些边没有），简单的插入合适的路线来解决，这样它会像期望的单个欧拉路径或环一样。（不过我们没有在二年级的课堂上过多的讨论这个证明。）

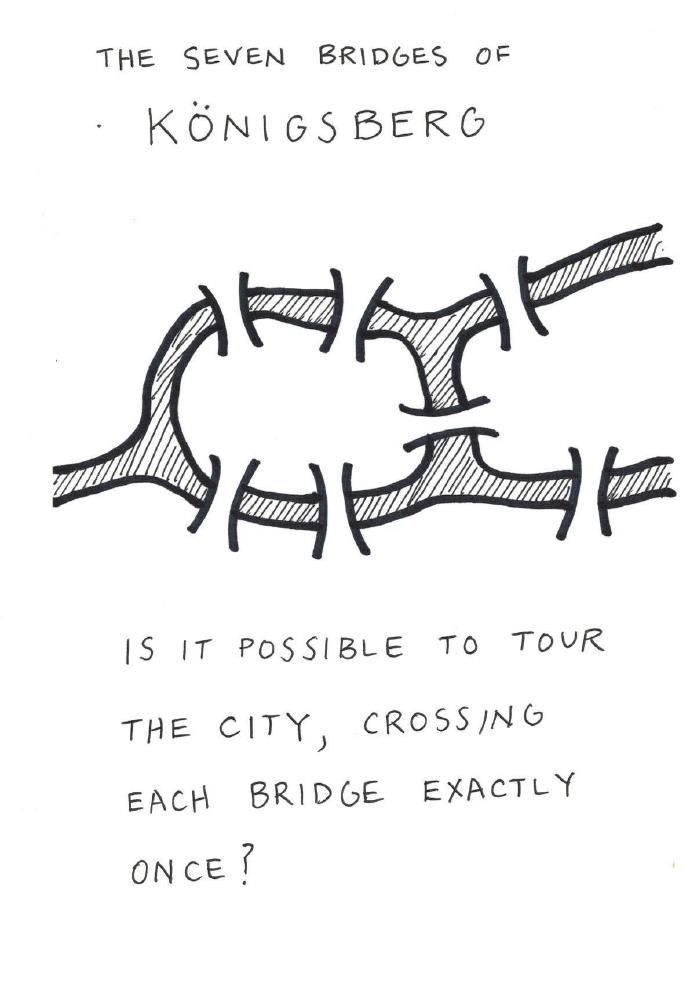
同时，这是个讨论柯尼斯堡的七座桥梁的绝好机会。能否只穿过每座桥一次就游览整个城市？

最后的收获是：一本关于有趣图形的小册子。

这一天的高潮出现在我们给图形着色的过程中，一个小姑娘走到我面前，说：“我想要成为数学家！”真让人高兴！

安德烈 鲍尔帮我作了一套没有着色的原始图形（也可以在Google+上找到），如果想制作自己的小册子这份资料就可以派上用场。把他们打印出来，两面都打印（注意正确的方向），折叠起来做成一个小册子；可以用几个回形针来装订。

可以在 MathOverflow 上看到涉及制作难以着色的地图和图形的计算难度的问题，这些是针对成年人的。

英文出处：Joel David Hamkins。