2017年伊朗国家队选拔赛第3题-CSDN博客

本文链接：https://blog.csdn.net/jinyindao243052/article/details/145468897

$I_a$ 是 $\triangle ABC$ 的 $\angle BAC$ 内的旁心. 过 $A, I_a$ 的一个圆与 $A B$ , $A C$ 的延长线分别交于点 $X$ , $Y$ . 设 $S$ , $T$ 分别是 $I_aB$ , $I_aC$ 上的点, 使得 $\angle I_aSC = \angle I_aYC$ , $\angle I_aTB = \angle I_aXB$ . $K$ 是 $BT$ 与 $CS$ 的交点, $Z$ 是 $I_aK$ 与 $ST$ 的交点. 求证: $X$ , $Z$ , $Y$ 三点共线.

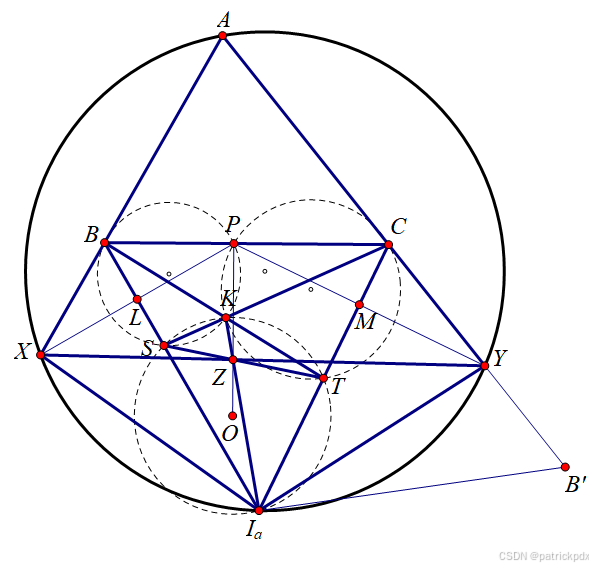
在这里插入图片描述

证明:

在这里插入图片描述

易知 $\triangle BSC \sim \triangle BXI_a$ , $\triangle CTB \sim \triangle CYI_a$ .

$\angle CKT=\angle TBC+\angle SCB=\angle BI_aX+\angle CI_aY=\frac{\pi}{2}-\frac{A}{2}$ .

$\therefore S$ , $I_a$ , $T$ , $K$ 共圆 (设圆心为 $O$ ).

作 $B$ 关于 $I_aC$ 的对称点 $B^{'}$ , 则 $BI_a=B'I_a$ , $\angle BI_aB'=\angle XI_aY=\pi-A$ , $XI_a=YI_a$ .

$\triangle BXI_a \simeq \triangle B'YI_a$ .

$BX + C Y = B^{'} Y + C Y = C B^{'} = BC$ .

在 $BC$ 上取一点 $P$ , 使得 $BP = BX$ , 则 $CP = C Y$ .

由 $\triangle CTB \sim \triangle CYI_a$ 得 $CT \cdot CI_a=CY \cdot CB=CP \cdot CB$

由 $S$ , $I_a$ , $T$ , $K$ 共圆得 $CT \cdot CI_a=CK \cdot KS$ , 所以 $B$ , $P$ , $K$ , $S$ 共圆.

类似地, 可得 $C$ , $P$ , $K$ , $T$ 共圆.

$P$ 是完全四边形 $KSI_aT$ 的密克点.

由密克点的性质, $O$ , $Z$ , $P$ 共线, 且 $Z$ 为 $P$ 关于 $\bigodot O$ 的反演点.

显然 $XP$ 被 $BI_a$ 垂直平分(交于 $L$ ), $Y P$ 被 $CI_a$ 垂直平分 (交于 $M$ ).

在这里插入图片描述

只需证 $L M$ 经过 $ZP$ 的中点 (记为 $H$ ).

过 $H$ 作 $ZP$ 的垂线 $l$ 交 $I_aS$ 于点 $L^{'}$ , 交 $I_aT$ 于 $M^{'}$ . 则 $l$ 为 $P$ 和 $\bigodot O$ 的根轴, $O$ , $S$ , $P$ , $T$ 共圆. (证明略)

$\angle L'HP=\angle L'LP=\frac{\pi}{2}$ , $L$ , $H$ , $P$ , $L^{'}$ 共圆.

$\angle M'HP=\angle M'MP=\frac{\pi}{2}$ , $M$ , $H$ , $P$ , $M^{'}$ 共圆.

由于 $l$ 是 $P$ 和 $\bigodot O$ 的根轴, $L'P^2=L'S \cdot L'I_a \Rightarrow \triangle L'PS \sim \triangle L'I_aP$ , $M'P^2=M'T \cdot M'I_a \Rightarrow \triangle M'PT \sim \triangle M'I_aP$ .