单纯形和单纯复形

最新推荐文章于 2025-01-16 18:28:21 发布

jinzhilong580231

最新推荐文章于 2025-01-16 18:28:21 发布

阅读量7.3k

点赞数 3

分类专栏：数学知识文章标签：图形 domain graph 工具

数学知识专栏收录该内容

71 篇文章

订阅专栏

转自： http://zh.wikipedia.org/wiki/%E5%8D%95%E7%BA%AF%E5%BD%A2

单纯形

几何学上，单纯形或者n-单纯形是和三角形类似的n维几何体。精确的讲，单纯形是某个n维以上的欧几里得空间中的（n+1）个仿射无关（这样的点集被称为处于一般位置）的点的集合的凸包。

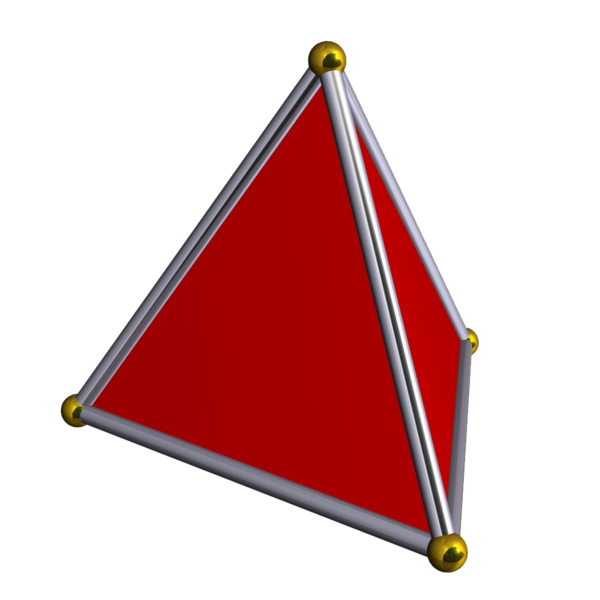
例如，0-单纯形就是点，1-单纯形就是线段，2-单纯形就是三角形，3-单纯形就是四面体，而4-单纯形是一个五胞体（每种情况都包含内部）。

正单纯形是同时也是正多胞形的单纯形。正n-单纯形可以从正(n - 1)-单纯形通过将一个新顶点用同样的边长连接到所有旧顶点构造。

我们将点看作零维空间，直线看作一维空间，平面看作二维空间

转自：http://zh.wikipedia.org/wiki/%E4%B8%80%E8%88%AC%E4%BD%8D%E7%BD%AE

一般位置

在几何学上，一些点的集的一般位置的意义是相对于某些特例的。它在不同讨论背景下有不同意义。

“一般位置”这句话最常用的意义就是点的集在d维的欧几里德空间中在一般位置，即是没有d+1点在同一个d-1维的面。例如在平面上，说点的集在一般位置，就即是没有三点共线。

在讨论平面上蒙洛诺伊空间图形或德劳内三角剖分的时候，可能会采用一个更严格的定义：点的集在一般位置，当且仅当没有三点共线且没有四点共圆。

多胞形是一类由平的边界构成的几何对象。多胞形可以存在于任意维中。多边形为二维多胞形，多面体为三维多胞形，也可以延伸到三维以上的空间，如多胞体（英语：polychoron）即为四维多胞形。

当提到n度空间下的多胞形时，常会用n-多胞形的名称来表示，因此多边形可称为2-多胞形，多面体可称为3-多胞形，多胞体即为3-多胞形。

在几何学里，胞是指一个为更高维物件的一部份之三维元素

在多胞形里

胞是为更高维多胞形的边界之一部份的三维多面体，如四维多胞形或蜂巢体(三维镶嵌)。

例如，立方蜂巢体是由立方胞所组成的，在每个边上都有四个立方体。超立方体亦是由立方胞所组成的，但一边只有三个立方体。

面是类比于胞之多面体和平面镶嵌内的二维元素。

有时，四维元素(在5-多胞形及更高维度里)会被称为“超胞”，或更易懂的“4-面”。系统化地，“n-面”为在“n+1-多胞形”或更高维内的元素。

立方蜂巢体 - 每一边有四个立方胞

   单纯形是代数拓扑中最基本的概念。
　　考虑实数域的n维向量空间 R^n, 设a_0,a_1,a_2,...,a_n是一组向量，
　　使得{a_1-a_0,a_2-a_0,...a_n-a_0}线性无关。
　　设E={p=s_0a_0+s_1a_1+s_2a_2+...+s_na_n| s_0+s_1+...s_n=1}
　　点集E就称为一个n维单纯形。
　　1维单纯形就是线段；2维单纯形就是三角形；三维单纯形就是立体三角形。
　　人们希望能够把一个拓扑对象剖分成许多个小的单纯形，要求任何两个相邻的单纯形相交的公共部分仍是一个单纯形－－这种剖分称为（曲）单纯剖分。
　　在曲面情形，就是熟知的三角剖分。
　　单纯剖分是研究代数拓扑的基本手段，由此可以构造一系列拓扑不变量，如欧拉示性数。它是研究同调论的基本工具。

单纯复形 Simplicial Complex

A simplicial complex is a set T of simplices such that
- any face of a simplex in T is a simplex in T
- two simplices in T either are disjoint or share a common sub-face.

The dimension d of a simplicial complex is the maximal dimension of its simplices.
A simplicial complex T is pure if any simplex of T is included in a simplex of T with maximal dimension.
Two simplexes in T with maximal dimension d are said to be adjacent if they share a d-1 dimensional sub-face.
A simplicial complex is connected if the adjacency relation defines a connected graph over the set of simplices
of T with maximal dimension.
The union UT of all simplices in T is called the domain of T. A point p in the domain of T is said to singular if
its surrounding in UT is neither a topological ball nor a topological disc.
　　数学中，由三角形组成的一种几何图形。通过把一般的图形和这些较简单的图形按规定方式对应起来，可以简化一般图形的拓补（定性的）研究。这些基本的三角形成为二维单纯复形，简称二维单形，更高维的单纯复形也可以用三角形的高维类似物（即通常所说的N维单行；三维单行是四面体）构成。

这些三角形必须用一定的方式，即只能在顶点或沿着它们的整个边界相合而拼接在一起。用代数方法研究给定复形的定点、边界与三角形之间的关系，可以得到刻画这些三角形在复形中的拓补排列的代数结构，从而也就刻画了这个复形所赖以构成的原来图形的拓补。