学习整理
B. Bünz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille and G. Maxwell, “Bulletproofs: Short Proofs for Confidential Transactions and More,” 2018 IEEE Symposium on Security and Privacy (SP), 2018, pp. 315-334, doi: 10.1109/SP.2018.00020.
https://ieeexplore.ieee.org/document/8418611
(除算数电路部分以外的3,4章,省略了Perfectly Binding等性质证明)
并且回顾了Jim Miller新提出的Fiat-Shamir转换的严重漏洞及对Bulletproofs的破坏:
https://blog.trailofbits.com/2022/04/13/part-1-coordinated-disclosure-of-vulnerabilities-affecting-girault-bulletproofs-and-plonk/
https://blog.trailofbits.com/2022/04/15/the-frozen-heart-vulnerability-in-bulletproofs/
关于这个漏洞原理较简单的介绍,可以先看这一篇
https://blog.csdn.net/jiongxv/article/details/124267364
Bulletproofs
改进的内积证明
内积证明要证明关系(1):
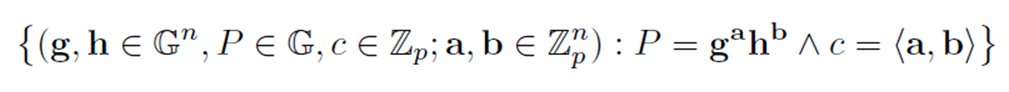
Notations

简化的范例

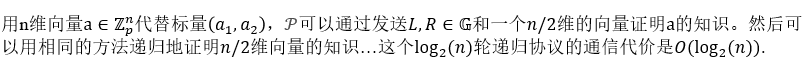
内积证明
前面的范例可以给出一个向量
a
{\rm a}
a满足关系
P
=
g
a
P={\rm g^a}
P=ga的证明(标量),改进的内积证明协议可以同时进行两个向量的证明,并证明关系(1)。
Protocol 1
(
u
u
u是相对于
g
,
h
{\rm g,h}
g,h具有未知离散对数的固定群元)
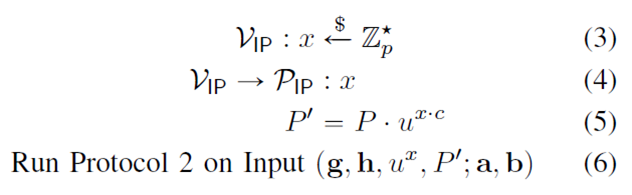
要证明的关系(1)等价变换为关系(2):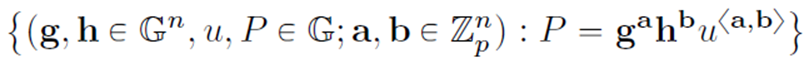
Protocol 2
注意Protocol 1对Protocol 2的调用,Protocol 2中所使用的
u
u
u其实是
u
x
u^x
ux.

n
=
1
n=1
n=1是递归算法终止的条件,此时输入的"向量"
a
,
b
a,b
a,b和群元
g
,
h
g,h
g,h都是一维的(实际上是标量)。
递归的循环部分
n
>
1
n>1
n>1,采用了一种"二分法"思路:
①②③④分别对应简化的标量实例中的相应步骤

(为了简化表示,把
[
:
n
′
]
[:n']
[:n′]表示为
l
l
l,
[
n
′
:
]
[n':]
[n′:]表示为
r
r
r,即一个向量分成的左右两半)
则每次循环计算:

所以,
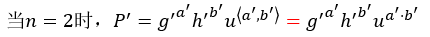
对数大小的范围证明
零知识范围证明
证明范围关系转化证明内积关系
用改进的内积证明构造一个范围证明,这个证明使验证者确信承诺
V
V
V中包含一个数字
v
v
v,它在一定范围内,而没有揭示
v
v
v:
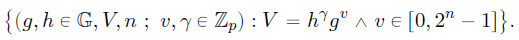
证明者:
把
v
v
v转换成包含它的位的向量
a
L
=
(
a
1
,
.
.
.
,
a
n
)
∈
{
0
,
1
}
n
{\rm a}_L=(a_1,...,a_n)\in \{0,1\}^n
aL=(a1,...,an)∈{0,1}n,有
⟨
a
L
,
2
n
⟩
=
v
\left\langle{\rm a}_L,\bm{2}^n\right\rangle=v
⟨aL,2n⟩=v; 并将
a
L
{\rm a}_L
aL委托给常数规模的承诺
A
∈
G
A\in \mathbb{G}
A∈G;
将证明
v
∈
[
0
,
2
n
−
1
]
v\in[0,2^n-1]
v∈[0,2n−1]关系转换成使验证者相信证明者知道: 承诺
A
A
A对应的向量
a
L
∈
Z
p
n
{\rm a}_L\in\mathbb{Z}_p^n
aL∈Zpn满足以下关系:
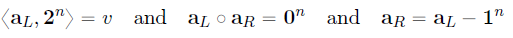
下面要将证明这
2
n
+
1
2n+1
2n+1个约束转换成证明一个内积关系,以便使用内积证明。为了做到这一点,取约束的随机线性组合(由验证者选择)。如果原始约束不满足,那么在挑战空间中,组合约束不可能成立。
-
证明委托的向量 b {\rm b} b满足 b = 0 n {\rm b}=\bm{0}^n b=0n,验证者需要向证明者发送一个随机的 y ∈ Z p y\in\mathbb{Z}_p y∈Zp,而证明者需要证明 ⟨ b , y n ⟩ = 0 \left\langle{\rm b},{\rm y}^n\right\rangle=0 ⟨b,yn⟩=0(这种情况下 b ≠ 0 n {\rm b}\neq\bm{0}^n b=0n的概率可忽略)
-
证明上面的关系又可变换为证明(这是为简化下一步组合将向量式转换为标量式):
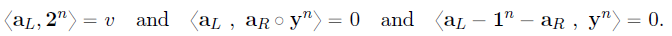
-
将三个等式合并(随机线性组合),使用一个由验证者发送的随机 y ∈ Z p y\in\mathbb{Z}_p y∈Zp,证明者证明:
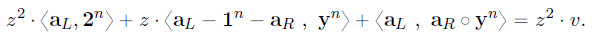
-
整理等式(合并内积,分离与 a {\rm a} a独立无关的项):
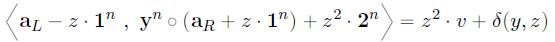
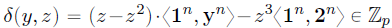
因此要证明的原关系转化为了证明单个的内积关系。如果将内积中的两个向量作为证明发送给验证者,验证者只需要用 v v v的承诺 V V V(以及他自己选择的挑战 y , z y,z y,z)即可验证关系。 -
但是,这两个向量并不是零知识的,它们揭示了 a L {\rm a}_L aL的知识,所以不能直接发送。所以引入两个盲化向量 s L , s R {\rm s}_L,{\rm s}_R sL,sR.
零知识证明协议
Setup:

构造证明:
按照上文所述原理,构造两个1次向量多项式和一个2次多项式:
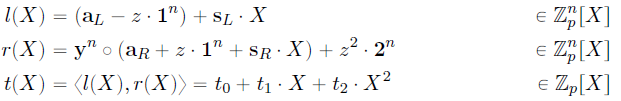
(注意:多项式内积的定义:
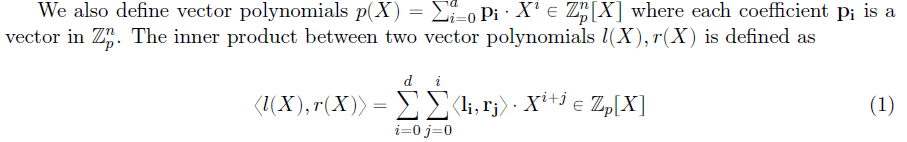
)
为了证明关系成立,证明者需要说服验证者0次系数
t
0
t_0
t0满足:
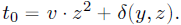
证明者还需向验证者提交其他系数(即
t
1
,
t
2
t_1,t_2
t1,t2)的的委托
T
i
T_i
Ti,然后通过检查
t
(
X
)
t(X)
t(X)在随机点
x
x
x上的值,使验证者相信它对
t
(
X
)
t(X)
t(X)的系数有承诺:

验证:
为了构造一个
a
R
∘
y
n
{\rm a}_R\circ{\rm y}^n
aR∘yn的承诺,验证者将承诺的生成元从
h
{\rm h}
h变为
h
′
=
h
(
y
−
n
)
{\rm h}'={\rm h}^{({\rm y}^{-n})}
h′=h(y−n)。这产生了了这样的效果:
A
A
A现在是
(
a
L
,
a
R
∘
y
n
)
({\rm a}_L,{\rm a}_R\circ{\rm y}^n)
(aL,aR∘yn)相对于新的生成元
(
g
,
h
′
,
h
)
({\rm g},{\rm h}',h)
(g,h′,h)的向量承诺;类似地,
S
S
S是
(
s
L
,
s
R
∘
y
n
)
({\rm s}_L,{\rm s}_R\circ{\rm y}^n)
(sL,sR∘yn)的向量承诺。
验证过程:

(上文提到,等式右边是多项式系数
t
0
,
t
1
,
t
2
t_0,t_1,t_2
t0,t1,t2的承诺,所以验证时还需要等式右边的承诺(line 67),即
l
(
x
)
,
r
(
x
)
l(x),r(x)
l(x),r(x),而
r
(
x
)
r(x)
r(x)有两个hadamard product的承诺需构造。
line 66:
A
⋅
S
x
A\cdot S^x
A⋅Sx构造
l
(
x
)
,
r
(
x
)
l(x),r(x)
l(x),r(x)中与
a
L
,
a
R
,
s
L
,
s
R
{\rm a}_L,{\rm a}_R,{\rm s}_L,{\rm s}_R
aL,aR,sL,sR有关的项(line 58-59绿色部分),其余的是其他项的承诺
)
对数范围证明
上面给出的范围证明的规模是
O
(
n
)
O(n)
O(n),可利用改进的内积证明将其降到
O
(
l
o
g
n
)
O({\rm log} n)
O(logn),即,证明中用内积证明代替传递
l
,
r
{\rm l,r}
l,r。
(67-68)等同于验证关系(2),Protocol 2的输入:
(
g
,
h
′
,
P
h
−
μ
,
t
^
)
({\rm g},{\rm h}',Ph^{-\mu},\hat{t})
(g,h′,Ph−μ,t^),内积证明仅传递
2
⋅
⌈
l
o
g
2
(
n
)
⌉
+
2
2\cdot \lceil {\rm log}_2(n) \rceil+2
2⋅⌈log2(n)⌉+2个元素(每轮一对
L
,
R
∈
G
L,R\in\mathbb{G}
L,R∈G,最后一轮传递
a
,
b
∈
Z
p
a,b\in\mathbb{Z}_p
a,b∈Zp),整个range proof共传递
2
⋅
⌈
l
o
g
2
(
n
)
⌉
+
4
2\cdot \lceil {\rm log}_2(n) \rceil+4
2⋅⌈log2(n)⌉+4个群元素(
T
1
,
T
2
,
A
,
S
∈
G
T_1,T_2,A,S\in\mathbb{G}
T1,T2,A,S∈G)和5个
Z
p
\mathbb{Z}_p
Zp元素(
τ
x
,
μ
,
t
^
\tau_x,\mu,\hat{t}
τx,μ,t^)。
聚合对数证明
即将多个range proof聚合为一个证明。关系:
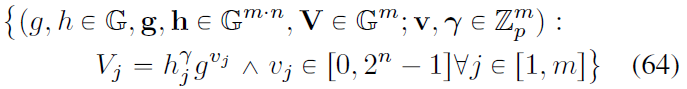
调整证明:
- (line 41): a L ∈ Z p n ⋅ m , ⟨ 2 n , a L [ ( j − 1 ) ⋅ n : j ⋅ n − 1 ] ⟩ = v j , j ∈ [ 1 , m ] {\rm a}_L\in\mathbb{Z}_p^{n\cdot m},\left\langle {\bm 2}^n, {\rm a}_{L[(j-1)\cdot n:j\cdot n-1]}\right\rangle=v_j,j\in[1,m] aL∈Zpn⋅m,⟨2n,aL[(j−1)⋅n:j⋅n−1]⟩=vj,j∈[1,m],故而 a L {\rm a}_L aL是每个 v j v_j vj的按位连接。
- 调整
l
(
X
)
,
r
(
X
)
l(X),r(X)
l(X),r(X):
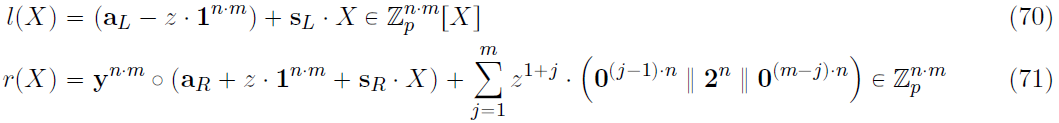
- 计算
τ
x
\tau_x
τx
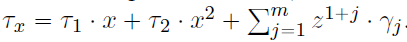
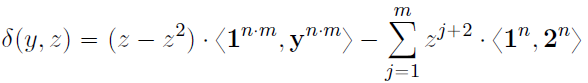
- (line 65):需包含所有的
V
j
V_j
Vj承诺:
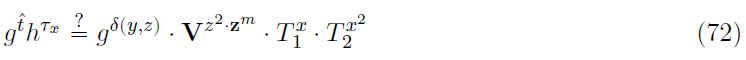
-
P
P
P的定义:
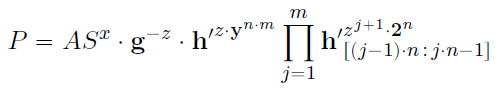
整个聚合的range proof共传递 2 ⋅ ⌈ l o g 2 ( n ⋅ m ) ⌉ + 4 2\cdot \lceil {\rm log}_2(n\cdot m) \rceil+4 2⋅⌈log2(n⋅m)⌉+4个群元素和5个 Z p \mathbb{Z}_p Zp元素。相比于m个独立的范围证明,聚合的范围证明仅增加一个 2 ⋅ l o g 2 ( m ) 2\cdot{\rm log}_2(m) 2⋅log2(m)大小的附加项:
- 2 ⋅ l o g 2 ( n ⋅ m ) + 4 = 2 ⋅ l o g 2 ( n ) + 4 + 2 ⋅ l o g 2 ( m ) 2\cdot {\rm log}_2(n\cdot m)+4=2\cdot {\rm log}_2(n)+4+2\cdot{\rm log}_2(m) 2⋅log2(n⋅m)+4=2⋅log2(n)+4+2⋅log2(m)
- [ 2 ⋅ l o g 2 ( n ) + 4 ] ⋅ m [2\cdot {\rm log}_2(n)+4]\cdot m [2⋅log2(n)+4]⋅m.
通过Fiat-Shamir转换成非交互证明
即所有挑战都被hash取代。例如,可以设 y = H ( s t , A , S ) , z = H ( A , S , y ) y={\rm H}({\rm st},A,S),z={\rm H}(A,S,y) y=H(st,A,S),z=H(A,S,y), s t {\rm st} st是statement,对于范围证明, s t {\rm st} st是 { V , n } \{V,n\} {V,n}. 必须将statement包含在hash的输入中,否则敌手可能会证明statement无效.
Frozen Heart
Trail of Bits公开披露了一些关键的漏洞(“Frozen Heart”),这些漏洞破坏了零知识证明系统的多个实现的可靠性(包括BulletProofs),是由不安全的Fiat-Shamir转换实现造成的,该转换允许恶意用户伪造随机statement的证明。
Fiat-Shamir转换应用于这样结构的证明系统:
- Prover: commitment
- Verifier: challenge
- Prover: response(proof)
对于这种结构的证明系统,一个非常重要的假设是,验证者产生的挑战值是被证明者完全无法预测和控制的。在高层次上,原因是证明者生成的零知识证明只有在满足非常具体的数学关系时才被认为是有效的,证明者通过以下两种之一的方式满足这个关系:
- 他实际上拥有满足关系所需的秘密数据,并以诚实的方式生成零知识证明。
- 他没有必要的秘密数据,但他猜测随机值,并且很幸运。
对于一个安全的证明系统,只要随机挑战是完全不可预测的,恶意证明者就不可能出现第二种情况;但如果恶意的证明者能以某种方式预测出这个值,只要找到符合数学关系的随机值,就很容易伪造证明。这就是Frozen Heart漏洞工作的原理。
防止Frozen Heart
严格遵守Fiat-Shamir转换的法则:hash计算必须包括来自零知识证明statement的所有公共值和证明中计算的所有公共值(即所有随机承诺值)。
这个漏洞直接威胁到几乎所有使用Fiat-Shamir变换的证明系统,着实非常严重。Jim Miller分析出现这个问题的原因:大多数学术论文只提供交互版本的协议,然后顺便提到,可以使用Fiat-Shamir转换使其非交互,但很少说明应该如何使用这种技术!(这部分很有意思,建议直接看原文)
BulletProofs中的Frozen Heart漏洞
BulletProofs给出了交互式证明,而Frozen Heart的影响它转换为非交互证明的Fiat-Shamir转换:在line(49-50)(55-56)中,生成三个不同的Fiat-Shamir challenges x , y , z x,y,z x,y,z,在BulletProofs的原始版本中, y = H ( A , S ) , z = H ( A , S , y ) , x = ( A , S , y , z , T 1 , T 2 ) y={\rm H}(A,S),z={\rm H}(A,S,y),x=(A,S,y,z,T_1,T_2) y=H(A,S),z=H(A,S,y),x=(A,S,y,z,T1,T2)(这个是根据算法推出的,包括了挑战 x x x之前所有公共传递的随机承诺,挑战值),在Jim Miller的提示下,Bulletproofs的作者已在最新的 full version中进行了改正。
漏洞:没有包含所有的公共值(尤其是随机承诺
V
V
V),故而它允许恶意证明者伪造实际位于预定义范围之外的值的证明。
恶意的证明者可以利用这个漏洞:
- 设 v v v等于范围内的任意值。假设 v = 3 v = 3 v=3。(假设预定义的范围为 v ∈ [ 0 , 2 32 ) v\in[0,2^{32}) v∈[0,232).)
- 选择一个随机的 γ \gamma γ值。
- 使用 v , γ v,\gamma v,γ按照预期(根据(41),(42),(44),(47))生成 a L , a R , A , S {\rm a}_L, {\rm a_R}, A,S aL,aR,A,S.
- 按照要求计算 t 1 , t 2 t_1,t_2 t1,t2,并通过随机采样取 t 1 ′ , t 2 ′ t_1',t_2' t1′,t2′,在计算 T 1 , T 2 T_1,T_2 T1,T2时,用 t 1 ′ , t 2 ′ t_1',t_2' t1′,t2′分别代替 t 1 , t 2 t_1,t_2 t1,t2,即 T i = ( g t i ′ ) ( h τ i ) T_i=(g^{t_i'})(h^{\tau_i}) Ti=(gti′)(hτi)。
- 根据协议计算剩余的值 ( l , r , t ^ , τ x , μ ) ({\rm l, r},\hat{t}, \tau_x, \mu) (l,r,t^,τx,μ)。
- 最后,计算一个新的 V V V,使用相同的 γ \gamma γ,但有一个新的 v ′ v' v′值: v ′ = 3 + ( t 1 − t 1 ′ ) ( x / z 2 ) + ( t 2 − t 2 ′ ) ( x 2 / z 2 ) v' = 3 + (t_1 - t_1')(x/z^2)+ (t_2 - t_2')(x^2/z^2) v′=3+(t1−t1′)(x/z2)+(t2−t2′)(x2/z2),其中 v = 3 v=3 v=3.
回顾这个计算过程:
- 计算出的与预期不同的值只有 T 1 , T 2 , v T_1,T_2,v T1,T2,v。由于我们按预期计算了其他值,所有检查都将自动通过,但检查(65)除外,它依赖于 T 1 , T 2 , v T_1,T_2,v T1,T2,v。
- 但是,由于
x
,
y
,
z
x,y,z
x,y,z的计算独立于
V
V
V,我们可以计算依赖于这些值的恶意
V
V
V值,并通过检查(65):
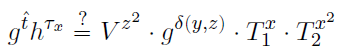
①等式左边: L H S = ( g t ^ ) ( h τ x ) = ( g [ t 0 + t 1 x + t 2 x 2 ] ) ( h [ τ 2 x 2 + τ 1 x + z 2 γ ] ) LHS = (g^{\hat{t}})(h^{\tau_x})= (g^{[t_0 + t_1 x + t_2 x^2]})(h^{[\tau_2 x^2 + \tau_1 x + z^2 \gamma]}) LHS=(gt^)(hτx)=(g[t0+t1x+t2x2])(h[τ2x2+τ1x+z2γ]).
②等式右边: R H S = ( V z 2 ) ( g δ ( y , z ) ) ( T 1 x ) ( T 2 x 2 ) = ( V z 2 ) ( g δ ( y , z ) ) [ ( g t 1 ′ ) ( h τ 1 ) ] x [ ( g t 2 ′ ) ( h τ 2 ) ] x 2 RHS = (V^{z^2})(g^{\delta(y,z)})(T_1^x)(T_2^{x^2}) = (V^{z^2})(g^{\delta(y,z)})[(g^{t_1'})(h^{\tau_1})]^x[(g^{t_2'})(h^{\tau_2})]^{x^2} RHS=(Vz2)(gδ(y,z))(T1x)(T2x2)=(Vz2)(gδ(y,z))[(gt1′)(hτ1)]x[(gt2′)(hτ2)]x2.
③现在,如果你看我们为 V V V取的 v ′ v ' v′值,你会发现 T 1 T_1 T1和 T 2 T_2 T2中 g g g的指数会消掉 V V V中 g g g的指数(消掉关于 t i ′ t_i' ti′的):
R H S = [ ( h γ g 3 + ( t 1 − t 1 ′ ) ( x / z 2 ) + ( t 2 − t 2 ′ ) ( x 2 / z 2 ) ) z 2 ] ( g δ ( y , z ) ) [ ( g t 1 ′ ) ( h τ 1 ) ] x [ ( g t 2 ′ ) ( h τ 2 ) ] x 2 RHS=[(h^\gamma g^{3 + (t_1 - t_1')(x/z^2)+ (t_2 - t_2')(x^2/z^2)})^{z^2}](g^{\delta(y,z)})[(g^{t_1'})(h^{\tau_1})]^x[(g^{t_2'})(h^{\tau_2})]^{x^2} RHS=[(hγg3+(t1−t1′)(x/z2)+(t2−t2′)(x2/z2))z2](gδ(y,z))[(gt1′)(hτ1)]x[(gt2′)(hτ2)]x2
= [ g [ 3 + ( t 1 − t 1 ′ ) ( x / z 2 ) + ( t 2 − t 2 ′ ) ( x 2 / z 2 ) ] ⋅ z 2 + t 1 ′ x + t 2 ′ x 2 ] [ h γ z 2 + τ 1 x + τ 2 x 2 ] =[g^{[3 + (t_1 - t_1')(x/z^2)+ (t_2 - t_2')(x^2/z^2)]\cdot z^2+t_1'x+t_2'x^2}][h^{\gamma z^2+\tau_1 x+\tau_2 x^2}] =[g[3+(t1−t1′)(x/z2)+(t2−t2′)(x2/z2)]⋅z2+t1′x+t2′x2][hγz2+τ1x+τ2x2]
= [ g [ 3 z 2 + t 1 x + t 2 x 2 + δ ( y , z ) ] ] [ h γ z 2 + τ 1 x + τ 2 x 2 ] =[g^{[3z^2 + t_1x+t_2x^2+\delta(y,z)]}][h^{\gamma z^2+\tau_1 x+\tau_2 x^2}] =[g[3z2+t1x+t2x2+δ(y,z)]][hγz2+τ1x+τ2x2].
④等式左边有 t 0 + t 1 x + t 2 x 2 t_0 + t_1 x + t_2 x^2 t0+t1x+t2x2,而等式右边有 3 z 2 + t 1 x + t 2 x 2 + δ ( y , z ) 3z^2 + t_1x+t_2x^2+\delta(y,z) 3z2+t1x+t2x2+δ(y,z)作为 g g g的指数。 t 0 t_0 t0在原文中的定义为:
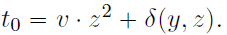
完全正确,也就是说成功伪造了证明。
注意,这是一个新提交的 V V V的证明,其中 v v v被设为 v ′ = 3 + ( t 1 − t 1 ′ ) ( x / z 2 ) + ( t 2 − t 2 ′ ) ( x 2 / z 2 ) v'= 3 + (t_1 - t_1')(x/z^2)+ (t_2 - t_2')(x^2/z^2) v′=3+(t1−t1′)(x/z2)+(t2−t2′)(x2/z2),因为 y , z y,z y,z是随机Fiat-Shamir挑战,所以 v ′ v' v′最终会在区间 [ 0 , g r o u p o r d e r ) [0,{\rm group order}) [0,grouporder)中,而group order通常会比要证明的区间大得多,所以 v ′ v' v′会以压倒性的优势处于要证明的区间之外而证明仍然通过。而如果 v ′ v' v′在这个区间内,则恶意证明者可以重新选择一些随机值再运行这个过程,直到获得他想要的 v ′ v' v′值。






















 2353
2353











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








