Bulletproofs: Short Proofs for Confidential Transactions and More学习笔记

1. 引言

Benedikt B¨unz、 Jonathan Bootle和 Dan Boneh等人2018年论文《Bulletproofs: Short Proofs for Confidential Transactions and More》中：

• 提出了Bulletproofs算法——基于discrete logarithm assumption，无需trusted setup，具有short proofs的NIZK算法。（采用Fiat-Shamir heuristic来实现non-interactive。）Bulletproofs尤其适合用于为committed values提供range proofs：
  – 证明a committed value is in a range，仅需要 $2{\log }_2(n)+9$ group 和 field elements，其中$n$为range的bit length。
  – Proof generation和verification time均为$O(n)$。

• 现有Bitcoin及其它加密货币隐私交易的range proof size为$O(n)$，Bulletproofs将其提高至 $2{\log }_2(n)+9$。

• Bulletproofs支持对多个range proofs的aggregation，
  – 为了证明来自同一party的$m$个commitments lie in a given range，可将其aggregate 为 a single proof，并仅需额外再增加$O(\log (m))$ 个group elements。
  – 为了aggregate proofs from multiple parties，we enable the parties to generate a single proof without revealing their inputs to each other via a simple multi-parity computation (MPC) protocol for constructing Bulletproofs。该多方安全计算协议可为：1）具有constant number of rounds and linear communication或者2）具有a logarithmic number of rounds and logarithmic communication。以CoinJoin混币方案（Maxwell 2013年《 CoinJoin: Bitcoin privacy for the real world》）为例，隐私交易的inputs来自多个parties，可借助MPC protocol，allow multiple parties with secret committed values to jointly generate a single range proof for all their values, without revealing their secret values to each other。

• 尽管Bulltproofs的verification time为$O(n)$，但实际是足够高效的。同时，支持对多个Bulletproofs仅需batch verify，从而进一步提升verify速度。
  verify an aggregation of 16 range proofs的时间与verify 16个ECDSA signatures的时间相当。

Bulletproofs构建在Bootle和Groth等人2016年论文《Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting》算法基础之上，做了如下改进：

• 将其中的inner product argument的communication complexity降低了3倍。
• 构建range proofs时，在最后一轮无需为Verifier提供commitment openings。

除了用于range proofs，Bulletproofs还可用于：

• 为arithmetic circuit提供基于discrete logarithm assumption 无需trusted setup的short 零知识证明算法。其proof size 为$O(\sqrt{N})$，其中$N$为multiplication gate的数量。
• verifiable shuffle。

本文对应的代码实现有：

• https://github.com/dalek-cryptography/bulletproofs
• https://github.com/adjoint-io/bulletproofs
• https://github.com/lovesh/bulletproofs-r1cs-gadgets
• https://github.com/KZen-networks/bulletproofs
• https://github.com/akosba/jsnark

https://github.com/akosba/jsnark 中提供了一个通用工具，用于构建Bulletproofs for any NP language，该工具可读取Pinocchio格式的arithmetic circuit，同时包含了将C语言编译为circuit fomat 的编译器。

1.1 背景

基于区块链构建的加密货币支持点对点的价值交互，通过维护全局同步的分布式账本——blockchain。
任何人均可验证区块链中当前状态以及账本中所有交易的有效性。为此，Bitcoin 要求交易中的所有信息均是public的：

• the sender 交易发起方；
• the receiver 交易接收方；
• the amount transferred 交易金额。

所谓隐私支付包含2个属性：

• 1）anonymity 匿名性，即交易中的发起方和接收方的身份信息均需隐藏；
• 2）confidentiality 机密性，即交易金额需隐藏。

由于Bitcoin addresses与现实真实身份之间存在unlinkability，Bitcoin提供了弱的anonymity，但是缺少confidentiality。这制约了Bitcoin的一些应用。如雇员并不喜欢被用bitcoin来支付薪水，因为那样他们的薪水金额将发布到public blockchain中。

为了对交易金额实现隐藏，Maxwell 在2016年《Confidential transactions》提出了confidential transactions (CT) 概念，通过对每笔交易金额进行commit实现隐藏。这种方式似乎会影响blockchain的public validation，an observer不再能够判断交易的输入之和是否大于交易的输出之和，以及验证所有的交易输入/输出金额是否为正数。通过为每笔交易提供一个证明隐私交易有效性的证明可以解决该问题。

Poelstra等人在2017年 《 Confidential assets 》中指出，现有的隐私交易零知识证明要么非常大，要么需要trusted setup。

• 需要trusted succinct 零知识证明方案有：如 Ben-Sasson等人2013年论文《SNARKs for C: verifying program executions succinctly and in Zero Knowledge》和 Gennaro等人2013年论文《Quadratic span programs and succinct NIZKs without PCPs》 。要求每个人都信任setup过程运行正确。
• 不需要trusted setup的零知识证明方案有： Ben-Sasson等人2018年论文《Scalable, transparent, and post-quantum secure computational integrity》。其所构建的range proof size 比当前的方案还要大。

构建同时具有short proof size和不需要trusted setup的零知识证明方案，在加密货币领域很有价值。对于任何分布式系统，若proofs需要通过网络传输或者需要长期存储时，更短的proof size将有助于节约cost。

1.2 相关研究

1）现有的range proofs方案有：

• Maxwell 2016年《Confidential transactions》中提出了confidential transactions (CT) 概念，通过对每笔交易金额进行commit实现隐藏。这种方式似乎会影响blockchain的public validation，an observer不再能够判断交易的输入之和是否大于交易的输出之和，以及验证所有的交易输入/输出金额是否为正数——即在区间$[0,2^n]$，其中$2^n$远远小于group size。通过为每笔交易提供一个证明隐私交易有效性的证明可以解决该问题。
• [Poe] Poelstra 2016年《Mimblewimble》
• Maxwell和Poelstra 2015年《Borromean ring signatures》。
• Poelstra等人2017年《 Confidential assets 》中通过side-chains来实现隐私交易。
• Noether等人2016年《Ring confidential transactions》中提出了关注隐私的加密货币Monero。
• Andreev 2017年《Hidden in Plain Sight: Transacting Privately on a Blockchain》私有链中实现的隐私交易。

以上方案除[Poe] 外都是基于committed values 构建的range proofs，其proof size为$O(n)$，这些proof是隐私交易中size的主要贡献者。
现有的Maxwell 2016年《Confidential transactions》实现，对于仅有2个output，32bit精度的隐私交易其大小为5.4KB，而其中5KB是由range proof贡献的。尽管近期有做优化，但range proof大小仍占据3.8KB。

在本文写作时，Bitcoin有来自2200万笔交易的约5000万个UTXOs。使用52-bit 来表示bitcoin从1 satoshi到2100万bitcoin的数值，若使用现有的range proofs方案，大约需要160GB的range proof data。而若采用aggregated Bulletproofs，则将仅需小于17GB的空间，节约了大概10倍的空间。

2）现有的加密货币隐私交易方案有：

• 以CoinJoin混币方案（Maxwell 2013年《 CoinJoin: Bitcoin privacy for the real world》）为例，隐私交易的inputs来自多个parties，可借助MPC protocol，allow multiple parties with secret committed values to jointly generate a single range proof for all their values, without revealing their secret values to each other。无法建立transaction inputs 和 transaction outputs之间的联系。
• CoinShuffle [RMSK14] （Ruffing等人2014年论文《CoinShuffle: Practical decentralized coin mixing for Bitcoin》）在CoinJoinh混币方案的基础上，去除了对可信第三方的依赖，实现了完全去中心化的Bitcoin mixing protocol。
• Monero [Mon] （《Monero - Private Digital Currency》）为采用了密码学技术实现了强隐私保护的加密货币。借助的密码学技术有：
  – stealth address;
  – ring-signatures [vS13];
  – ring confidential transactions [NM+16]（Noether等人2016年论文《Ring confidential transactions》）。
• ZeroCash [BSCG+14] （Ben-Sasson等人2014年论文《 Zerocash: Decentralized anonymous payments from Bitcoin》） 中也提供了隐私保护交易可选项，但是需要expensive transaction generation cost且需要trusted setup。

1.3 Mimblewimble

[Poe] Poelstra 2016年《Mimblewimble》和 Jedusor 2016年 《Mimblewimble》 提出的Mimblewimble协议，可进一步节约存储空间。

• Jedusor 2016年 《Mimblewimble》中指出：对0的Pedersen commitment可看成是一个ECDSA的公钥，而对于一个有效的隐私交易，其 (inputs-outputs-transaction fees) 必须为0。A prover constructing a confidential transaction can therefore sign the transaction with the difference of the outputs and inputs as the public key. This small change removes the need for a scriptSig which greatly simplifies the structure of confidential transactions。

• Poelstra 2016年《Mimblewimble》在Jedusor的基础上进一步改进了Mimblewimble协议，所有的spent transactions can be pruned and new nodes can efficiently validate the entire blockchain without downloading any old and spent transactions，从而大幅简化了区块链。进一步优化，可实现高度压缩的区块链，仅需要包含一小部分区块头和剩余的unspent transaction outputs 以及相应的range proofs和 an un-prunable 32 bytes per transaction。
  Mimblewimble协议支持对多个transaction先aggregate，然后再发送给blockchain。

Mimblewimble blockchain会随着UTXO set 的size而增长，而若使用Bulletproofs，其仅随那些具有unspent outputs的transaction数量而增长，unspent outputs的transaction数量远远小于UTXO set 的size。
总之Bulletproofs不仅适于替代现有隐私交易中的range proofs，同时也有助于帮助Mimblewimble成为实用的方案用于构建比现有Bitcoin blockchain更小的blockchain。

1.4 Provisions协议

Dagher等人在2015年论文《Privacy-preserving proofs of solvency for bitcoin exchanges (full version)》中提出了Provisions 协议，用于证明交易所可偿还能力。
该协议中依赖range proofs来防止插入负数金额的账户。当为a large exchange with 200万客户提供证明时需要约18GB的空间，而range proofs 将占据约13GB。
若用Bulletproofs协议替换Provisions协议中的NIZK proof时，the range proofs would take up less than 2KB, the proof for one commitment per customer 的size为62MB，从而将节约将近300倍的空间。

1.5 Verifiable shuffle

Verifiable shuffle是指：对于2组committed值$x_1,\cdots ,x_n$和$y_1,\cdots ,y_n$，证明第二组数据为第一组数据的permutation。

verifiable shuffle可用于voting，mixnets以及可偿还能力证明。

verifiable shuffle的衍化有：

• [Nef01] Nef 2001年论文《A verifiable secret shuffle and its application to e-voting》中给出了一个实用的verifiable shuflle实现；
• [Gro03,GI08a] Groth 2003年论文《A verifiable secret shuffle of homomorphic encryptions》和Groth等人2008年论文《Sub-linear zero-knowledge argument for correctness of a shuffle》对此进行了改进；（参见博客 A Verifiable Secret Shuffle of Homomorphic Encryptions学习笔记）
• [BG12] 2012年论文《Efficient Zero-Knowledge Argument for Correctness of a Shuffle》是当前效率最高的实现，具有的communication complexity为$O(\sqrt{n})$。（参见博客 Efficient Zero-Knowledge Argument for Correctness of a Shuffle学习笔记（1） ）

若使用Bulletproofs来实现verifiable shuffle，其size可降至$O(\log n)$——通过sorting circuit 对两组list进行排序，并验证排序后的两组数据相等。该sorting circuit使用$O(n\cdot \log (n))$个乘法门，具有的proof size仅为$O(\log (n))$。构建proof和验证的时间为$O(n)$。

1.6 智能合约的NIZK proofs

以太坊系统通过使用高度表达的智能合约来实现复杂交易。智能合约与其它区块链交易类似，都是public无法提供内在隐私保证。
为了使智能合约具有隐私保护功能，为其引入了NIZK proofs，使得用户输入信息不被泄露，相关的研究有：

• Kosba等人2016年论文《 Hawk: The blockchain model of cryptography and privacy-preserving smart contracts》
• McCorry 2017年论文《A smart contract for boardroom voting with maximum voter privacy》
• Campanelli 等人2017年论文《 Zero-knowledge contingent payments revisited: Attacks and payments for services》

以上这些研究中的NIZK proof本身并不适合通过智能合约来verify，因为区块链与智能合约之间的communication是expensive的，且智能合约本身的计算能力也非常有限。

• SNARKs具有succinct proofs和efficient verifiers，似乎是个不错的选择，但是当前实用的SNARKs（Ben-Sasson等人2013年论文《SNARKs for C: verifying program executions succinctly and in Zero Knowledge》）需要复杂的trusted setup过程，这导致common reference string (CRS)很长，且每个应用需有针对的CRS并具有trapdoors。
  比如在Kosba等人2016年论文《 Hawk: The blockchain model of cryptography and privacy-preserving smart contracts》中，需要为每个智能合约创建不同的CRS，需要借助可信第三方或者昂贵的安全多方计算来创建这些CRS。
• 对于像McCorry 2017年论文《A smart contract for boardroom voting with maximum voter privacy》这样的特定应用，可通过经典的sigma protocols来构建零知识证明，但是相应的proof-size和expensive verification cost将限制其用于更复杂的场景。
• Campanelli 等人2017年论文《 Zero-knowledge contingent payments revisited: Attacks and payments for services》中提出了对Bitcoin进行zero-knowledge contingent payments (ZKCPs)，同时解决了Max 2011年论文《Zero knowledge contingent payment》中存在的攻击问题。ZKCPs允许trustless,atomic和efficient exchange of a cryptocurrency vs. some digital good。ZKCPs仅适于a single designated verifier，不支持public verification。当智能合约有多于两个用户时，ZKCPs将不适合。

Bulletproofs不需要trusted setup，具有small proof，但是Bulletproofs的verify不便宜，可以通过以下方式来规避：

• 仅在有人challenge时，smart contract才验证该proof是否正确。激励措施可保证理智的参与方不伪造proof，也不challenge a correct proof。
  也可以借鉴 [BGB17,TR] 中引入交互 referee delagation机制 [CRR11] 来进一步优化。即Prover在提供proof的同时，也提供 a succinct commitment to the verifier’s execution trace。若a challenger不同意该proof，也需要提供a commitment of his computation trace。然后两方参与通过二进制交互搜索来找到这两组computation的第一个分歧点。该协议的一个有趣的地方在于：若a proof is challenged，smart contract仅需验证a single computation step，如 a single gate of the verification circuit。
  将其与Bulletproofs结合使用，可实现more complex but privacy preserving smart contracts。

与其它NIZK proofs可受益于MPC protocol类似，Bulletproofs也可以分布式生成。以拍卖smart contract为例，竞拍者在第一轮将其竞拍金额的commitment发送出去，然后在第二轮open 该commitment。可通过NIZK proof来证明竞拍金额在一定范围里，而不需要reveal。
采用Bulletproofs’ MPC方案，多个竞拍者可以将其Bulletproofs combine为a single proof，从而可以隐藏竞拍者与竞拍金额之间的关联。

1.7 为Arithmetic circuit构建NIZK proof without trusted setup

Common reference string (CRS) 应对Prover和Verifier均已知，在没有CRS的情况下，不可能为general statements构建non-interactive zero-knowledge protocols。

当前为arithmetic circuit satisfiability构建的NIZK proofs有：

• Silvio Mical 1994年论文《Cs proofs》
• Kilian等人1995年论文《An efficient non-interactive zero-knowledge proof system for NP with general assumptions》
• Groth等人2008年论文《 Efficient non-interactive proof systems for bilinear groups》
• Gennaro等人2013年论文《Quadratic span programs and succinct NIZKs without PCPs》
• Ben-Sasson等人2013年论文《SNARKs for C: verifying program executions succinctly and in Zero Knowledge》
• Ben-Sasson等人2018年论文《Scalable, transparent, and post-quantum secure computational integrity》

以上这些方案除了性能不同之外，其CRS的complexity也不同。Ben-Sasson等人2013年论文《SNARKs for C: verifying program executions succinctly and in Zero Knowledge》中的算法具有highly structured，and sometimes feature a trapdoor，while some are simply chosen uniformly at random。

Security proofs假设CRS为honestly generated，实际上，CRS可由可信第三方或者通过安全多方计算协议来生成。借助安全多方计算协议，可减轻对embedded trapdoors的关注，如Ben-Sasson等人2014年论文《 Zerocash: Decentralized anonymous payments from Bitcoin》中借助trusted setup ceremony来生成public parameters。

SNARKs有大量研究成果，如：

• Groth 2010年论文《Short pairing-based non-interactive zero-knowledge arguments》
• Bitansky等人2012年论文《From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again》
• Gennaro等人2013年论文《Quadratic span programs and succinct NIZKs without PCPs》
• Bitansky等人2013年论文《Recursive composition and bootstrapping for SNARKS and proof-carrying data》
• Parno等人2016年论文《 Pinocchio: nearly practical verifiable computation》
• Ben-Sasson等人2013年论文《SNARKs for C: verifying program executions succinctly and in Zero Knowledge》
• Groth 2016年论文《On the size of pairing-based non-interactive arguments》

以上这些SNARKs可生成constant-sized proofs for any statement，同时具有非常快的verification time。但是：

• 他们都需要复杂的CRS，需要lengthy and computationally intensive protocols to generate distributively。（如 Bowe等人2017年论文《A multi-party protocol for constructing the public parameters of the pinocchio zk-snark》）
• 他们都依赖于strong unfalsifiable assumptions，如knowledge-of-exponent assumption。

另外，若CRS为随机生成的，就如$\pi$的数字或者假设hash函数behave like a random oracle。现有的不需要trusted setup的NIZK proof有：

• Silvio Mical 1994年论文《Cs proofs》
• Bootle等人2016年论文《Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting》（可参见博客 Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting学习笔记）
• Bootle等人2017年论文《Linear-time zero-knowledge proofs for arithmetic circuit satisfiability》
• Ben-Sasson等人2017年论文《 Computational integrity with a public random string from quasi-linear pcps》
• Ben-Sasson等人2018年论文《Scalable, transparent, and post-quantum secure computational integrity》

对于无需trusted setup的NIZK proof，Ben-Sasson等人的研究路线是：

• 2017年论文 [BCG+17a] 《Interactive oracle proofs with constant rate and query complexity》中提出了一种叫做Scalable Computational Integrity (SCI) 的proof system，并在2017年论文 [BSBC+17] 《 Computational integrity with a public random string from quasi-linear pcps》中对其进行了实现。SCI具有简单的setup，仅需依赖collision-resistant hash函数，SCI proof system 不是zero-knowledge的，性能表现比 [BSCG+13, BCC+16]还差。对于中等规模的circuit，SCI proof size大约在42MB。
• Ben-Sasson等人2018年论文《Scalable, transparent, and post-quantum secure computational integrity》提出了STARKs方案。STARKs为zero-knowledge，运行效率优于SCI，但是对于$2^{17}$ size 60-bit security 的circuit，STARKs的proof size将超过200KB，且随着size logarithmically增长。

对于$2^{17}$ size 120-bit security 的circuit，Bulletproofs的proof size仅有约1KB。而构建STARKs需要大量的内存，因为STARKs为提供prove效率，引入了大量的FFT计算。

• [AHIV17] 2017年Ames等人论文《Ligero: Lightweight sublinear arguments without a trusted setup》中基于MPC提出了具有linear verification time和$O(\sqrt{n})$ proof size的proof system。
• [WTs+] Wahby等人2018年论文《Doubly-efficient zksnarks without trusted setup》基于proof for muggles （参见2008年论文[GKR08] 《Delegating computation: interactive proofs for muggles》）和sub-linear polynomial commitment scheme构建了具有$O(\sqrt{n})$ verifier complexity和$O(\sqrt{n})$ proof size的zero-knowledge proof system。（参见博客 Hyrax: Doubly-efficient zkSNARKs without trusted setup学习笔记）

2. 密码学假设及一些定义

2.1 基于的Discret Log Relation假设

Discret Log Relation假设与Discret log assumption等价。

2.2 一些定义

• Commitment定义：
  

• Commitment的加法同态属性：
  

• Commitment的hiding属性：
  

• Commitment的binding属性：
  

• Pedersen Commitment定义：
  

• Pedersen Vector Commitment定义：
  

• zero-knowledge arguments of knowledge相关定义：
  
  
  

• zero-knowledge range proof定义：
  

• 其它约定：
  
  

3. Inner product argument

参看博客 Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting学习笔记，本文对Bootle等人2016年论文《Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting》的inner product argument算法进行了改进：

• Communication complexity 由 $6{\log }_2(n)$降为了 $2{\log }_2(n)$，其中$n$为vector dimension。

Bootle 2016方案中的基本信息表达为：

• public info：$z\in {\mathbb{Z}}_p,A,B\in \mathbb{G},\vec{g},\vec{h}\in {\mathbb{G}}^n$
• private info：$\vec{a},\vec{b}$
• relation：$A={\vec{g}}^{\vec{a}}\wedge B={\vec{h}}^{\vec{b}}\wedge \vec{a}\cdot \vec{b}=z$

本文通过对待证明relation的修改，使得communication complexity 由 $6{\log }_2(n)$降为了 $2{\log }_2(n)$。（注意此处的inner product为sound的，但不是zero-knowledge的）
本文的基本信息表达为：

• public info：$c\in {\mathbb{Z}}_p,P\in \mathbb{G},\vec{g},\vec{h}\in {\mathbb{G}}^n$
• private info：$\vec{a},\vec{b}$
• relation：$P={\vec{g}}^{\vec{a}}{\vec{h}}^{\vec{b}}\wedge \vec{a}\cdot \vec{b}=c$

进一步等价表达为：

• public info：$u,P\in \mathbb{G},\vec{g},\vec{h}\in {\mathbb{G}}^n$
• private info：$\vec{a},\vec{b}$
• relation：$P={\vec{g}}^{\vec{a}}{\vec{h}}^{\vec{b}}\cdot u^{<\vec{a}\cdot \vec{b}>}$

相应的relation等价协议表示为：


定义一个hash函数：
$H:{\mathbb{Z}}_p^{2n+1}\to \mathbb{G}$
设置$n^{\prime }=n/2$，generators $\vec{g},\vec{h}\in {\mathbb{G}}^n,u\in \mathbb{G}$
假设该hash函数的输入为：${\vec{a}}_1,{\vec{a}}_2^{\prime },{\vec{b}}_1,{\vec{b}}_2^{\prime }\in {\mathbb{Z}}_p^{n^{\prime }},c\in {\mathbb{Z}}_p$，输出为：
$H({\vec{a}}_1,{\vec{a}}_2^{\prime },{\vec{b}}_1,{\vec{b}}_2^{\prime },c)={\vec{g}}_{[:n^{\prime }]}^{{\vec{a}}_1}\cdot {\vec{g}}_{[n^{\prime }:]}^{{\vec{a}}_2^{\prime }}\cdot {\vec{h}}_{[:n^{\prime }]}^{{\vec{b}}_1}\cdot {\vec{h}}_{[n^{\prime }:]}^{{\vec{b}}_2^{\prime }}\cdot u^c\in \mathbb{G}$

对于此时待证明的relation $P$，可将其表达为是hash 函数的输出：（其中$\vec{a}={\vec{a}}_{[:n^{\prime }]}||{\vec{a}}_{[n^{\prime }:]},\vec{b}={\vec{b}}_{[:n^{\prime }]}||{\vec{b}}_{[n^{\prime }:]}$）
$P=H({\vec{a}}_{[:n^{\prime }]},{\vec{a}}_{[n^{\prime }:]},{\vec{b}}_{[:n^{\prime }]},{\vec{b}}_{[n^{\prime }:]},<\vec{a},\vec{b}>)$
可看出，该hash函数具有加法同态属性：
$H({\vec{a}}_1,{\vec{a}}_1^{\prime },{\vec{b}}_1,{\vec{b}}_1^{\prime },c_1)\cdot H({\vec{a}}_2,{\vec{a}}_2^{\prime },{\vec{b}}_2,{\vec{b}}_2^{\prime },c_2)=H({\vec{a}}_1+{\vec{a}}_2,{\vec{a}}_1^{\prime }+{\vec{a}}_2^{\prime },{\vec{b}}_1+{\vec{b}}_2,{\vec{b}}_1^{\prime }+{\vec{b}}_2^{\prime },c_1+c_2)$
$H({\vec{a}}_1,{\vec{a}}_1^{\prime },{\vec{b}}_1,{\vec{b}}_1^{\prime },c_1{)}^{x_1}\cdot H({\vec{a}}_2,{\vec{a}}_2^{\prime },{\vec{b}}_2,{\vec{b}}_2^{\prime },c_2{)}^{x_2}=H(x_1{\vec{a}}_1+x_2{\vec{a}}_2,x_1{\vec{a}}_1^{\prime }+x_2{\vec{a}}_2^{\prime },x_1{\vec{b}}_1+x_2{\vec{b}}_2,x_1{\vec{b}}_1^{\prime }+x_2{\vec{b}}_2^{\prime },x_1{c}_1+x_2{c}_2)$

基本的证明思路为：（二分法）

• Prover：针对$P=H({\vec{a}}_{[:n^{\prime }]},{\vec{a}}_{[n^{\prime }:]},{\vec{b}}_{[:n^{\prime }]},{\vec{b}}_{[n^{\prime }:]},<\vec{a},\vec{b}>)$，二分法计算：
  $L=H({\vec{0}}^{n^{\prime }},{\vec{a}}_{[:n^{\prime }]},{\vec{b}}_{[n^{\prime }:]},{\vec{0}}^{n^{\prime }},<{\vec{a}}_{[:n^{\prime }]},{\vec{b}}_{[n^{\prime }:]}>)$
  $R=H({\vec{a}}_{[n^{\prime }:]},{\vec{0}}^{n^{\prime }},{\vec{0}}^{n^{\prime }},{\vec{b}}_{[:n^{\prime }]},<{\vec{a}}_{[n^{\prime }:]},{\vec{b}}_{[:n^{\prime }]}>)$
  将$L,R\in \mathbb{G}$发送给Verifier。
• Verifier：发送random challenge $x\leftarrow {\mathbb{Z}}_p$。
• Prover：计算${\vec{a}}^{\prime }=x{\vec{a}}_{[:n^{\prime }]}+x^{-1}{\vec{a}}_{[n^{\prime }:]},{\vec{b}}^{\prime }=x^{-1}{\vec{b}}_{[:n^{\prime }]}+x{\vec{b}}_{[n^{\prime }:]}\in {\mathbb{Z}}_p^{n^{\prime }}$
  将${\vec{a}}^{\prime },{\vec{b}}^{\prime }\in {\mathbb{Z}}_p^{n^{\prime }}$发送给Verifier。
• Verifier：输入有$(L,R,{\vec{a}}^{\prime },{\vec{b}}^{\prime })$，计算$P^{\prime }=L^{(x^2)}\cdot P\cdot R^{x^{-2}}$，然后验证$P^{\prime }=H(x^{-1}{\vec{a}}^{\prime },x{\vec{a}}^{\prime },x{\vec{b}}^{\prime },x^{-1}{\vec{b}}^{\prime },<{\vec{a}}^{\prime },{\vec{b}}^{\prime }>)$是否成立。

利用加法同态性有：
$L^{(x^2)}\cdot P\cdot R^{x^{-2}}=H({\vec{a}}_{[:n^{\prime }]}+x^{-2}{\vec{a}}_{[n^{\prime }:]},x^2{\vec{a}}_{[:n^{\prime }]}+{\vec{a}}_{[n^{\prime }:]},{\vec{b}}_{[:n^{\prime }]}+x^2{\vec{b}}_{[n^{\prime }:]},x^{-2}{\vec{b}}_{[:n^{\prime }]}+{\vec{b}}_{[n^{\prime }:]},x^2<{\vec{a}}_{[:n^{\prime }]},{\vec{b}}_{[n^{\prime }:]}>+<\vec{a},\vec{b}>+x^{-2}<{\vec{a}}_{[n^{\prime }:]},{\vec{b}}_{[:n^{\prime }]}>)=H(x^{-1}{\vec{a}}^{\prime },x{\vec{a}}^{\prime },x{\vec{b}}^{\prime },x^{-1}{\vec{b}}^{\prime },<{\vec{a}}^{\prime },{\vec{b}}^{\prime }>)$

以上证明思路，proof为$(L,R,{\vec{a}}^{\prime },{\vec{b}}^{\prime })$，proof size为$n+2$个elements，相比于直接发送$\vec{a},\vec{b}$ 时的$2n$个elements，大约节约了一半的communication cost。

利用递归，可进一步降低communication cost：
根据$P^{\prime }=H(x^{-1}{\vec{a}}^{\prime },x{\vec{a}}^{\prime },x{\vec{b}}^{\prime },x^{-1}{\vec{b}}^{\prime },<{\vec{a}}^{\prime },{\vec{b}}^{\prime }>)=({\vec{g}}_{[:n^{\prime }]}^{x^{-1}}\circ {\vec{g}}_{[n^{\prime }:]}^x{)}^{{\vec{a}}^{\prime }}\cdot ({\vec{h}}_{[:n^{\prime }]}^x\circ {\vec{h}}_{[n^{\prime }:]}^{x^{-1}}{)}^{{\vec{b}}^{\prime }}\cdot u^{<{\vec{a}}^{\prime },{\vec{b}}^{\prime }>}$
相当于generators由$(\vec{g},\vec{h},u)$变为了$({\vec{g}}_{[:n^{\prime }]}^{x^{-1}}\circ {\vec{g}}_{[n^{\prime }:]}^x,{\vec{h}}_{[:n^{\prime }]}^x\circ {\vec{h}}_{[n^{\prime }:]}^{x^{-1}},u)$，对此可进行递归调用，进一步压缩proof size。
通过${\log }_{2}n$ round 调用，最终的communication cost为$2\lceil {\log }_2(n)\rceil$个group elements $\in \mathbb{G}$ 和2个Field elements $\in {\mathbb{Z}}_p$，Prover发送给Verifier的内容依次为：
$(L_1,R_1),\cdots ,(L_{{\log }_{2}n},R_{{\log }_{2}n}),a,b$
其中$a,b\in {\mathbb{Z}}_p$，会在最后一轮发送。

可借助Fiat-Shamir heuristic将以上证明过程转换为non-interactive，此时，Prover的主要计算压力在于 $8n$ 个group exponentiations，Verifier的主要为 $4n$个exponentiations。后续可进一步优化，使得Verifier仅需一个 size为 $2n+2\log (n)$的multi-exponentiation计算。

3.1 使用Multi-exponentiation对inner-product verification进行优化

在Protocol 2中，具有${\log }_2(n)$ round，在每个round，Prover和Verifier均需要计算一组新的generators ${\vec{g}}^{\prime },{\vec{h}}^{\prime }$。整个证明过程中这些新generators计算需要$4n$个exponentiations：在第一轮$2n$个，第二轮$\frac{2n}{2}$，在第$j$轮$\frac{n}{2^{j-1}}$个。
这就意味着，Verifier需要有$4n$个exponentiations计算，通过delay all the exponentiations到最后一轮，可进一步优化为使Verifier仅需一个 size为 $2n+2\log (n)$的multi-exponentiation计算。

假设$g,h$为最后一轮的generators，$x_j$为第$j$轮的challenge。
在最后一轮，Verifier会验证$g^a{h}^b{u}^{a\cdot b}=P$是否成立，其中$a,b\in {\mathbb{Z}}_p$是由Prover发送来的。
通过对整个递归过程进行展开，最终$g,h\in \mathbb{G}$可由原始的generators $\vec{g},\vec{h}\in {\mathbb{G}}^n$和challenges $(x_1,\cdots ,x_{{\log }_2(n)})$计算而来：
$g={\prod }_{i=1}^n{g}_i^{s_i}\in \mathbb{G},h={\prod }_{i=1}^n{h}_i^{1/s_i}\in \mathbb{G}$
其中$\vec{s}=(s_1,\cdots ,s_n)\in {\mathbb{Z}}_p^n$仅依赖于challenges $(x_1,\cdots ,x_{{\log }_2(n)})$。
scalars $s_1,\cdots ,s_n\in {\mathbb{Z}}_p$ 的计算公式为：
for $i=1,\cdots ,n:s_i={\prod }_{j=1}^{{\log }_2(n)}{x}_j^{b(i,j)}$
其中：
$b(i,j)=\{\begin{array}{c}1\text{ the }j\text{th bit of }i-1\text{ is }1\\ -1\text{ otherwise}\end{array}$

通过delay操作，最后一轮Verifier验证的公式变为：
${\vec{g}}^{a\cdot \vec{s}}\cdot {\vec{h}}^{b\cdot {\vec{s}}^{-1}}\cdot u^{a\cdot b}=P\cdot {\prod }_{j=1}^{{\log }_2(n)}{L}_j^{(x_j^2)}\cdot R_j^{(x_j^{-2})}$
以上公式中具有一个size为$2n+2{\log }_2(n)+1$的multi-exponentiation计算。而multi-exponentiation计算相比于分别计算$n$个独立的exponentiation要快得多。
【可参看博客 Updateable Inner Product Argument with Logarithmic Verifier and Applications 学习笔记 中采用结构化的generators来优化Verifier的工作量。】

4. 基于Bulletproofs构建具有logarithmic size的range proof

4.1 将range proof转换为inner product between two vectors

Bootle和Groth等人2016年论文《Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting》中提出了任意arithmetic circuit的proof system思路。（参见博客 Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting学习笔记）

range proof的基本信息表示为：

• public info：$g,h\in \mathbb{G},V\in \mathbb{G},n$
• private info：$v,\gamma \in {\mathbb{Z}}_p$
• relation：$V=h^{\gamma }{g}^v\wedge v\in [0,2^n-1]$

将数值$v$以$n$二进制位表示为 a ⃗ L = ( a 1 , ⋯   , a n ) ∈ { 0 , 1 } n \vec{a}_L=(a_1,\cdots,a_n)\in\{0,1\}^n a L​=(a1​,⋯,an​)∈{0,1}n，则有$<{\vec{a}}_L,{\vec{2}}^n>=v$，其中${\vec{2}}^n=(1,2,4,\cdots ,2^{n-1})$。同时也得保证${\vec{a}}_L$中的每个元素值均只能为0或者1，可表示为：
$<{\vec{a}}_L,{\vec{2}}^n>=v\wedge {\vec{a}}_R={\vec{a}}_L-{\vec{1}}^n\wedge {\vec{a}}_L\circ {\vec{a}}_R={\vec{0}}^n$

range proof的基本信息可进一步表示为：

• public info：$g,h\in \mathbb{G},\vec{g},\vec{h}\in {\mathbb{G}}^n,A,V\in \mathbb{G},n$
• private info：$v,\gamma ,\alpha \in {\mathbb{Z}}_p,{\vec{a}}_L,{\vec{a}}_R$
• relation：$V=h^{\gamma }{g}^v\wedge A=h^{\alpha }{\vec{g}}^{{\vec{a}}_L}{\vec{h}}^{{\vec{a}}_R}$ and $<{\vec{a}}_L,{\vec{2}}^n>=v\wedge {\vec{a}}_R={\vec{a}}_L-{\vec{1}}^n\wedge {\vec{a}}_L\circ {\vec{a}}_R={\vec{0}}^n$

接下来，需要将$<{\vec{a}}_L,{\vec{2}}^n>=v\wedge {\vec{a}}_R={\vec{a}}_L-{\vec{1}}^n\wedge {\vec{a}}_L\circ {\vec{a}}_R={\vec{0}}^n$中的$2n+1$个constraints以 random linear combination (chosen by the verifier) 的方式压缩为a single inner product constraint，然后使用Protocol 1来证明the inner product relation。

为了证明a committed vector $\vec{b}\in {\mathbb{Z}}_p^n$ 满足 $\vec{b}={\vec{0}}^n$，只需要Verifier发送random challenge $y\in {\mathbb{Z}}_p$，Prover证明$<\vec{b},{\vec{y}}^n>=0$。若$\vec{b}\ne {\vec{0}}^n$，则根据Schwartz-Zippel Lemma，$<\vec{b},{\vec{y}}^n>=0$等式成立的概率不高于$n/p$。所以若$<\vec{b},{\vec{y}}^n>=0$，则可让Verifier信服$\vec{b}={\vec{0}}^n$。
因此，Verifier发送random challenge $y\in {\mathbb{Z}}_p$，Prover需证明的relation可做如下转变：
${\vec{a}}_L\circ {\vec{a}}_R={\vec{0}}^n\Rightarrow <{\vec{a}}_L,{\vec{a}}_R\circ {\vec{y}}^n>=0$
${\vec{a}}_R={\vec{a}}_L-{\vec{1}}^n\Rightarrow {\vec{a}}_L-{\vec{a}}_R-{\vec{1}}^n={\vec{0}}^n\Rightarrow <{\vec{a}}_L-{\vec{a}}_R-{\vec{1}}^n,{\vec{y}}^n>=0$

Verifier在发送random challenge $z\in {\mathbb{Z}}_p$，将以上三个relation组合在一起，合并为一个待证明relation：
$z^2\cdot <{\vec{a}}_L,{\vec{2}}^n>+z\cdot <{\vec{a}}_L-{\vec{a}}_R-{\vec{1}}^n,{\vec{y}}^n>+<{\vec{a}}_L,{\vec{a}}_R\circ {\vec{y}}^n>=z^2\cdot v$ 【？？？是否可转为用polynomial commitment来证明？？？】

将上述等式转换为一个inner product来表示，同时保证inner product结果值为public info（$v$除外）：【基本思路为将public info表达式挪到一侧（$v$除外），同时有 ${\vec{y}}^n={\vec{y}}^n\circ {\vec{1}}^n,<{\vec{a}}_R,{\vec{y}}^n>=<{\vec{1}}^n,{\vec{a}}_R\circ {\vec{y}}^n>$。】
$<{\vec{a}}_L-z\cdot {\vec{1}}^n,{\vec{y}}^n\circ ({\vec{a}}_R+z\cdot {\vec{1}}^n)+z^2\cdot {\vec{2}}^n>=z^2\cdot v+\delta (y,z)$
其中$\delta (y,z)=(z-z^2)<{\vec{1}}^n,{\vec{y}}^n>-z^3<{\vec{1}}^n,{\vec{2}}^n>\in {\mathbb{Z}}_p$，Verifier可很容易计算出该值。

此时，Range proof基本信息为：

• public info：$g,h\in \mathbb{G},\vec{g},\vec{h}\in {\mathbb{G}}^n,A,V\in \mathbb{G},n,$
• Verifier challenges：$y,z\in {\mathbb{Z}}_p^{\ast }$
• private info：$v,\gamma ,\alpha \in {\mathbb{Z}}_p,{\vec{a}}_L,{\vec{a}}_R\in {\mathbb{Z}}_p^n$
• relation：$V=h^{\gamma }{g}^v\wedge A=h^{\alpha }{\vec{g}}^{{\vec{a}}_L}{\vec{h}}^{{\vec{a}}_R}$ and $<{\vec{a}}_L-z\cdot {\vec{1}}^n,{\vec{y}}^n\circ ({\vec{a}}_R+z\cdot {\vec{1}}^n)+z^2\cdot {\vec{2}}^n>=z^2\cdot v+\delta (y,z)$
  其中$\delta (y,z)=(z-z^2)<{\vec{1}}^n,{\vec{y}}^n>-z^3<{\vec{1}}^n,{\vec{2}}^n>\in {\mathbb{Z}}_p$

若Prover直接将以上inner product中的两个vectors $\vec{c}={\vec{a}}_L-z\cdot {\vec{1}}^n$和$\vec{d}={\vec{y}}^n\circ ({\vec{a}}_R+z\cdot {\vec{1}}^n)+z^2\cdot {\vec{2}}^n$ 直接发送给Verifier，Verifier可直接验证$Com(<\vec{c},\vec{d}>-\delta (y,z))=Com(v{)}^{z^2}$是否成立即可。
但是，直接发送vectors会泄露${\vec{a}}_L$信息，从而进一步泄露$v$值，为了解决该问题，需引入${\vec{s}}_L,{\vec{s}}_R\in {\mathbb{Z}}_p^n$来blind要发送的vectors。

借助Vector polynomials inner product来构建$\overrightarrow{l(X)},\overrightarrow{r(X)}\in {\mathbb{Z}}_p^n[X]$：
$\overrightarrow{l(X)}=({\vec{a}}_L-z\cdot {\vec{1}}^n)+{\vec{s}}_L\cdot X\in {\mathbb{Z}}_p^n[X]$
$\overrightarrow{r(X)}={\vec{y}}^n\circ ({\vec{a}}_R+z\cdot {\vec{1}}^n+{\vec{s}}_R\cdot X)+z^2\cdot {\vec{2}}^n\in {\mathbb{Z}}_p^n[X]$
$t(X)=<\overrightarrow{l(X)},\overrightarrow{r(X)}>=t_0+t_1\cdot X+t_2\cdot X^2\in {\mathbb{Z}}_p[X]$

可发现$t(X)$中的常量部分代表的即为待证明内容：
$<{\vec{a}}_L-z\cdot {\vec{1}}^n,{\vec{y}}^n\circ ({\vec{a}}_R+z\cdot {\vec{1}}^n)+z^2\cdot {\vec{2}}^n>=z^2\cdot v+\delta (y,z)$
其中$\delta (y,z)=(z-z^2)<{\vec{1}}^n,{\vec{y}}^n>-z^3<{\vec{1}}^n,{\vec{2}}^n>\in {\mathbb{Z}}_p$
而blinding vectors ${\vec{s}}_L$和${\vec{s}}_R$可保证Prover在发送$\overrightarrow{l(x)},\overrightarrow{r(x)},x\in {\mathbb{Z}}_p^{\ast }$时不会泄露任何的${\vec{a}}_L$和${\vec{a}}_R$信息。

$t(x)$的常量部分表示为$t_0$，接下来即需要Prover证明：
$t_0=z^2\cdot v+\delta (y,z)$
对系数$t_1,t_2$进行commitment，同时对任意的点$x\in {\mathbb{Z}}_p^{\ast }$，转为证明对多项式$t(X)$多项式的evaluation值确实为$t(x)$。
为此基本信息为：

• public info：$g,h\in \mathbb{G},\vec{g},\vec{h}\in {\mathbb{G}}^n,A,V,S\in \mathbb{G},n$ and $\vec{l},\vec{r}\in {\mathbb{Z}}_p^n,\hat{t}\in {\mathbb{Z}}_p$ and $T_1,T_2\in \mathbb{G}$
• Verifier challenges：$y,z,x\in {\mathbb{Z}}_p^{\ast }$
• private info：$v,\gamma ,\alpha \in {\mathbb{Z}}_p,{\vec{a}}_L,{\vec{a}}_R\in {\mathbb{Z}}_p^n,\rho \in {\mathbb{Z}}_p,{\vec{s}}_L,{\vec{s}}_R\in {\mathbb{Z}}_p^n$ and $t_1,t_2\in {\mathbb{Z}}_p,{\tau }_1,{\tau }_2\in {\mathbb{Z}}_p$
• relation：$V=h^{\gamma }{g}^v\wedge A=h^{\alpha }{\vec{g}}^{{\vec{a}}_L}{\vec{h}}^{{\vec{a}}_R}\wedge S=h^{\rho }{\vec{g}}^{{\vec{s}}_L}{\vec{h}}^{{\vec{s}}_R}\wedge T_1=h^{{\tau }_1}{g}^{t_1}\wedge T_2=h^{{\tau }_2}{g}^{t_2}\wedge \hat{t}=<\vec{l},\vec{r}>$ and $\vec{l}=\overrightarrow{l(x)}=({\vec{a}}_L-z\cdot {\vec{1}}^n)+{\vec{s}}_L\cdot x\in {\mathbb{Z}}_p^n$
  $\vec{r}=\overrightarrow{r(x)}={\vec{y}}^n\circ ({\vec{a}}_R+z\cdot {\vec{1}}^n+{\vec{s}}_R\cdot x)+z^2\cdot {\vec{2}}^n\in {\mathbb{Z}}_p^n$

注意：
有$A=Co{m}_{ck}({\vec{a}}_L,{\vec{a}}_R;\alpha )=h^{\alpha }{\vec{g}}^{{\vec{a}}_L}{\vec{h}}^{{\vec{a}}_R}=Co{m}_{c{k}^{\prime }}({\vec{a}}_L,{\vec{y}}^n\circ {\vec{a}}_R;\alpha )=h^{\alpha }{\vec{g}}^{{\vec{a}}_L}{\vec{h}}^{\prime ({\vec{y}}^n\circ {\vec{a}}_R)}$，其中${\vec{h}}^{\prime }={\vec{h}}^{{\vec{y}}^{-n}}=(h_1,h_2^{(y^{-1})},h_3^{(y^{-2})},\cdots ,h_n^{(y^{-n+1})})$
同理对$Co{m}_{c{k}^{\prime }}({\vec{s}}_L,{\vec{s}}_R\circ {\vec{y}}^n)$。
从而Verifier可利用commitment同态属性来进行验证：

4.2 实现range proof的inner product argument

相比于4.1节的直接发送整个$\vec{l},\vec{r}$ 长度为 $2\cdot n$个elements，可利用
第三节的Inner product argument实现logarithmic size $2\cdot \lceil {\log }_2(n)\rceil +2$个elements，最终整个range proof size为$2\cdot \lceil {\log }_2(n)\rceil +4$个elements in $\mathbb{G}$ 和 5个group elements in ${\mathbb{Z}}_p$。

注意此时的基本信息为：

• Public info：$(\vec{g},{\vec{h}}^{\prime },P{h}^{-\mu },\hat{t})$
• Private info：$\vec{l},\vec{r}$
• Relation：$\hat{t}=<\vec{l},\vec{r}>\wedge P{h}^{-\mu }={\vec{g}}^{\vec{l}}\cdot {\vec{h}}^{\prime \vec{r}}$

4.3 aggregate $m$个range proofs into one short proof

Dagher等人在2015年论文《Privacy-preserving proofs of solvency for bitcoin exchanges (full version)》中提出了Provisions 协议，用于证明交易所可偿还能力。Provision 协议中要求为每个账号金额均提供range proof。
所以，希望perform a proof for $m$ values which is more efficient than conducting $m$ individual range proofs。
relation表示为：

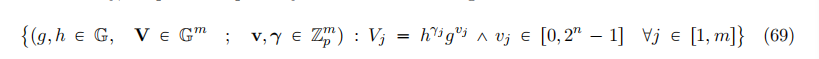
将$m$个values，每个value具有$n$ bits直接拼接在一起，然后为这$n\cdot m$ bits提供range proof，具体思路为：

相比于直接发送$n\cdot m$bits信息，利用Bulletproofs的inner product argument算法，对$m$个值的range proof size 可压缩为$2\cdot \lceil {\log }_2(n\cdot m)\rceil +4$个elements in $\mathbb{G}$ 和 5个group elements in ${\mathbb{Z}}_p$。这仅比单个value的range proof size 增加 $2\cdot {\log }_2(m)$ 个elements。

4.4 实现非交互式range proof

借助Fiat-Shamir heuristic，可将以上interactive protocol转换为non-interactive protocol，如$y=H(A,S),z=H(A,S,y)$。

同时，为了避免trusted setup，也可以用hash函数来生成public parameters $(\vec{g},\vec{h},g,h)$ from a small seed。该hash函数需要能map from { 0 , 1 } ∗ \{0,1\}^* {0,1}∗ to G ∖ { 1 } \mathbb{G}\setminus \{1\} G∖{1}，可基于2001年Boneh等人论文《 Short signatures from the weil pairing》中算法进行实现。或者也可以通过provide random access into the public parameters来实现，如使用a common random string。

4.5 MPC protocol for Bulletproofs

multiple parties may want to create a single joined confidential transaction, where each party knows some of the inputs and outputs and needs to create range proofs for their known outputs，满足 the joint transaction would not only be smaller than the sum of multiple transactions，同时可隐藏inputs与outputs的对应关系：
一种可实现方式是CoinJoin混币方案（Maxwell 2013年《 CoinJoin: Bitcoin privacy for the real world》）。

Dagher等人在2015年论文《Privacy-preserving proofs of solvency for bitcoin exchanges (full version)》中提出的Provisions 协议中，交易所需要将私钥分发给多台服务器，同时需要将用户数据库拆分为不同的chunks，但是仍能提供 a single short proof of solvency。

为了将来自于多方的range proofs aggregate 为 a single range proof，是否允许各方在补共享所有witness的情况下，生成一个Bulletproof？
解决方案之一是：采用安全多方计算技术来生成a single proof，但是可能会too expensive and incur significant communication costs。
因此，需要针对Bulletproofs专门设计一个简单的MPC协议。

注意4.3节的aggregate range proofs中，the inputs of one range proof do not affect the output of another range proof。
根据Bulletproofs的结构化特点，可理解为$m$ 方每方都有一个Pedersen commitment $(V_k{)}_{k=1}^m$，同时每方都可生成a single Bulletproof that each $V_k$ commits to a number in some fixed range。
存在两种实现方式：

• constant rounds，但communication cost与$m$和the binary encoding of the range均呈线性关系；
• logarithmic rounds，同时communication cost仅与$m$呈线性关系。

假设$m$为2的幂值，采用类似4.3节中的aggregate range proof表示，但是使用$k$来表示an index to denote the $k$th party’s message。$A^{(k)}$的生成方式与$A$类似，但是仅需要使用第$k$方的inputs。

整个为Bulletproofs设计的MPC protocol流程如下：

4.6 如何构建量子安全的range proof

Bulletproofs在discrete logarithm assumption下具有binding属性。对于加密货币来说，binding属性的破坏远比hiding属性影响更大，binding属性的破坏将导致空气币的产生。

需要注意：
discrete logarithm assumption仅对classical computers成立，对于量子计算机并不成立。

5. Arithmetic Circuits的zero-knowledge proof

Bootle和Groth等人2016年论文《Efficient Zero-Knowledge Arguments for Arithmetic Circuits in the Discrete Log Setting》中构建的arithmetic circuit proof size为 $6{\log }_2(n)+13$个elements（其中group elements $4{\log }_2(n)+7$个，field elements $2{\log }_2(n)+6$个，$n$为circuit中乘法门个数。）。
而本文通过对inner product argument的改进，可将arithmetic circuit proof size降为 $2{\log }_2(n)+13$个，同时为circuit增加了committed input wires 支持。

6. 对range proof的性能优化

• 采用3.1节类似的方式，将通过delay all the exponentiations到最后一轮，可进一步优化为使Verifier仅需一个 size为 $2n+2\log (n)+7$的multi-exponentiation计算。
  
• 计算scalars，针对上图（105）公式计算，计算challenge product方式改为：using only one multiplication in ${\mathbb{Z}}_p$ by applying batch inversion。
  
• 实现batch verification，基本思路为：
  为证明$g^x=1\wedge g^y=1$，则对任意的challenge $\alpha$，若$g^{\alpha \cdot x+y}=1$，则大概率$g^x=1\wedge g^y=1$成立。