学习笔记：One-Out-of-Many Proofs: Or How to Leak a Secret and Spend a Coin

Jens Groth and Markulf Kohlweiss《One-Out-of-Many Proofs: Or How to Leak a Secret and Spend a Coin》In: EUROCRYPT 2015
https://link.springer.com/content/pdf/10.1007%2F978-3-662-46803-6_9.pdf

$\Sigma$-Protocol for Commitment to 0 or 1

用$\Sigma$协议证明以下关系：

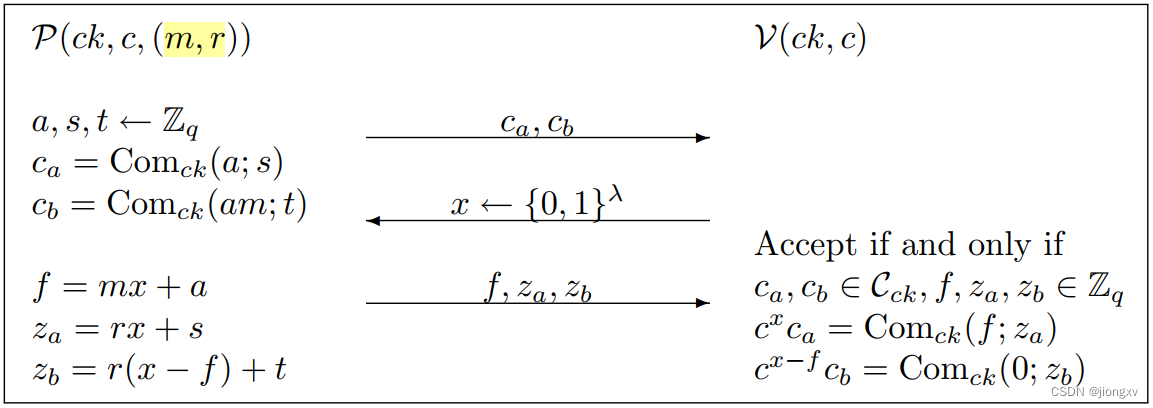
完整协议：

分析：

1. 验证公式1
   $$\begin{array}{rl}RHS& =Co{m}_{ck}(f;z_a)\\ & =Co{m}_{ck}(mx+a;rx+s)\\ & =Co{m}_{ck}(mx;rx)\cdot Co{m}_{ck}(a;s)\\ & =Co{m}_{ck}(m;r{)}^x\cdot c_a\end{array}$$
   当且仅当$c=Co{m}_{ck}(m;r)$时，等式成立。
2. 验证公式2
   $$\begin{array}{rl}RHS& =Co{m}_{ck}(0;z_b)\\ & =Co{m}_{ck}(0;r(x-f)+t)\\ & =Co{m}_{ck}(-am;r(x-f))\cdot Co{m}_{ck}(am;t)\\ & =Co{m}_{ck}(-am;r(x-f))\cdot c_b\end{array}$$
   要构造等式左边的形式，需要满足两个条件：
   ①$c=Co{m}_{ck}(m;r)$；
   ②$-am=m(x-f)$，当$m=0$时显然成立；若$m\ne 0$，则有$-a=x-f$，展开：
   $$\begin{array}{rl}-a& =x-mx-a\\ 0& =x-mx\\ & =x(1-m)\end{array}$$
   所以当$m=0,1$时，等式成立。

$\Sigma$-Protocol for One-out-of-N Commitment Containing 0

用 $\Sigma$-协议证明n个承诺中有一个对0的承诺，即证明关系：
R = { ( c k , ( c 0 , … , c N − 1 ) , ( ℓ , r ) ) c 0 , … , c N − 1 ∈ C c k  and  ℓ ∈ { 0 , … , N − 1 }  and  r ∈ Z q  and  c ℓ = Com ⁡ c k ( 0 ; r ) } R=\left\{\begin{array}{l|l}\left(c k,\left(c_{0}, \ldots, c_{N-1}\right),(\ell, r)\right) & \begin{array}{l}c_{0}, \ldots, c_{N-1} \in \mathcal{C}_{c k} \text { and } \ell \in\{0, \ldots, N-1\} \\ \text { and } r \in \mathbb{Z}_{q} \text { and } c_{\ell}=\operatorname{Com}_{c k}(0 ; r)\end{array}\end{array}\right\} R={(ck,(c0​,…,cN−1​),(ℓ,r))​c0​,…,cN−1​∈Cck​ and ℓ∈{0,…,N−1} and r∈Zq​ and cℓ​=Comck​(0;r)​​}

思路：
将要证明的命题等价转换：

• 存在一个index $l$，有：${\prod }_{i=0}^{N-1}{c}_i^{{\delta }_{i\ell }}$是一个0的承诺。其中${\delta }_{i\ell }$是Kronecker’s delta，即，${\delta }_{\ell \ell }=1$ and ${\delta }_{i\ell }=0$ for $i\ne \ell$
• 不失一般性，假设$N=2^n$，将$i,l$写成二进制： i = i 1 … i n ∈ { 0 , 1 } n i=i_{1} \ldots i_{n}\in\{0,1\}^n i=i1​…in​∈{0,1}n， ℓ = ℓ 1 … ℓ n ∈ { 0 , 1 } n \ell=\ell_{1} \ldots \ell_{n}\in\{0,1\}^n ℓ=ℓ1​…ℓn​∈{0,1}n，Kronecker’s delta可写成：${\delta }_{i\ell }={\prod }_{j=1}^n{\delta }_{i_j{\ell }_j}$；所以要证明的命题可等价转换为：${\prod }_{i=0}^{N-1}{c}_i^{{\prod }_{j=1}^n{\delta }_{i_j{\ell }_j}}$是一个0的承诺。

Prover：

• 计算bits ${\ell }_1\dots {\ell }_n$的承诺$c_{{\ell }_1},\dots ,c_{{\ell }_n}$。运行n个平行的$\Sigma$-Protocol for Commitment ℓ j ∈ { 0 , 1 } \ell_j\in\{0,1\} ℓj​∈{0,1}（上一节）
• 在其中任一个$\Sigma$-Protocol for ℓ j ∈ { 0 , 1 } \ell_j\in\{0,1\} ℓj​∈{0,1}，Prover：
  - 展示$f_1,\dots ,f_n$ 以形式：$f_j={\ell }_{j}x+a_j$
  - 令$f_{j,1}=f_j={\ell }_{j}x+a_j={\delta }_{1{\ell }_j}x+a_j$，$f_{j,0}=x-f_j=\left(1-{\ell }_j\right)x-a_j={\delta }_{0{\ell }_j}x-a_j$
  - 则对每个$i$，连乘积${\prod }_{j=1}^n{f}_{j,i_j}$是一个如下形式的多项式：
  $$p_i(x)=\prod _{j=1}^n\left({\delta }_{i_j{\ell }_j}x\right)+\sum _{k=0}^{n-1}{p}_{i,k}{x}^k={\delta }_{i\ell }{x}^n+\sum _{k=0}^{n-1}{p}_{i,k}{x}^k$$
• 现在的想法是，在初始消息中的prover将发送承诺$c_{d_0},\dots ,c_{d_{n-1}}$，该承诺将被用来抵消对应于$x^0,\dots ,x^{n-1}$的低阶系数.同时$x^n$的高阶系数将保证承诺$c_{\ell }$可以打开为0。Verifer最后将查验：
  $$\prod _{i=0}^{N-1}{c}_i^{{\prod }_{j=1}^n{f}_{j,i_j}}\cdot \prod _{k=0}^{n-1}{c}_{d_k}^{-x^k}$$
  是一个0的承诺。（根据Schwartz-Zippel lemma，除非$c_{\ell }$是0的承诺，否则成立的概率可以忽略。补充说明）

完整协议：

分析：
（黄色划线：证明for all $j$，$c_{{\ell }_j}$是0,1的承诺）$c_{{\ell }_j},c_{a_j},c_{b_j}$分别对应于上一节中的$c,a,b$，协议用于证明${\ell }_j\in 0,1$；经过$n$轮协议，可证明index $\ell <2^n$，范围合法。
（蓝色划线：证明$c_{\ell }={\mathrm{Com}}_{ck}\left(0;r\right)$）$c_{d_k}$
$$\begin{array}{rl}& \prod _i{c}_i^{{\prod }_{j=1}^n{f}_{j,i_j}}\cdot \prod _{k=0}^{n-1}{c}_{d_k}^{-x^k}\\ =& \prod _i{c}_i^{{\delta }_{i\ell }{x}^n+{\sum }_{k=0}^{n-1}{p}_{i,k}{x}^k}\cdot \prod _{k=0}^{n-1}{\left(\prod _i{c}_i^{p_{i,k}}{\mathrm{Com}}_{ck}\left(0;{\rho }_k\right)\right)}^{-x^k}\\ =& \prod _i\left(c_i^{{\delta }_{i\ell }{x}^n}\cdot c_i^{{\sum }_{k=0}^{n-1}{p}_{i,k}{x}^k}\cdot c_i^{-{\sum }_{k=0}^{n-1}{p}_{i,k}{x}^k}\right)\cdot \prod _{k=0}^{n-1}{\mathrm{Com}}_{ck}{\left(0;{\rho }_k\right)}^{-x^k}\\ =& c_{\ell }^{x^n}\cdot \prod _{k=0}^{n-1}{\mathrm{Com}}_{ck}\left(0;-{\rho }_k{x}^k\right)\\ (onlyif{c}_{\ell }={\mathrm{Com}}_{ck}\left(0;r\right))=& {\mathrm{Com}}_{ck}\left(0;r{x}^n\right)\cdot {\mathrm{Com}}_{ck}\left(0;-\sum _{k=0}^{n-1}{\rho }_k{x}^k\right)\\ =& {\mathrm{Com}}_{ck}\left(0;z_d\right)\end{array}$$

Ring Signature

思路：
结合两种技术：同态承诺+$\Sigma$-Protocol for One-out-of-N Commitment Containing 0=对等组认证协议。

1. 生成承诺密钥$ck$作为setup，用户的vk是0的承诺$c$。
2. 用$\Sigma$-协议证明用户知道其中一个承诺的打开。
3. 用Fiat-Shamir heuristic 变成非交互协议。

环签名：

Zerocoin

Zerocoin允许用户生成自己的硬币，这些硬币被列入在公告板上，通过公众共识变得有价值。然后，这些硬币可以匿名消费，而每枚硬币中都有一个秘密序列号，在消费协议中会显示出来，从而防止了双重消费。
零币协议的算法：(Setup, Mint, Spend, Vfy)

• $pp\leftarrow \mathrm{Setup}\left(1^{\lambda }\right)$
• $(c,skc)\leftarrow \mathrm{Mint}(pp)$ 铸币算法；输出硬币$c$和用于授权它支出的密钥$skc$
• $(\pi ,S)\leftarrow {\mathrm{Spend}}_{pp,skc}(M,c,C)$ 生成硬币用于支付交易的证明；输入交易串 M ∈ { 0 , 1 } ∗ M\in\{0,1\}^* M∈{0,1}∗（用来表示交易接收者的身份或合同条款），任意一组包含$c$的硬币$C$；输出证明$\pi$和一个序列号$S$
• $b\leftarrow {\mathrm{Vfy}}_{pp}(M,S,C,\pi )$ 验证支出交易的证明$\pi$。

Zerocoin 协议

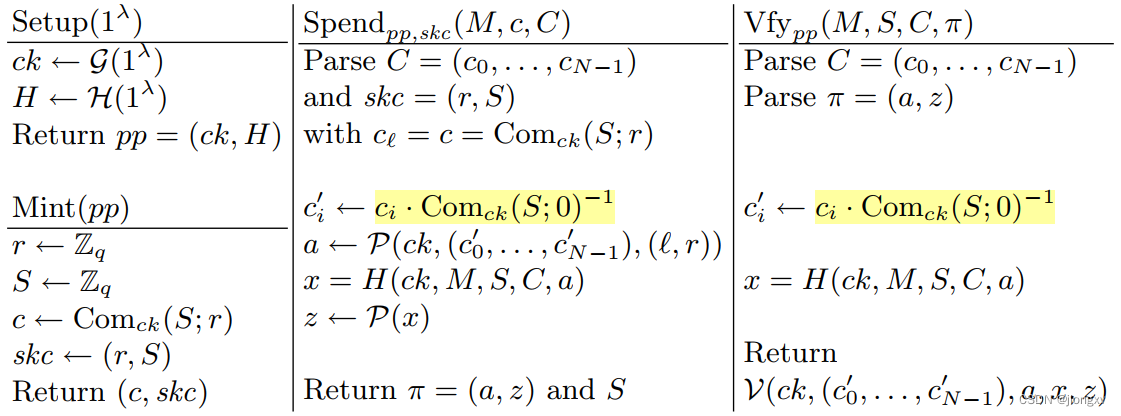
注意交易中被承诺的是序列号$S$不是0，所以在提交证明前先用${\mathrm{Com}}_{ck}(S;0{)}^{-1}$将所有承诺变成0的承诺。