论文笔记：Quotable Signatures using Merkle Trees

本文链接：https://blog.csdn.net/jiongxv/article/details/128715183

文章提出了使用Merkle树构建的引用签名方法来验证社交媒体上的新闻真实性，特别是针对假新闻问题。签名者通过对Merkle树根节点签名，而引用者只需提供验证路径来确认引用内容的真实性。计算成本分析表明，签名者和引用者需承担一定的计算负担，但可以通过选择高效的哈希和签名算法（如ECC）来降低开销。该方法能有效验证文本引用，而不必发布整个原始文本。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

https://dl.gi.de/handle/20.500.12116/25015

阅读文献：Kreutzer, M., Niederhagen, R., Shrishak, K. & Fhom, H. S., (2019). Quotable Signatures using Merkle Trees. In: David, K., Geihs, K., Lange, M. & Stumme, G. (Hrsg.), INFORMATIK 2019: 50 Jahre Gesellschaft für Informatik – Informatik für Gesellschaft. Bonn: Gesellschaft für Informatik e.V… (S. 473-477). DOI: 10.18420/inf2019_64

动机

通过使用Merkle树引用签名来验证社交媒体网站上分享的新闻，以解决假新闻的问题。

Fake News Detection

可引用签名，它对整个文本（message）有效，也对文本的部分引用（quote）有效：使用Merkle树，输入文本被分割成单个单词和标点。这些符号（tokens）的散列就是Merkle树的叶子。
这些叶节点上的默克尔树是二叉哈希树。每一层的节点都是上一层节点的成对哈希。
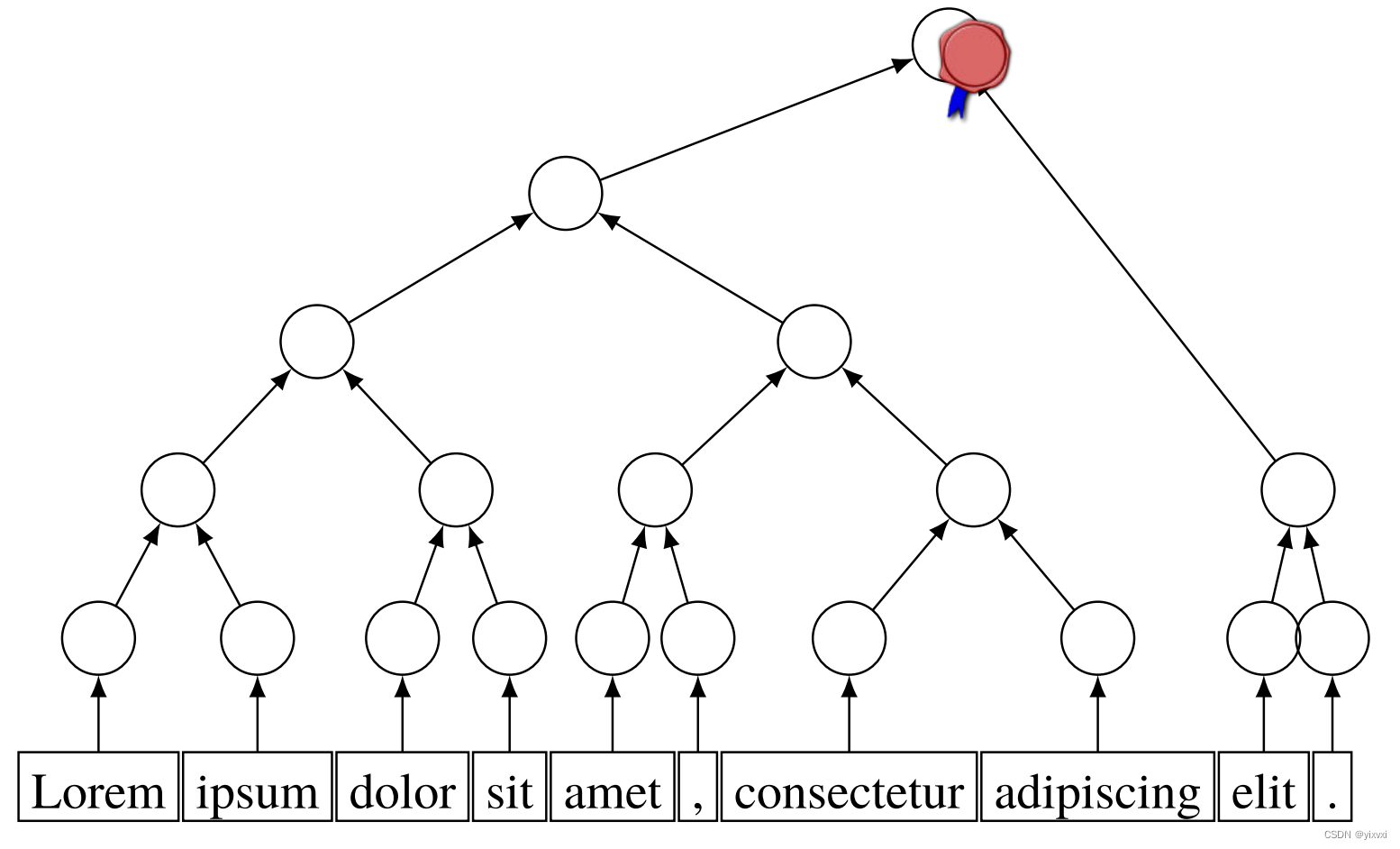
在这里插入图片描述
为了计算一个可引用签名，计算Merkle树直到根节点，并用私钥对这个根（root）进行签名。通过重新计算Merkle树的根并验证根上的签名。

在引用一篇文章时，自然只提供原文的一小部分。因此，并不是Merkle树的所有叶节点都可用，验证者需要额外的信息来计算根节点，从而验证签名。但是，不需要提供整个文本，只需要提供Merkle树中的验证路径就足够了，也就是说，树中从引用文本节点到根节点的路径上缺少的那些节点（如图灰色节点）。
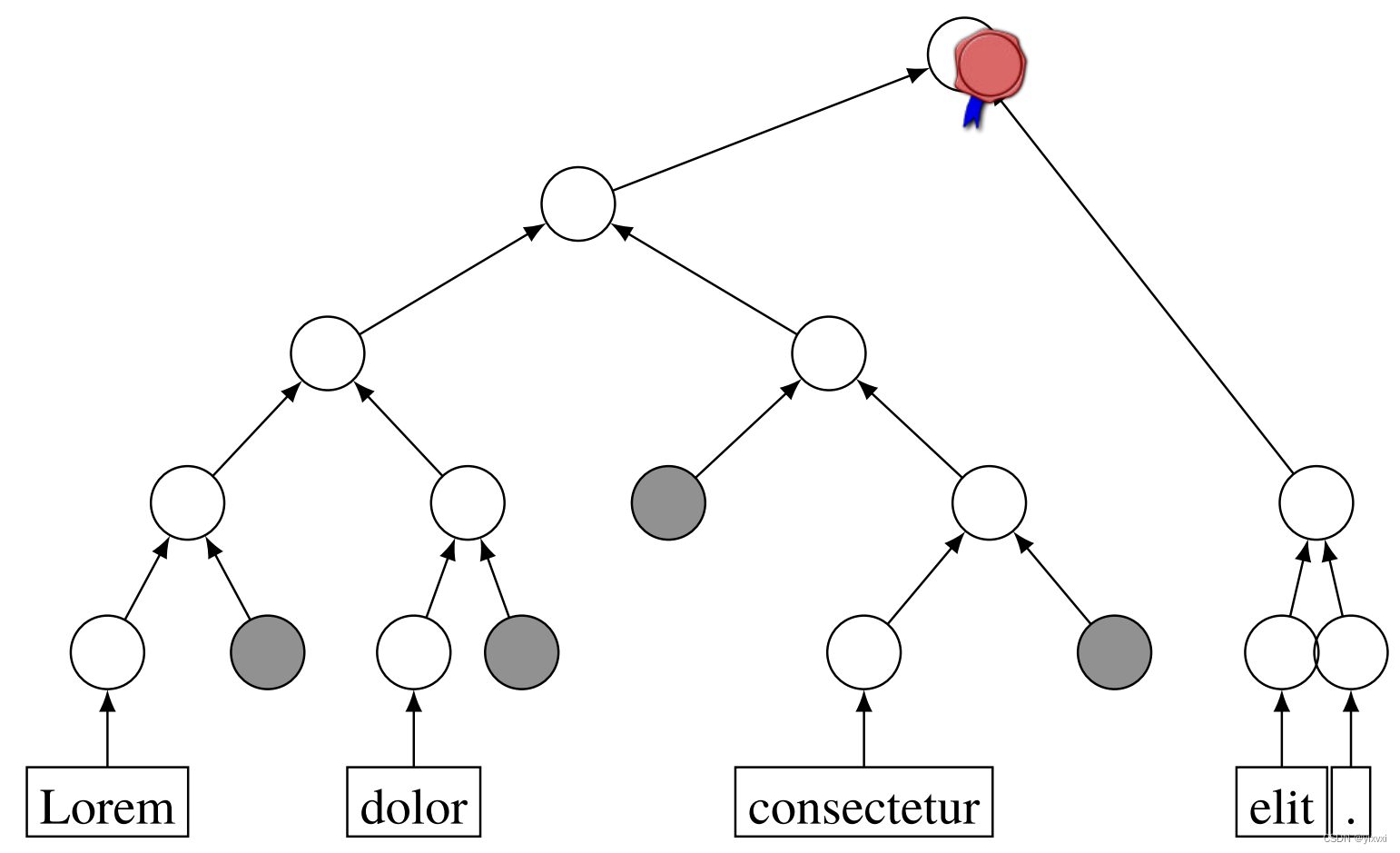
在这里插入图片描述
叶节点被计算为文本标记的散列。内部节点被计算为其子节点的连接值的哈希值。由于Merkle树的结构，验证者知道引用的文本中缺少哪些叶节点，因此拥有引用在哪里跳过原始文本的部分以及上下文可能在哪里缺失的信息

Cost

Signer
签名者的计算开销包括Merkle树的计算和根节点上签名的生成。

对于 $n$ 个标记的文本，树的高度为 $h = ⌈ l o g (n)⌉$ 。
有 $2^h−1$ 个内部节点需要从它们的子节点和 $n$ 个叶节点(文本标记的哈希)连接哈希。
因此，签名者总共必须计算 $2^h + n−1$ 次对哈希函数的调用，加上根节点上签名的计算。
Merkel树不需要发布,除了原始文本外，只需要根节点上的签名。根据验证方案，还需要其他信息。

Quoter
引用者的成本取决于引用的字数和引用的节数。为了估计最坏的情况成本，请考虑以下三种情况:

引用了一个单词:需要提供从叶节点到顶部的整个验证路径。因此，验证者必须重新计算整个默克尔树，即 $2^h + n−1$ 哈希值。需要提供 $h$ 个节点的整个验证路径;数据大小以 $h$ 哈希值增长。
文本中有一个连续的部分被引用:确切的代价取决于引用的令牌的数量。最坏的情况是Merkle树中间有两个单词的引用，需要独立的验证路径，几乎一直到根节点。在这种情况下，引用者需要计算 $2^h−1−2⌈log2(n/2)⌉$ 哈希值。验证路径下的节点数为 $2 ⌈ l o g 2 (n /2)⌉$ 。
引用了几个部分:引用的tokens越多，需要在Merkle树中重新计算的节点数量就越少。但是，对于验证路径的数据大小来说，最糟糕的情况是每两个单词都被引用。这要求验证路径上有 $n /2$ 个节点。(在这种情况下，提供原始tokens而不是它们的散列更有效。)因此，关于计算成本的最坏情况是重新计算几乎整个Merkle，即 $2^h−1−⌈log2(n)⌉$ 散列。

Verifier
在最坏的情况下，验证者需要重新计算有 $n$ 个叶子节点和 $2^h−1$ 个内部节点的整个树，这导致了 $2^h + n−1$ 次哈希函数调用的代价。验证路径中提供的节点越多，验证者路径需要重新计算的哈希值就越少。在任何情况下，验证者都需要验证根节点上的签名和签名者的certificate。

Statistics and Efficiency

1951年，香农声称英语文本的平均单词长度为4.5个字符[Sh51]。最近的研究表明，在现代文本中，平均单词长度略大。所以使用4个字符作为最坏情况估计的下限。

对于256-bit哈希函数，每个256位(32字节)哈希值对应ASCII编码中的32个字符。然而，为了将可引用签名嵌入HTML代码中，需要将哈希值编码为文本。为了兼容性，研究了Base64编码。在Base64编码中，每个256位字符串需要44个字符，等于44/4 = 11个tokens。换句话说，每个哈希值相当于11个存储令牌。因此，高度不超过4的子树可能用单词表示更好，而不是哈希。

假设单一，连续的引用，最坏情况下验证路径长度为 $2 ⌈ l o g 2 (n /2)⌉$ 。因此，对于24个tokens，最坏情况签名等于文本的长度: $24·4 = 96 = 2·⌈log_2(12)⌉·11 + 2·4$ 。因此，可引用签名的最小文本大小约为24个标记或约96个字符。