【算法专题】置换群——burnside引理、polya定理

今天朋友问我一道题

一条含有N个珠子的项链，每个珠子都有t种不同的染色。旋转、翻折后相同的项链视为
一种。问有多少本质不同的项链。

想起高中学数学竞赛看《奥赛经典》群置换时遇到过相似的题，遂复习了一下，学习了burnside引理和polya定理，收获颇丰。

先总结一下burnside引理和polya定理应用场景（我遇到的）

经过置换（翻折、旋转）可视为同一种情形下的求染色方案数问题

网上看到一个介绍burnside引理和polya定理的博客，写的通俗易懂：
（链接https://blog.csdn.net/liangzhaoyang1/article/details/72639208）




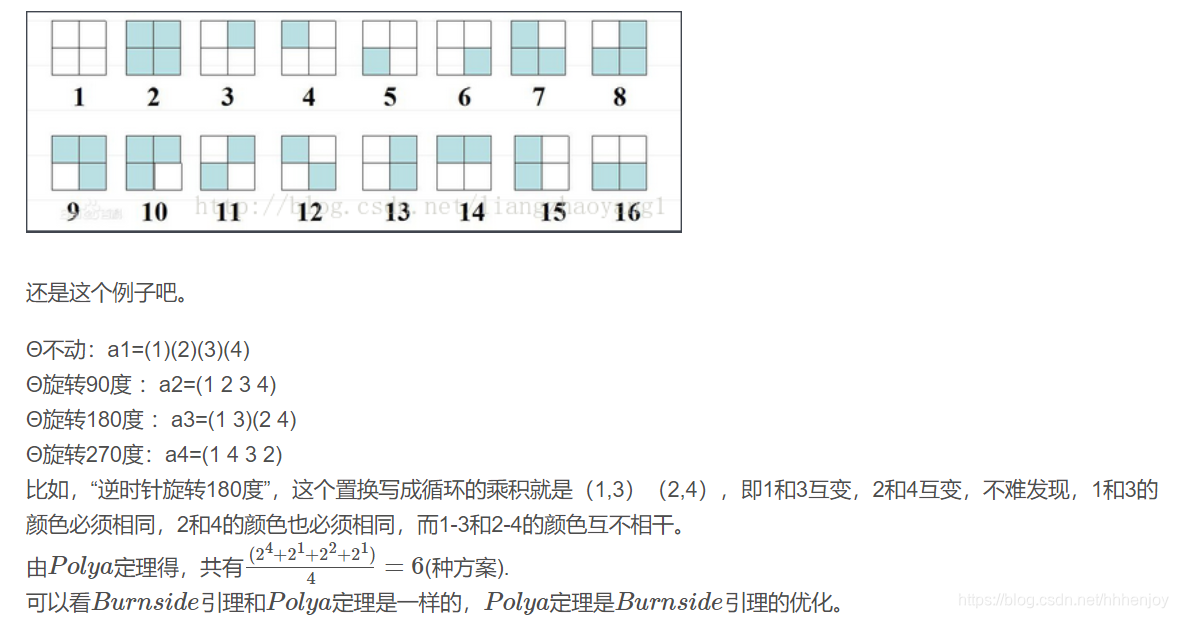
其他例题：
HDOJ：2084、2647、1812、3411、2865、2481
POJ：1286、2409、2154、2888