算法学习笔记五 斐波那契数列

斐波那契数列

一、最基本的

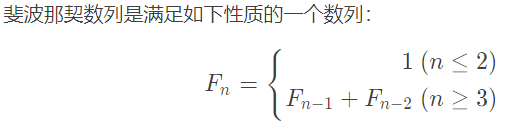
所以，只要知道这个数列的前两项，就可以求出之后所有项了。
核心部分（最简单的递推方法，但是范围是n<=48，否则会超时and溢出）：

#include <cstdio> //头文件
int main()
{
    double f[50];
    int n, i;
    f[0] = 0;   //其实并没有用

    f[1] = 1;
    f[2] = 1;   //两个初始值

    scanf_s("%d", &n);
    for (i = 3; i <= n; i++)
        f[i] = f[i - 1] + f[i - 2];  //开始使用斐波那契数列

    printf("%0.2lf", f[n]); //输出，保留两位小数
    return 0;
}

【注意，这种简单方法还有一种表示，就是用函数写，把递推式变成函数的递归调用，也很好理解。但是亲测会比递推式的时间长很多，n>35的时候就TLA了。因此这提示我们，函数的递归是很耗时的，不要多用。同时上述方法比较快的一个原因是用数组储存时，许多已经算过的数就不用算了，当然会快很多】

二、快速做法（矩阵乘法+快速幂 ）

矩阵乘法推导

$$F_i=F_{i-1}+F_{i-2}$$
$$F_{i-1}=F_{i-1}+0$$

把两个式子转化为矩阵形式，即（都是2x2的方便写代码）
$$\left\{\begin{array}{cc}{F}_i& 0\\ F_{i-1}& 0\end{array}\right\}=\left\{\begin{array}{cc}1& 1\\ 1& 0\end{array}\right\}\ast \left\{\begin{array}{cc}{F}_{i-1}& 0\\ F_{i-2}& 0\end{array}\right\}$$

$$\left\{\begin{array}{cc}{F}_{i-1}& 0\\ F_{i-2}& 0\end{array}\right\}=\left\{\begin{array}{cc}1& 1\\ 1& 0\end{array}\right\}\ast \left\{\begin{array}{cc}{F}_{i-2}& 0\\ F_{i-3}& 0\end{array}\right\}$$
…一直到

$$\left\{\begin{array}{cc}{F}_3& 0\\ F_2& 0\end{array}\right\}=\left\{\begin{array}{cc}1& 1\\ 1& 0\end{array}\right\}\ast \left\{\begin{array}{cc}{F}_2& 0\\ F_1& 0\end{array}\right\}$$

总结即
$$\left\{\begin{array}{cc}{F}_i& 0\\ F_{i-1}& 0\end{array}\right\}={\left\{\begin{array}{cc}1& 1\\ 1& 0\end{array}\right\}}^{(i-2)}\ast \left\{\begin{array}{cc}{F}_2& 0\\ F_1& 0\end{array}\right\}$$

即
$$\left\{\begin{array}{cc}{F}_i& 0\\ F_{i-1}& 0\end{array}\right\}={\left\{\begin{array}{cc}1& 1\\ 1& 0\end{array}\right\}}^{(i-2)}\ast \left\{\begin{array}{cc}1& 0\\ 1& 0\end{array}\right\}$$

基于此方法，可以看到我们要求的就是一个矩阵的i-2次幂即可，然后$F_i$就等于结果再乘以一个[1 0 ，1 0] 的第 [0][0] 个元素。

而求幂，我们可以采用快速幂的方法：

快速幂

快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。

戳下面链接理解快速幂原理：
快速幂算法 刘杨俊

//base为底数，power为指数，求结果的后三位（求后三位就对结果对1000取模即可）
#include<iostream>
using namespace std;

long long fastPower(long long base, long long power) 
{
    long long result = 1;
    while (power > 0) 
    {
        if (power % 2 == 1)
            //如果指数为奇数
            result = result * base % 1000;//相当于结果里已经乘过一次被分离出来的底数了
        power = power / 2;    //不管对于奇数/偶数，除以2就是整数
        base = base * base % 1000;    //指数除2，则底数平方
        cout << "base:" << base << "power:" << power << endl;
    }
return result;
}

int main() {
    int base, power;
    cin >> base >> power;
    cout << fastPower(base, power);
    return 0;
}

运行结果：

矩阵快速幂

首先矩阵乘法的模板长这样，还是很好理解的：

int main()
{
	int a[110][110] = {};
	int b[110][110] = {};
	int c[110][110] = {};

	int n = 0, m = 0, p = 0;
	cin >> n >> m;//矩阵a为n*m（n行m列） 
	for (int i = 0; i < n; i++)    //一行一行地输入
		for (int j = 0; j < m; j++)
			scanf("%d", &a[i][j]);

	cin >> p;  //矩阵b为m*p（m行p列）
	for (int i = 0; i < m; i++)
		for (int j = 0; j < p; j++)
			scanf("%d", &b[i][j]);


//重点在这里
	for (int i = 0; i < n; i++)   //矩阵c是a与b相乘得到的 
		for (int j = 0; j < p; j++) //n*p（n行p列） 
			for (int k = 0; k < m; k++)
				c[i][j] += a[i][k] * b[k][j];    //注意是求多项的和，是+=

	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < p; j++)
			cout << c[i][j] << " ";
		cout << endl;
	}
	return 0;
}

矩阵快速幂即对矩阵使用快速幂的思想，既然求幂了就说明这是个方阵，设为NxN，对于方阵的乘法就要简洁很多：

#include <bits/stdc++.h>

using namespace std;

struct Matrix {
	long long a[N][N];
};   //定义一个结构，方便作为返回值，并且进行重载运算符，不然要写很多次函数hhh

Matrix operator * (Matrix a, Matrix b) {   
    //重载对Matrix类型变量的运算符*（乘号），就是写的一个乘法，a和b都是NxN的方阵
    Matrix ans;
    memset(ans.a, 0, sizeof(ans.a));   //初始化为0
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            for (int k = 0; k < N; k++)
                ans.a[i][j] += a.a[i][k] * b.a[k][j];
    return ans;
}

矩阵快速幂：把快速幂的思想应用于矩阵的方阵乘法【这里就是快速幂的核心了，和前面实数是一样的，如果指数是奇数则把底数y取出来，如果是偶数就使底数平方，指数-1…】

Matrix power(Matrix a, int p) {    //对a求p次幂的函数
	Matrix y = a, k = a;   //y是一个中间变量，k是结果
	int t = p;
	while (t) {
		if (t & 1) k = k * y;   //t&1，若t为奇数，则结果为1！
		y = y * y;
		t >>= 1;   //t-1的高端写法！
	}
	return k;
}

完整代码

把矩阵快速幂应用于斐波那契数列：
$$\left\{\begin{array}{cc}{F}_i& 0\\ F_{i-1}& 0\end{array}\right\}={\left\{\begin{array}{cc}1& 1\\ 1& 0\end{array}\right\}}^{(i-2)}\ast \left\{\begin{array}{cc}1& 0\\ 1& 0\end{array}\right\}$$
就是，当求Fn的时候，只要求[1 1 ,1 0]的n-2次幂乘以[1 0 , 1 0]：

//所有数字的定义一定要记得是long long......血的教训

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;

const int N = 3;
const long long mod = 1000000007;   //一般结果都很大！要取模

struct Matrix {
	long long out[N][N];
};   //定义一个结构，方便作为返回值，并且进行重载运算符，不然要写很多次函数hhh

Matrix operator * (Matrix a, Matrix b) {
	//重载对Matrix类型变量的运算符*（乘号），就是写的一个乘法，a和b都是NxN的方阵
	Matrix ans;
	memset(ans.out, 0, sizeof(ans.out));   //初始化为0
	for (int i = 1; i < N; i++)
		for (int j = 1; j < N; j++)
			for (int k = 1; k < N; k++)
				ans.out[i][j] = ans.out[i][j] + (a.out[i][k] * b.out[k][j]) % mod;
	return ans;
}

Matrix power(long long p) {    //对底数求p次幂的函数
	Matrix base;
	base.out[1][1] = 1;
	base.out[1][2] = 1;
	base.out[2][1] = 1;
	base.out[2][2] = 0;
	Matrix ans;
	ans.out[1][1] = 1;
	ans.out[1][2] = 0;
	ans.out[2][1] = 0;
	ans.out[2][2] = 1;
	long long t = p;
	while (t > 0) {
		if (t & 1)   //t&1，若t为奇数，则结果为1！
		{
			Matrix tmp = ans * base;
			for (int i = 1; i < N; i++)
				for (int j = 1; j < N; j++)
					ans.out[i][j] = tmp.out[i][j];
		}
		Matrix tmp = base * base;
		for (int i = 1; i < N; i++)
			for (int j = 1; j < N; j++)
				base.out[i][j] = tmp.out[i][j];
		t >>= 1;   //t-1的高端写法！
	}
	return ans;
}

int main() {
	long long n;
	cin >> n;
	n = n - 2;
	if (n == 1 || n == 2)
	{
		cout << 1;
		return 0;
	}
	Matrix result = power(n);
	long long feib = (result.out[1][1]+result.out[1][2]) % mod;
	printf("%lld\n", feib);
	return 0;
}

三、理论表达式

有这么一道题目很有意思的题：

---

---

如果不熟悉斐波那契数列可能还需要花费一些时间…所以在这里把这一点列出来，只要看出了这道题的本质就是求斐波那契数列，就非常的简单了。

---

（摘自洛谷 密期望的题解）

---