3.3 MATLAB学习笔记之矩阵处理-矩阵求值

最新推荐文章于 2024-10-09 10:21:40 发布

难得迷虎

最新推荐文章于 2024-10-09 10:21:40 发布

阅读量228

点赞数 2

文章标签： matlab 学习笔记

本文链接：https://blog.csdn.net/jjh1203god/article/details/142779442

版权

矩阵求值

矩阵求值是指对一个矩阵进行某种运算，其结果是一个数值，包括求矩阵的行列式值、秩、迹、范数、条件数等。

一、方阵的行列式

把一个方阵看做一个行列式，并对其按行列式的规则求值，这个值就称为矩阵所对应的行列式的值。在MATLAB中，求方阵A所对应的行列式的值的函数是**det(A)**。

A =

    0.8147    0.6324    0.9575    0.9572
    0.9058    0.0975    0.9649    0.4854
    0.1270    0.2785    0.1576    0.8003
    0.9134    0.5469    0.9706    0.1419

>> B=det(A)

B =

   -0.0261

二、矩阵的秩与迹

1矩阵的秩

矩阵线性无关的行数与列数称为矩阵的秩。

什么叫矩阵线性无关的行与列呢?

事实上，一个m×n矩阵A是由m个行向量组成或由n个列向量组成的。通常，对于一组向量x₁,x₂, … ,xp,若存在一组不全为零的数ki(i=1,2, … ,p), 使
$k_{1}x_{1}+k_{12}x_{2}+…+k_{p}x_{p}=0$
成立，则称这p个向量线性相关，否则称线性无关

对于m×n矩阵A,若m个行向量中有r(r≤m)个行向量线性无关，而其余为线性相关，称r为矩阵A的行秩；类似地可定义矩阵A的列秩。

矩阵的行秩和列秩必定相等，将行秩和列秩统称为矩阵的秩，有时也称为该矩阵的奇异值数。

在MATLAB中，求矩阵秩的函数是**rank(A)**。

>> A=[2,2,-1,1;4,3,-1,2;8,5,-3,4;3,3,-2,2]

A =

     2     2    -1     1
     4     3    -1     2
     8     5    -3     4
     3     3    -2     2

>> r=rank(A)

r =

     4

2矩阵的迹

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。

在MATLAB中，求矩阵的迹的函数是**trace(A)**。

>> A=[2,2,3;4,5,-6;7,8,9]

A =

     2     2     3
     4     5    -6
     7     8     9

>> trace(A)

ans =

    16

三、矩阵或向量的范数

矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。

范数有多种方法定义，其定义不同，范数值也就不同，因此，讨论向量和矩阵的范数时，一定要弄清是求哪一种范数。

1.向量的3种常用范数

设向量V=(v1,v2,…,vn),它的3种范数定义如下。

(1)向量1-范数：向量元素的绝对值之和。

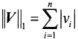
(2)向量2-范数：向量元素平方和的平方根。

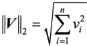
(3)向量∞-范数：所有向量元素绝对值中的最大值。

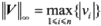
在MATLAB中，求这3种向量范数的函数如下：

norm(V,1)

norm(V)或norm(V,2)

norm(V,inf)

其中，V是向量。3种格式的函数分别计算V的1-范数、2-范数和∞-范数。

>> V=[-1,1/2,1]

V =

   -1.0000    0.5000    1.0000

>> vl=norm(V,1)

vl =

    2.5000

>> v2=norm(V)

v2 =

    1.5000

>> v3=norm(V,inf)

v3 =

     1

2.矩阵的范数

设A是一个m×n矩阵，V是一个含有n个元素的列向量，矩阵A的范数可以定义为
$∣∣ A ∣∣ = ma x ∣∣ A \cdot V ∣∣, ∣∣ V ∣∣ = 1$
因为A是一个m×n矩阵，而V是一个含有n个元素的列向量，所以A·V是一个含有m个元素的列向量。

在前面已经定义了3种不同的向量范数，按照上式也可以定义3种矩阵范数，这样定义的矩阵范数||A||称为A 从属于向量的范数。

上式只给出了矩阵范数的基本定义，未给出具体计算方法，完全按照上式是难以计算一个矩阵的某种具体范数的。从属于3种向量范数的矩阵范数计算公式如下。

(1)矩阵A的1-范数：所有矩阵列元素绝对值之和的最大值。

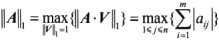
(2)矩阵A 的2-范数：A’A 矩阵的最大特征值的平方根。

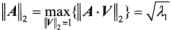
其中，λ1为A’A的最大特征值。

(3)矩阵A 的 ∞- 范数：所有矩阵行元素绝对值之和的最大值。

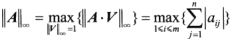
MATLAB 提供了求3种矩阵范数的函数，其函数调用格式与求向量的范数的函数完全相同。例如：

>> A=[1,0,1,0,5;3,5,7,4,6]

A =

     1     0     1     0     5
     3     5     7     4     6

>> al=norm(A,1)

al =

    11

>> a2=norm(A)

a2 =

   12.1738

>> a3=norm(A,inf)

a3 =

    25

四、矩阵的条件数★★

在求解线性方程组AX=b时，一般认为，系数矩阵A中个别元素的微小扰动不会引起解向量的很大变化。这样的假设在工程应用中非常重要，因为一般系数矩阵的数据是由实验数据获得的，并非精确值，但与精确值误差不大。

由上面的假设可以得出结论：当参与运算的系数与实际精确值误差很小时，所获得的解与问题的准确解误差也很小。遗憾的是，上述假设并非总是正确的。

对于有的系数矩阵，个别元素的微小扰动会引起解的很大变化，在计算数学中，称这种矩阵为病态矩阵，而称解不因其系数矩阵的微小扰动而发生大的变化的矩阵为良性矩阵。

当然，良性与病态是相对的，需要一个参数来描述，条件数就是用来描述矩阵的这种性能的一个参数。

**矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积，**即
$cond(A)=||A|| · ||A^{-1}||$
这样定义的条件数总是大于1的。条件数越接近于1,矩阵的性能越好，反之，矩阵的性能越差。

A 有3种范数，相应地可以定义3种条件数。在MATLAB中，计算A 的3种条件数的函数如下：

(1)cond(A,1): 计算A的1-范数下的条件数。
$cond(A,1)=||A||_1 · ||A^{-1}||_1$
(2)cond(A) 或**cond(A,2): 计算A 的2-范数下的条件数。
$cond(A)=||A||_2 · ||A^{-1}||_2$
(3)cond(A,inf)**:计算A 的∞-范数下的条件数。
$cond(A,inf)=||A||_∞ · ||A^{-1}||_∞$

>> A=[2,2,3;4,5,-6;7,8,9]

A =

     2     2     3
     4     5    -6
     7     8     9

>> c1=cond(A)

c1 =

   87.9754

>> B=[2,-5,4;1,5,-2;-1,2,4]

B =

     2    -5     4
     1     5    -2
    -1     2     4

>> c2=cond(B)

c2 =

    3.7515