集合问题 : 容斥原理

容斥原理用于解决有交集的集合的组合问题
$\\$
其实这种思想很多人不用学便以及在运用了, 很简单的一个东西

举个例子 :

有三个集合 : 棕,红,黄,绿 , 其中棕包含所有其他三个集合 , 求除去其他三个集合后的棕集合

设 : 棕,红,黄,绿集合为$A,A_1,A_2,A_3,$那么答案便是 :

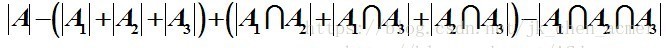
1. 颜色为红黄绿的部分就不说了 , 自然减去一次即可
2. 颜色为蓝的部分在减去$|A_1|+|A_2|+|A_3|$的时候被减掉两次,所以加回一次
3. 黑色的部分减$|A_1|+|A_2|+|A_3|$时减去三次,又在加$|A_1∩A_2|+|A_2∩A_3|+|A_1∩A_3|$时加上三次,所以还得减去一次

$\\$

---

$\\$

在比赛中, 容斥原理用到的地方特别多, 比如, 和gcd有关的求方案数问题, 排列组合的问题, 序列问题 , 涂色问题

顺手摸出几道题的题解 :

区间内gcd为 i 的对数
预处理所有数的因子数

---

涂色问题

n朵花一排, 有m种颜色, 涂色不能有相邻花同种颜色, 问恰好使用k种颜色的方案数

首先是选出k种颜色, $C_{m}^k$

如果k种颜色直接去涂的结果为$k*(k-1)^{n-1}$, 但是这样只保证相邻花色不同, 却不能保证恰好使用k种颜色

分析一下怎么转换成刚好k种颜色 $\\$ k种颜色直接涂包含了使用k种颜色的情况, 却多包含了使用不到k种的情况, 所以我们要把这些情况容斥掉 $\\$ 设直接涂x种的方案数为$A_x=C_k^x*x*(x-1)^{n-1}$ $\\$ 那么是不是觉得和上面那三个圆一样 $$\therefore ans=C_m^k*(A_k-A_{k-1}+A_{k-2}...+(-1)^kA_0)$$