变量间关系的度量
一、变量间的关系
变量间的关系形态可分为两种类型:函数关系、相关关系。
函数关系:一 一对应的确定关系。
相关关系:变量之间存在的不确定的数量关系,即 一个变量的取值不能由另一个变量唯一确定。
二、相关关系的描述与测度
相关分析是对两个变量之间线性关系的描述与度量,解决的问题
1、如果存在关系,它们之间是什么样的关系?
2、变量之间的关系强度如何?
3、样本所反映的变量之间的关系能否代表总体变量之间的关系?
步骤如下:
绘制散点图来判断变量之间的关系形态,如果是线性关系,利用相关系数测度两个变量之间的关系强度,最后对相关系数进行显著性检验,以判断样本所反应的关系能否用来代表两个变量总体上的关系。
(一)散点图
散点图:用坐标的水平轴代表自变量X,纵轴代表因变量Y,每组数据在坐标系中用一个点表示,n组数据在坐标系中形成的n个点称为散点,由坐标及散点形成的二维数据坐标图。
散点图描述了两个变量之间的大致关系形态以及关系强度。
如果变量之间的关系近似地表现为一条直线,称线性相关
如果变量之间的关系近似地表现为一条曲线,称非线性或者曲线相关
如果两个变量的观测点狠分散,无任何规则,则表示变量之间没有相关关系
在线性相关中,两个变量的变动方向相同----正相关
在线性相关中,两个变量的变动方向相反----负相关
不同形态的散点图如下:
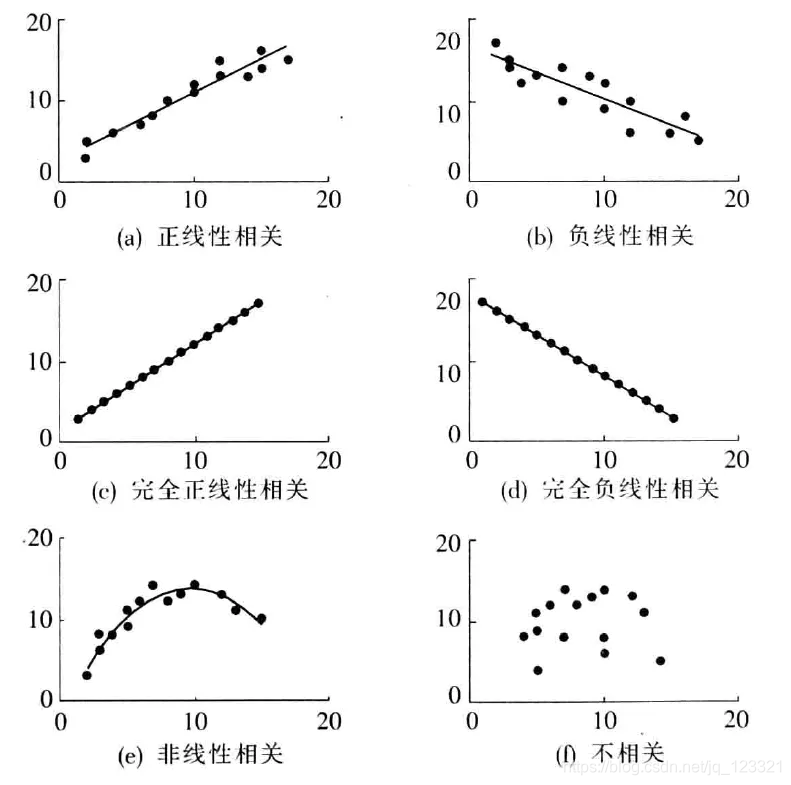
eg:不良贷款与以下因素是否有关,以及关系。

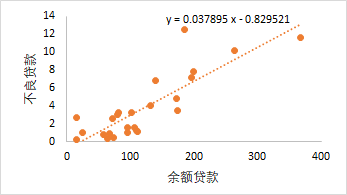


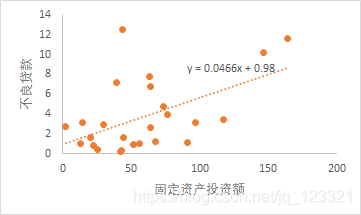
从以上的各散点图可知,不良贷款与贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间具有一定的线性相关。与贷款余额的线性关系比较密切。
(二)相关系数
为准确度量两个变量之间关系的密切程度,需计算相关系数
相关系数:根据样本数据计算的对两个变量之间线性关系强度的度量值,r表示。
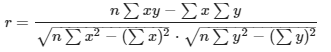








 本文介绍了变量间的关系类型,如函数关系和相关关系,重点讨论了相关关系的描述与测度,包括散点图和相关系数。相关系数的性质和显著性检验有助于理解变量间的线性关系。接着,文章深入探讨了一元线性回归分析,包括一元线性回归模型、最小二乘估计、拟合优度和显著性检验。最后,讨论了如何利用回归方程进行点估计和区间估计,为预测和控制提供依据。
本文介绍了变量间的关系类型,如函数关系和相关关系,重点讨论了相关关系的描述与测度,包括散点图和相关系数。相关系数的性质和显著性检验有助于理解变量间的线性关系。接着,文章深入探讨了一元线性回归分析,包括一元线性回归模型、最小二乘估计、拟合优度和显著性检验。最后,讨论了如何利用回归方程进行点估计和区间估计,为预测和控制提供依据。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








