DP——01背包问题使用迭代和动态规划（超详细——小白入门）

 

 

 

 

 

 题目：给定N个项目的权重和价值（利润），将这些项目放入最大容量W的背包中，以获得背包中的最大总值（利润）。 让我们简化问题陈述

假设我是一个小偷，到达某个地方抢劫，并且没有人在家。

我为了放置物品而拿的麻袋最多可以承重5公斤。我要偷东西最大利润是多少？(PS纯属虚构)

 

输入：

   int knapsackMaxWeight = 5;

   int profit []= {200,240,140,​​150};

   int weight []= {1，3，2，5};

 

输出：

通过选择权重为1和3的项目，我们得到的最大利润是440。

 

______________________________________________________________________________________________

 

递归算法：

 

 

解决这个问题的方法之一是尝试每一个重量的组合，直到它达到麻袋承重能力，看看在哪个组合中我们将获得最大的利润，包括检查利润

 

 

1.只有重量为1的项目（利润=200）

2.只有重量为3的项目（利润= 240）

3.只有重量为2的项目（利润= 140）

4.只有重量5（利润= 150）

5.只有重量1和3的组合（利润= 440）

6.只有重量3和2（利润= 380）等

 

 

此时我们由这个问题得到了一个子问题通用的解决方案，来检查我得到的利润

• 通过挑选项目
• 或不挑选该项目

这也就是选与不选的问题

 

 

当我选择物品时，我需要将其从计算中移除，因为您已经对当前物品进行了处理，并通过拾取物品的重量减少了背包容量。

 

当我不选择物品时，我需要从计算中删除它，因为你已经在当前物品上工作，并保持背包的容量，因为此时我们还没有选择物品。

 

下图就是动态递归地显示选与不选的图解

 

然后我们再来看一看这个过程中发生的递归过程(自下而上)

 

 

code如下：

 

 

#include<stdio.h>
int max(int a, int b) { return (a > b)? a : b; }

int knapSack(int W, int wt[], int val[], int n)
{

if (n == 0 || W == 0)
	return 0;


if (wt[n-1] > W)
	return knapSack(W, wt, val, n-1);


else return max( val[n-1] + knapSack(W-wt[n-1], wt, val, n-1),
					knapSack(W, wt, val, n-1)
				);
}


int main()
{
	int val[] = {200, 250, 140，150};
	int wt[] = {1, 3, 2,5};
	int W = 50;
	int n = sizeof(val)/sizeof(val[0]);
	printf("%d", knapSack(W, wt, val, n));
	return 0;
}

 

 

 

 

 

 

我们继续思考，联系我们学到的递归知识，这个程序其实是很低效的，因为它做了很多重复的计算，尝试每个组合的方法的问题是重复步骤，因为它存

在重叠的子问题。如果给定的项目weight和利润是，Weight [] = {1,1,1}，Profit [] = {30,40,50}，KnapSackMaxWeigth = 2，尝试为此创建

递归树，会看到一些像下面的东西，这种方法具有重复的计算和时间复杂性是指数的。（指数级别是由树的深度depth决定的）

 

 

 

动态规划方法

________________________________________________________________________________________________________

在这个方法中，我们将使用动态规划来解决问题。

我们将计算每种类型输入获得的利润，并存储每个计算的结果。

因此，只要在算法中进一步需要进行相同类型的输入计算，就不需要再次计算，直接参考之前的计算结果。

我们首先采取临时数组 k[] []的方式 

1. 行长度（我们有的项目数量）
2. 列长度​​（背包容量）

再来 严格数学定义

设F( i ,j )为最有价值的总集。可以把前i个物品放进能够承重为j的背包的子集分两个类别： 包括第i个物品的子集和不包括第i个物品的子集

有如下结论

（1）在不包括第i个物品的子集中,最优子集的价值是F(i-1,j);

  (2) 在包括第i个物品的子集中 （j-wi>=0），最优子集是由该物品和前i-1个物品所能够放进承重为j-wi的背包最优子集构成。这种最优子集的总价值为

vi+F(i-1,j-wi)；

 

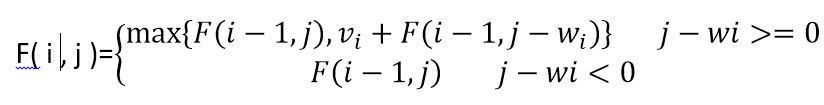
所以我们要做的是把问题分解成更小的问题，解决问题并存储结果。

 

 

一.考虑对weight=1操作

1.特殊情况：如果袋容量是0，我们将开始检查我们可以选择多少物品（让我们开始研究一个重量为1，口袋容量为0的物品。 如果我们的口袋容量为0，那么我们将无法挑选任何物品（如果我们有更多的物品(max0的一列)，我们仍然不能选择任何物品，因为袋子容量本身是0），所以对于容量为0的列，所有入口都是0，这意味着如果容量为0，则不能获得利润。

 

 

2.普适情况：

Max>=1时，有且只有一个最优解weight=1，所以这一列最大利润都是value=200；如图

 

二.考虑对weight=3操作

 

Max===【0-2】时

j-wi<0   两个项目可供选择，重量为1的项目和重量为3的项目。

3.1   现在，我们需要看看，我们可以添加重量为3的物品，以解决容量1,解决容量2 

j-wi<0,条件不成立,取F(i-1,j)=200;

 

3.2 现在，我们需要看看，我们可以添加重量为3的物品，以解决容量3的问题

我们要思考两个问题：

1.选择当前项目是重量为3的项目将给我们最大的利润

2.或者不选择当前项目将给我们最大的利润。

 

key:

选3；利润=240，剩余空间=0；

不选：利润=200；

Max(选, 不选) = Max(240, 200) = 240.

 

Max=【3-5】时

 

背包容量=3；

我们有重量1,3考虑（特别注意）

3<=3=TRUE;

 

如果我们放3，背包剩余0；

我们考虑——选了这个后+剩余和原来的比大小

最大利润：

Max(当前重量的价值+保留的重量的价值，不包含当前重量的价值[不参与选])

=Max([240+K[0][0]],[200])

=Max([240+(0),[200])

=Max(240,200)

=240;

 

这也意味着背包容量=3；1，和3可选，我们最大利润在取3时得到240 

 

背包容量为4

 

我们有重量1,3考虑 

3<=4=TRUE;

 

如果我们选择3，背包剩余4-3=1能做到最好的是；

最大利润：

Max(当前重量的价值+保留的重量的价值，不包含当前重量的价值[不参与选) j-wi>=0成立

=Max([240+K[0][1],[200])

=Max([240+(1),[200])

=Max(240+200,200)

=440;

问：200从哪里来？

这是当我们重量为1的时候得到的利润，我们已经计算出了当重量为1的时候利润为200，(已经存起来)

 

这也意味着背包容量=4；1，和3可选，我们最大利润在取1,3时得到440 

 

 

背包容量=5；

我们有重量1,3考虑

3<=5=TRUE;

 

如果我们放3，背包剩余5-3=2；

最大利润：

Max(当前重量+保留的重量，不包含当前重量)

=Max([3+K[1-1][5-3],[200])

=Max([240+200,[200])

=Max(240+200,200)

=440;

问：200从哪里来？

这是当我们重量为1的时候得到的利润，我们已经计算出了当重量为1的时候利润为200，(已经存起来) 

 

 

三.考虑对weight=2操作

 

Max===【0-1】时——————【详细分析在weight=2已经给出，这里不再赘述】

j-wi<0   直接有公式选得 F(i,j)=F(i-1,j)得。

 

Max=2

max(140+k[3-1][2-2],200)

=max(140+k[2][0],200)

=max(140,200)

=200;

 

Max=3

 

max(140+k[3-1][3-2],200)

=max(140+k[2][1],200)

=max(140+200,200)

=340;

 

Max=4

max(140+k[3-1][4-2],440) //思考这里为什么成了440？

=max(140+k[2][2],440)

=max(140+200,4400)

=440;

 

Max=5

max(140+k[3-1][5-2],440)

=max(140+k[2][3],440)

=max(140+200,440)

=440;

三. 考虑对weight=5操作

j-wi<0——————

【0-4】遵循F（i,j）= F(i-1,j),即上移一行的原则

Max=5

 

max(150+k[4-1][5-5],440)

=max(150+k[3][0],440)

=max(150+200,440)

=440;

这也意味着背包容量=5；1，3和2,5可选，我们最大利润得到440;

最优解得出：

 

 

 

c ode如下

#include<stdio.h>


int max(int a, int b) { return (a > b)? a : b; }

 
int knapSack(int W, int wt[], int val[], int n)
{
int i, w;
int K[n+1][W+1];


for (i = 0; i <= n; i++)
{
	for (w = 0; w <= W; w++)
	{
		if (i==0 || w==0)
			K[i][w] = 0;
		else if (wt[i-1] <= w)
				K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);
		else
				K[i][w] = K[i-1][w];
	}
}

return K[n][W];
}

int main()
{
	int val[] = {200, 250, 140，150};
	int wt[] = {1, 3, 2,5};
	int W = 5;
	int n = sizeof(val)/sizeof(val[0]);
	printf("%d", knapSack(W, wt, val, n));
	return 0;
}

——————————————————————————————————————————

问题讨论结束：留给我们的启迪应该是为什要发明出动态规划算法来解决这一类的问题？

 

把问题推演到我们熟悉的 斐波那契数列问题就一目了然

 

在前三个步骤中，可以清楚地看到fibo（n-3）被计算两次。如果进一步深入递归，可能会发现一再重复相同的子问题亿ji，如果数据量

大到以亿计算，计算的重复量就会巨大。

 

fibo(n) = fibo(n-1) + fibo(n-2)
ffibo(n-1) = fibo(n-2) + fibo(n-3)
fibo(n-2) = fibo(n-3) + ffibo(n-4)
.................................
................................
................................
fibo(2) = fibo(1) + fibo(0)

 

 

DP优于递归的好处：

动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再合并子问题的解以得出原问题的解。

通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化

存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增速时特别有用。(维基百科)